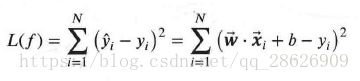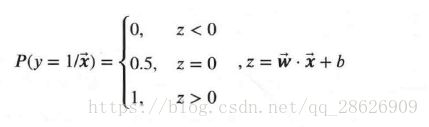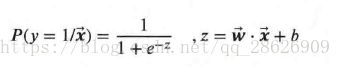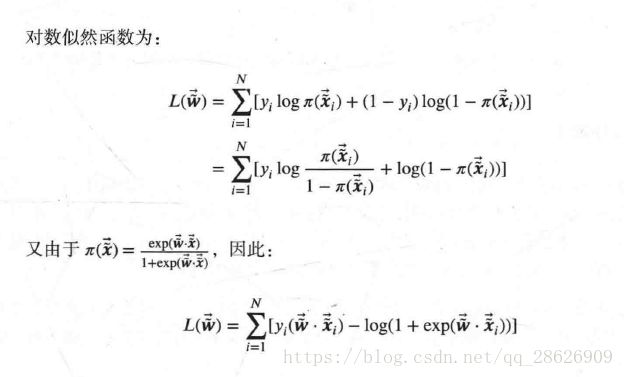机器学习之线性模型学习（python+所有代码）

一·普通线性回归

         线性模型（linear model)就是试图用一个线性组合来描述：

                                                 

       

        我们在其他很多的课程中肯定也接触到用层级结构或者高纬映射的线性模型去近似非线性模型（nonlinear model）。 由于线性模型的较好的可解释性（comprehensibility），例如

                                  

        线性模型非常简单，易于建模，应用广泛，它还有多种推广形式，包括岭回归、lasso回归，Elastic Net,逻辑回归，线性判断分析等

        对于已知的学习模型：我们根据已知训练集T来计算参数 和b

        我们的预测值为：

        我们采用平方损失函数，则在训练集T上，模型的损失函数为：

                                         

        我们目标的损失函数最小化，即：   

                                     

        这里我引用这本书中的一部分（本书的pdf最后会给出链接）：

                                          

        对于优化实际问题，可以采用最小二乘法解决：

                          

                         

                            

                                

                               

二·广义线性模型

                       

三·逻辑回归

               前面说的学习方法都是线性模型，而线性模型也可用于分类。我们考虑到是连续的，所以这个不能拟合离散变量。但是我们可以用它来拟合条件概率，因为概率的取值也是连续的。但是的取值是正无穷到负无穷，不符合0到1，所以我们利用到了单位阶跃函数：

                                                   

            但是单位阶跃函数不满足单调可导的性质。所以我们利用对数函数，让它成为一个可导的单位阶跃函数：

                                                         

            接下来由于大量的公式，我们还是引用上书中的内容：

            

                

            

三·代码实现

3.1所有函数输出均在print输出栏里，本次所有函数的数据集有两个

       第一个是：糖尿病病人数据集，函数为load_data(),白色的button，数据集有442个样本每个样本是个特征每个特征是浮点数，-0.2到0.2之间样本的目标都在25到346之间

       第二个是：鸢尾花分类，函数为load_data1(),黑色的button，鸢尾花一共有150个数据，每类50个，一共3类，数据集前50个样本类别为0，中间50个为1，后50个为2

 3.2代码中的函数如下图：

                                       

   3.3关键数值介绍：

   拿LinearRegression回归举例，

def test_LinearRegression(*data):  #线性回归模型
    X_train,X_test,y_train,y_test=data
    regr=linear_model.LinearRegression()
    regr.fit(X_train,y_train)
    print("--------------------------分割线-------------------------")
    print("LinearRegression回归")
    print('coefficient:%s,intercept%.2f'%(regr.coef_,regr.intercept_))  #coef_是权重向量，intercept是b值
    print("Residual sum of squares: %.2f"% np.mean((regr.predict(X_test)-y_test)**2))#模型预测返回，mean为均值
    print('score: %.2f' %regr.score(X_test,y_test))   #性能得分
    print("socre的值不会超过1，但可能为负数。值越大意味着性能越好")
    print("可以看出测试集中的预测结果的均方误差为3180.20，预测性能得分仅为0.36")
    print("--------------------------分割线-------------------------")

  Residual sum of squares： 是误差的平方的平均值
  score的计算公式如下图：

                                                   

LinearRegression的运行结果如下图：

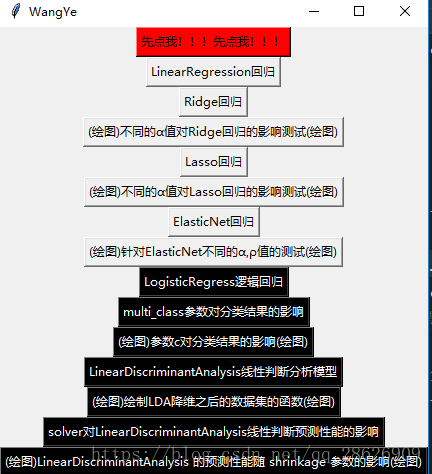
 程序执行的UI如下图：

点击相应的button会在出现相应的函数运行结果，结果均在控制台出现

                                   

3.4 所有代码：

#!D:/workplace/python
# -*- coding: utf-8 -*-
# @File  : Linear_model.py
# @Author: WangYe
# @Date  : 2018/6/20
# @Software: PyCharm
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets,linear_model,discriminant_analysis,cross_validation,model_selection
def load_data():
    #载入糖尿病病人数据集。数据集有442个样本
    #每个样本是个特征
    #每个特征是浮点数    -0.2到0.2之间
    #样本的目标都在25到346之间
    diabetes=datasets.load_diabetes()
    return cross_validation.train_test_split(diabetes.data,diabetes.target,
                                             test_size=0.25,random_state=0)
def test_LinearRegression(*data):  #线性回归模型
    X_train,X_test,y_train,y_test=data
    regr=linear_model.LinearRegression()
    regr.fit(X_train,y_train)
    print("--------------------------分割线-------------------------")
    print("LinearRegression回归")
    print('coefficient:%s,intercept：%.2f'%(regr.coef_,regr.intercept_))  #coef_是权重向量，intercept是b纸
    print("Residual sum of squares: %.2f"% np.mean((regr.predict(X_test)-y_test)**2))#模型预测返回，mean为均值
    print('score: %.2f' %regr.score(X_test,y_test))   #性能得分
    print("socre的值不会超过1，但可能为负数。值越大意味着性能越好")
    print("可以看出测试集中的预测结果的均方误差为3180.20，预测性能得分仅为0.36")
    print("--------------------------分割线-------------------------")
# X_train,X_test,y_train,y_test=load_data()
# test_LinearRegression(X_train,X_test,y_train,y_test)
#socre的值不会超过1，但可能为负数。值越大意味着性能越好
#第一步预测到此结束
def test_Ridge(*data):  #岭回归（使模型更加稳健）
    X_train, X_test, y_train, y_test = data
    regr = linear_model.Ridge()
    regr.fit(X_train, y_train)
    print("--------------------------分割线-------------------------")
    print("Ridge回归")
    print('coefficient:%s,intercept%.2f' % (regr.coef_, regr.intercept_))  # coef_是权重向量，intercept是b纸
    print("Residual sum of squares: %.2f" % np.mean((regr.predict(X_test) - y_test) ** 2))  # 模型预测返回，mean为均值
    print('score: %.2f' % regr.score(X_test, y_test))  # 性能得分
    print("socre的值不会超过1，但可能为负数。值越大意味着性能越好")
    print("可以看出测试集中的预测结果的均方误差为3192.33，预测性能得分仅为0.36")
    print("--------------------------分割线-------------------------")
# X_train, X_test, y_train, y_test = load_data()
# test_Ridge(X_train, X_test, y_train, y_test)
#针对不同的α值对于预测性能的影响测试
#第二步结束
def test_Ridge_alpha(*data):
    print("--------------------------分割线-------------------------")
    print("绘制不同的α值对于Ridge回归预测性能的影响测试")
    print("--------------------------分割线-------------------------")
    X_train, X_test, y_train, y_test = data
    alphas=[0.01,0.02,0.05,0.1,0.2,0.5,1,2,5,10,20,50,100,200,500,1000]
    scores=[]
    for i,alpha in enumerate(alphas):
        regr=linear_model.Ridge(alpha=alpha)
        regr.fit(X_train,y_train)
        scores.append(regr.score(X_test,y_test))
    #绘图
    fig=plt.figure()   #作用新建绘画窗口,独立显示绘画的图片
    ax=fig.add_subplot(1,1,1)
    # 这个比较重要,需要重点掌握,参数有r,c,n三个参数
    # 使用这个函数的重点是将多个图像画在同一个绘画窗口.
    # r  表示行数
    # c  表示列行
    # n  表示第几个
    ax.plot(alphas,scores)   #添加参数
    ax.set_xlabel(r"$\alpha$")  #转换α符号
    ax.set_ylabel(r"score")
    ax.set_xscale('log')  #x轴转换为对数
    ax.set_title("Ridge")
    plt.show()
# X_train, X_test, y_train, y_test = load_data()
# test_Ridge_alpha(X_train, X_test, y_train, y_test)
#第三步结束
#Lasso回归
#lasso回归可以将系数控制收缩到0，从而达到变量选择的效果，这是一种非常流行的选择方法
def test_Lasso(*data):  #岭回归（使模型更加稳健）
    X_train, X_test, y_train, y_test = data
    regr = linear_model.Lasso()
    regr.fit(X_train, y_train)
    print("--------------------------分割线-------------------------")
    print("Lasso回归")
    print('coefficient:%s,intercept%.2f' % (regr.coef_, regr.intercept_))  # coef_是权重向量，intercept是b纸
    print("Residual sum of squares: %.2f" % np.mean((regr.predict(X_test) - y_test) ** 2))  # 模型预测返回，mean为均值
    print('score: %.2f' % regr.score(X_test, y_test))  # 性能得分
    print("socre的值不会超过1，但可能为负数。值越大意味着性能越好")
    print("可以看出测试集中的预测结果的均方误差为3583.42，预测性能得分仅为0.28")
    print("--------------------------分割线-------------------------")
# X_train, X_test, y_train, y_test = load_data()
# test_Lasso(X_train, X_test, y_train, y_test)
#岭回归结束结束
#针对岭回归，我们也采用不同的α值进行测试
def test_Lasso_alpha(*data):
    print("--------------------------分割线-------------------------")
    print("针对岭回归，我们也采用不同的α值进行绘图测试")
    print("--------------------------分割线-------------------------")
    X_train, X_test, y_train, y_test = data
    alphas=[0.01,0.02,0.05,0.1,0.2,0.5,1,2,5,10,20,50,100,200,500,1000]
    scores=[]
    for i,alpha in enumerate(alphas):
        regr=linear_model.Lasso(alpha=alpha)
        regr.fit(X_train,y_train)
        scores.append(regr.score(X_test,y_test))
    #绘图
    fig=plt.figure()   #作用新建绘画窗口,独立显示绘画的图片
    ax=fig.add_subplot(1,1,1)
    ax.plot(alphas,scores)   #添加参数
    ax.set_xlabel(r"$\alpha$")  #转换α符号
    ax.set_ylabel(r"score")
    ax.set_xscale('log')  #x轴转换为对数
    ax.set_title("Lasso")
    plt.show()
# X_train, X_test, y_train, y_test = load_data()
# test_Lasso_alpha(X_train, X_test, y_train, y_test)
#岭回归α值测试结束
#ElasticNet回归测试
def test_ElasticNet(*data):  #岭回归（使模型更加稳健）
    X_train, X_test, y_train, y_test = data
    regr = linear_model.ElasticNet()
    regr.fit(X_train, y_train)
    print("--------------------------分割线-------------------------")
    print("ElasticNet回归")
    print('coefficient:%s,intercept%.2f' % (regr.coef_, regr.intercept_))  # coef_是权重向量，intercept是b纸
    print("Residual sum of squares: %.2f" % np.mean((regr.predict(X_test) - y_test) ** 2))  # 模型预测返回，mean为均值
    print('score: %.2f' % regr.score(X_test, y_test))  # 性能得分
    print("socre的值不会超过1，但可能为负数。值越大意味着性能越好")
    print("可以看出测试集中的预测结果的均方误差为4922.36，预测性能得分仅为0.01")
    print("--------------------------分割线-------------------------")
# X_train, X_test, y_train, y_test = load_data()
# test_ElasticNet(X_train, X_test, y_train, y_test)
#ElasticNet预测回归结束
#针对ElasticNet不同的α,ρ值的测试
def test_ElasticNet_alpha_rho(*data):
    print("--------------------------分割线-------------------------")
    print("针对ElasticNet不同的α,ρ值绘图测试")
    print("--------------------------分割线-------------------------")
    X_train, X_test, y_train, y_test = data
    alphas=np.logspace(-2,2)    #α值区间
    rhos=np.linspace(0.01,1)    #ρ值区间
    scores=[]
    for alpha in alphas:
        for rho in rhos:
            regr=linear_model.ElasticNet(alpha=alpha,l1_ratio=rho)   #针对α和ρ的值来判断最终值
            regr.fit(X_train,y_train)
            scores.append(regr.score(X_test,y_test))
    #绘图
    alphas,rhos=np.meshgrid(alphas,rhos)
    scores=np.array(scores).reshape(alphas.shape)
    from mpl_toolkits.mplot3d import Axes3D
    from matplotlib import cm
    fig=plt.figure()   #作用新建绘画窗口,独立显示绘画的图片
    ax=Axes3D(fig)
    surf=ax.plot_surface(alphas,rhos,scores,rstride=1,cstride=1,
                         cmap=cm.jet,linewidth=0,antialiased=False)
    fig.colorbar(surf,shrink=0.5,aspect=5)
    ax.set_xlabel(r"$\alpha$")  #转换α符号
    ax.set_ylabel(r"$\rho$")  # 转换ρ符号
    ax.set_zlabel("score")
    ax.set_title("ElasticNet")
    plt.show()
# X_train, X_test, y_train, y_test = load_data()
# test_ElasticNet_alpha_rho(X_train, X_test, y_train, y_test)
#NlasticNet针对α和ρ的变化的三维坐标完成
#逻辑回归，首先先将载入函数进行修改
def load_data1():    #数据集更换，换为花的数据集
    iris=datasets.load_iris()
    X_train=iris.data
    y_train=iris.target
    return cross_validation.train_test_split(X_train,y_train,test_size=0.25,random_state=0,stratify=y_train)
#数据集前50个样本类别为0，中间50个位1，后50个位2
def test_LogisticRegress(*data):
    X_train,X_test,y_train,y_test=data
    regr=linear_model.LogisticRegression()
    regr.fit(X_train,y_train)
    print("--------------------------分割线-------------------------")
    print("LogisticRegress逻辑回归")
    print('coefficient:%s,intercept%s' % (regr.coef_, regr.intercept_))  # coef_是权重向量，intercept是b纸
   # print("Residual sum of squares: %.2f" % np.mean((regr.predict(X_test) - y_test) ** 2))  # 模型预测返回，mean为均值
    print('score: %.2f' % regr.score(X_test, y_test))  # 性能得分
    print("可以看出测试集中的预测结果性能得分为0.97（即准确率97%）")
    print("--------------------------分割线-------------------------")
# X_train, X_test, y_train, y_test = load_data1()
# test_LogisticRegress(X_train, X_test, y_train, y_test)
#这个记过预测是0.97，即准确率为97%
#下面考察multi_class参数对分类结果的影响。默认采用的是one-vs-rest策略
#但是逻辑回归模型原生就支持多类分类
def test_LogisticRegression_multinomial(*data):
    X_train, X_test, y_train, y_test = data
    regr = linear_model.LogisticRegression(multi_class='multinomial',solver='lbfgs')
    regr.fit(X_train, y_train)
    print("--------------------------分割线-------------------------")
    print("LogisticRegress逻辑回归multi_class参数对分类结果的影响")
    print("考察multi_class参数对分类结果的影响。默认采用的是one-vs-rest策略")
    print('coefficient:%s,intercept%s' % (regr.coef_, regr.intercept_))  # coef_是权重向量，intercept是b纸
    # print("Residual sum of squares: %.2f" % np.mean((regr.predict(X_test) - y_test) ** 2))  # 模型预测返回，mean为均值
    print('score: %.2f' % regr.score(X_test, y_test))  # 性能得分
    print("可以看出测试集中的预测结果性能得分为1（即准确率100%）,说明LogisticRegression分类器完全预测正确")
    print("--------------------------分割线-------------------------")
# X_train, X_test, y_train, y_test = load_data1()
# test_LogisticRegression_multinomial(X_train, X_test, y_train, y_test)
#本次性能的结果预测为1，可以看到这个问题中，多分类策略进一步提高了预测的准确率，说明对于测试集中的数据LogisticRegression分类器是完全正确的
#最后我们考察参数c对分类器模型的预测性能的影响。c是正则化项系数的倒数，它越小则正则化项的权重越大，测试函数如下
def test_LogisticRegression_C(*data):
    print("--------------------------分割线-------------------------")
    print("考察参数c对分类器模型的预测性能的影响。c是正则化项系数的倒数，它越小则正则化项的权重越大。绘图")
    print("--------------------------分割线-------------------------")
    X_train, X_test, y_train, y_test = data
    Cs=np.logspace(-2,4,num=100)
    scores=[]
    for C in Cs:
        regr=linear_model.LogisticRegression(C=C)
        regr.fit(X_train,y_train)
        scores.append(regr.score(X_test,y_test))
#绘图
    fig=plt.figure()   #作用新建绘画窗口,独立显示绘画的图片
    ax=fig.add_subplot(1,1,1)
    ax.plot(Cs,scores)   #添加参数
    ax.set_xlabel(r"C")  #转换α符号
    ax.set_ylabel(r"score")
    ax.set_xscale('log')  #x轴转换为对数
    ax.set_title("LogisticRegression")
    plt.show()
# X_train, X_test, y_train, y_test = load_data1()
# test_LogisticRegression_C(X_train, X_test, y_train, y_test)
#绘图结束
#在scikit-learn中，LinearDiscriminantAnalysis实现了线性判断分析模型
def test_LinearDiscriminantAnalysis(*data):
    X_train, X_test, y_train, y_test = data
    lda=discriminant_analysis.LinearDiscriminantAnalysis()
    lda.fit(X_train,y_train)
    print("--------------------------分割线-------------------------")
    print("LinearDiscriminantAnalysis线性判断分析模型")
    print('coefficient:%s,intercept%s' % (lda.coef_, lda.intercept_))  # coef_是权重向量，intercept是b纸
    # print("Residual sum of squares: %.2f" % np.mean((regr.predict(X_test) - y_test) ** 2))  # 模型预测返回，mean为均值
    print('score: %.2f' % lda.score(X_test, y_test))  # 性能得分
    print("可以看出测试集中的预测结果性能得分为1（即准确率100%）,说明LinearDiscriminantAnalysis对于测试集的预测完全正确")
    print("--------------------------分割线-------------------------")
# X_train, X_test, y_train, y_test = load_data1()
# test_LinearDiscriminantAnalysis(X_train, X_test, y_train, y_test)
#本次对测试集的预测准确率为1.0，说明LinearDiscriminantAnalysis对于测试集的预测完全正确
#接下来我们检查一下原始数据集在经过线性判断LDA之后的数据集的情况。给出绘制LDA降维之后的数据集的函数
def plot_LDA(converted_X,y):
    print("--------------------------分割线-------------------------")
    print("检查一下原始数据集在经过线性判断LDA之后的数据集的情况。给出绘制LDA降维之后的数据集的函数")
    print("--------------------------分割线-------------------------")
    from mpl_toolkits.mplot3d import Axes3D
    fig = plt.figure()
    ax = Axes3D(fig)
    colors = 'rgb'
    markers = 'o*s'
    for target, color, marker in zip([0, 1, 2], colors, markers):
        pos = (y == target).ravel()
        X = converted_X[pos, :]
        ax.scatter(X[:, 0], X[:, 1], X[:, 2], color=color, marker=marker,label="Label %d" % target)
    ax.legend(loc="best")
    fig.suptitle("Iris After LDA")
    plt.show()
# X_train, X_test, y_train, y_test = load_data1()
# X=np.vstack((X_train,X_test))
# Y=np.vstack((y_train.reshape(y_train.size,1),y_test.reshape(y_test.size,1)))
# lda=discriminant_analysis.LinearDiscriminantAnalysis()
# lda.fit(X,Y)
# converted_X=np.dot(X,np.transpose(lda.coef_))+lda.intercept_
# plot_LDA(converted_X,Y)

#接下来考察不同的solver对预测性能的影响
def test_LinearDiscriminantAnalysis_solver(*data):
    X_train,X_test,y_train,y_test=data
    solvers=['svd','lsqr','eigen']
    for solver in solvers:
        if(solver=='svd'):
            lda = discriminant_analysis.LinearDiscriminantAnalysis(solver=solver)
        else:
            lda = discriminant_analysis.LinearDiscriminantAnalysis(solver=solver,
			shrinkage=None)
        lda.fit(X_train, y_train)
    print("--------------------------分割线-------------------------")
    print("考察不同的solver对预测性能的影响")
    print('Score at solver=%s: %.2f' %(solver, lda.score(X_test, y_test)))
    print('测试结果如下：')
    print("score at solver=svd: 1.00")
    print("score at solver=lsqr: 1.00")
    print("score at solver=eigen: 1.00")
    print("可以看出，三者没有差别")
    print("--------------------------分割线-------------------------")
# X_train, X_test, y_train, y_test = load_data1()
# test_LinearDiscriminantAnalysis(X_train, X_test, y_train, y_test)
def test_LinearDiscriminantAnalysis_shrinkage(*data):
    print("--------------------------分割线-------------------------")
    print("solver=lsqr中引入了抖动，引入抖动相当于引入了正则化项")
    print("LinearDiscriminantAnalysis 的预测性能随 shrinkage 参数的影响。绘图")
    print("--------------------------分割线-------------------------")

    # 测试  LinearDiscriminantAnalysis 的预测性能随 shrinkage 参数的影响
    # :param data: 可变参数。它是一个元组，这里要求其元素依次为：训练样本集、测试样本集、训练样本的标记、测试样本的标记
    # :return:  None

    X_train,X_test,y_train,y_test=data
    shrinkages=np.linspace(0.0,1.0,num=20)
    scores=[]
    for shrinkage in shrinkages:
        lda = discriminant_analysis.LinearDiscriminantAnalysis(solver='lsqr',
			shrinkage=shrinkage)
        lda.fit(X_train, y_train)
        scores.append(lda.score(X_test, y_test))
    ## 绘图
    fig=plt.figure()
    ax=fig.add_subplot(1,1,1)
    ax.plot(shrinkages,scores)
    ax.set_xlabel(r"shrinkage")
    ax.set_ylabel(r"score")
    ax.set_ylim(0,1.05)
    ax.set_title("LinearDiscriminantAnalysis")
    plt.show()
# X_train, X_test, y_train, y_test = load_data1()
# test_LinearDiscriminantAnalysis_shrinkage(X_train, X_test, y_train, y_test)

from tkinter import *
def run0():
    print("--------------------------分割线-------------------------")
    print("所有函数输出均在print输出栏里")
    print("本次所有函数的数据集有两个")
    print("第一个是：糖尿病病人数据集，函数为load_data(),白色的button")
    print('数据集有442个样本每个样本是个特征每个特征是浮点数')
    print('-0.2到0.2之间样本的目标都在25到346之间')
    print('第二个是：鸢尾花分类，函数为load_data1(),黑色的button')
    print('鸢尾花一共有150个数据，每类50个，一共3类')
    print('数据集前50个样本类别为0，中间50个位1，后50个位2')
    print("--------------------------分割线-------------------------")
def run1():
    X_train, X_test, y_train, y_test = load_data()
    test_LinearRegression(X_train, X_test, y_train, y_test)
def run2():
    X_train, X_test, y_train, y_test = load_data()
    test_Ridge(X_train, X_test, y_train, y_test)
def run3():
    X_train, X_test, y_train, y_test = load_data()
    test_Ridge_alpha(X_train, X_test, y_train, y_test)
def run4():
    X_train, X_test, y_train, y_test = load_data()
    test_Lasso(X_train, X_test, y_train, y_test)
def run5():
    X_train, X_test, y_train, y_test = load_data()
    test_Lasso_alpha(X_train, X_test, y_train, y_test)
def run6():
    X_train, X_test, y_train, y_test = load_data()
    test_ElasticNet(X_train, X_test, y_train, y_test)
def run7():
    X_train, X_test, y_train, y_test = load_data()
    test_ElasticNet_alpha_rho(X_train, X_test, y_train, y_test)
def run8():
    X_train, X_test, y_train, y_test = load_data1()
    test_LogisticRegress(X_train, X_test, y_train, y_test)
def run9():
    X_train, X_test, y_train, y_test = load_data1()
    test_LogisticRegression_multinomial(X_train, X_test, y_train, y_test)
def run10():
    X_train, X_test, y_train, y_test = load_data1()
    test_LogisticRegression_C(X_train, X_test, y_train, y_test)
def run11():
    X_train, X_test, y_train, y_test = load_data1()
    test_LinearDiscriminantAnalysis(X_train, X_test, y_train, y_test)
def run12():
    X_train, X_test, y_train, y_test = load_data1()
    X=np.vstack((X_train,X_test))
    Y=np.vstack((y_train.reshape(y_train.size,1),y_test.reshape(y_test.size,1)))
    lda=discriminant_analysis.LinearDiscriminantAnalysis()
    lda.fit(X,Y)
    converted_X=np.dot(X,np.transpose(lda.coef_))+lda.intercept_
    plot_LDA(converted_X,Y)
def run13():
    X_train, X_test, y_train, y_test = load_data1()
    test_LinearDiscriminantAnalysis_solver(X_train, X_test, y_train, y_test)
def run14():
    X_train, X_test, y_train, y_test = load_data1()
    test_LinearDiscriminantAnalysis_shrinkage(X_train, X_test, y_train, y_test)
if __name__=='__main__':
    root = Tk()
    #root.geometry('500x500')
    root.title('WangYe')
    btn0 = Button(root, text='先点我！！！先点我！！！',bg='red', command=run0).pack()
    btn1 = Button(root, text='LinearRegression回归', command=run1).pack()
    btn2 = Button(root, text='Ridge回归', command=run2).pack()
    btn3 = Button(root, text='(绘图)不同的α值对Ridge回归的影响测试(绘图)', command=run3).pack()
    btn4 = Button(root, text='Lasso回归', command=run4).pack()
    btn5 = Button(root, text='(绘图)不同的α值对Lasso回归的影响测试(绘图)', command=run5).pack()
    btn6 = Button(root, text='ElasticNet回归', command=run6).pack()
    btn7 = Button(root, text='(绘图)针对ElasticNet不同的α,ρ值的测试(绘图)', command=run7).pack()
    btn8 = Button(root, text='LogisticRegress逻辑回归',fg='white',bg='black',command=run8).pack()
    btn9 = Button(root, text='multi_class参数对分类结果的影响',fg='white',bg='black', command=run9).pack()
    btn10= Button(root, text='(绘图)参数c对分类结果的影响(绘图)',fg='white',bg='black', command=run10).pack()
    btn11= Button(root, text='LinearDiscriminantAnalysis线性判断分析模型',fg='white',bg='black', command=run11).pack()
    btn12= Button(root, text='(绘图)绘制LDA降维之后的数据集的函数(绘图)',fg='white',bg='black', command=run12).pack()
    btn13= Button(root, text='solver对LinearDiscriminantAnalysis线性判断预测性能的影响',fg='white',bg='black', command=run13).pack()
    btn14= Button(root, text='(绘图)LinearDiscriminantAnalysis 的预测性能随 shrinkage 参数的影响(绘图)', fg='white',bg='black',command=run14).pack()
    root.mainloop()

 

 这个代码我亲测可以，跑得起来~如果有什么问题可以留言

参考文献：https://blog.csdn.net/zmdsjtu/article/details/52891654

               《python大战机器学习》 华校专，王正林著  电子工业出版社2017年

《python大战机器学习》 书籍免费链接：

链接：https://pan.baidu.com/s/1xHP7zVhL2u0hhebF665YwA 密码：0gt2