TensorFlow学习笔记：构建多分类任务模型(未完)

任务描述

识别手势：

如上图所示，对于多分类任务，输出一个独热码矩阵：即仅有一个元素为1，其他元素均为0的列向量。

数据

训练集：0-5的手势图片各180张，像素为64*64。
测试集：0-5的手势图片各20张，像素为64*64。

载入数据

X_train_orig, Y_train_orig, X_test_orig, Y_test_orig, classes = load_dataset()

数据处理

# Flatten the training and test images
X_train_flatten = X_train_orig.reshape(X_train_orig.shape[0], -1).T
X_test_flatten = X_test_orig.reshape(X_test_orig.shape[0], -1).T

# Normalize image vectors
X_train = X_train_flatten/255.
X_test = X_test_flatten/255.

# Convert training and test labels to one hot matrices
Y_train = convert_to_one_hot(Y_train_orig, 6)
Y_test = convert_to_one_hot(Y_test_orig, 6)

构建模型

构建一个三层多分类模型，其中最后一层使用SOFTMAX激活函数：
LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SOFTMAX

创建placeholder

placeholder常用于等待样本X与标记Y输入：

def create_placeholders(n_x, n_y):
    """
    Creates the placeholders for the tensorflow session.

    Returns:
    X -- placeholder for the data input, of shape [n_x, None] and dtype "float"
    Y -- placeholder for the input labels, of shape [n_y, None] and dtype "float"
    """

    X = tf.placeholder(tf.float32,name="X",shape=[n_x,None])
    Y = tf.placeholder(tf.float32,name="Y",shape=[n_y,None])

    return X, Y

初始化参数

对于权重参数 W[i] 使用Xavier初始化(详见He初始化方法，两者类似)，对于偏差参数 b[i] 使用零初始化：

def initialize_parameters():
    tf.set_random_seed(1)

    W1 = tf.get_variable("W1",[25,12288],initializer=tf.contrib.layers.xavier_initializer(seed = 1))
    b1 = tf.get_variable("b1", [25,1], initializer = tf.zeros_initializer())
    W2 = tf.get_variable("W2",[12,25],initializer=tf.contrib.layers.xavier_initializer(seed = 1))
    b2 = tf.get_variable("b2", [12,1], initializer = tf.zeros_initializer())
    W3 = tf.get_variable("W3",[6,12],initializer=tf.contrib.layers.xavier_initializer(seed = 1))
    b3 = tf.get_variable("b3", [6,1], initializer = tf.zeros_initializer())

    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2,
                  "W3": W3,
                  "b3": b3}
    return parameters

前向传播

def forward_propagation(X, parameters):
    """
    Implements the forward propagation for the model: LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SOFTMAX
    """

    # Retrieve the parameters from the dictionary "parameters" 
    W1 = parameters['W1']
    b1 = parameters['b1']
    W2 = parameters['W2']
    b2 = parameters['b2']
    W3 = parameters['W3']
    b3 = parameters['b3']

    Z1 = tf.add(tf.matmul(W1,X),b1)
    A1 = tf.nn.relu(Z1)                     
    Z2 = tf.add(tf.matmul(W2,A1),b2)
    A2 = tf.nn.relu(Z2)          
    Z3 = tf.add(tf.matmul(W3,A2),b3)

    return Z3

tf.matmul()为矩阵乘法。注意到这里并没有计算A3，因为在tensorflow中最后一层的线性输出会被直接用于计算损失。

计算损失

tensorflow提供了计算交叉熵损失的函数tf.nn.softmax_cross_entropy_with_logits(logits = ..., labels = ...)，不过需要注意它接受的参数矩阵形状必须为(样本个数,样本类目数)。

def compute_cost(Z3, Y):
    # to fit the tensorflow requirement for tf.nn.softmax_cross_entropy_with_logits(...,...)
    logits = tf.transpose(Z3)
    labels = tf.transpose(Y)

    cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=logits,labels=labels))

    return cost

反向传播与参数更新

使用框架时，通常不需要考虑反向传播的具体过程，因为所有的反向传播与参数更新在框架中能用一行代码来实现。

在实现损失函数之后，创建一个“优化器”对象，在一个会话中同时运行“优化器”与损失函数，它会根据给定的损失来按照制定方法与学习率进行优化。

整合模型

def model(X_train, Y_train, X_test, Y_test, learning_rate = 0.0001,
          num_epochs = 1500, minibatch_size = 32, print_cost = True):
    """
    Implements a three-layer tensorflow neural network: LINEAR->RELU->LINEAR->RELU->LINEAR->SOFTMAX.

    Arguments:
    num_epochs -- number of epochs of the optimization loop
    print_cost -- True to print the cost every 100 epochs
    """

    ops.reset_default_graph()                         # to be able to rerun the model without overwriting tf variables
    tf.set_random_seed(1)
    seed = 3
    (n_x, m) = X_train.shape         
    n_y = Y_train.shape[0]                            # n_y : output size
    costs = []                                        # To keep track of the cost

    X, Y = create_placeholders(n_x,n_y)

    parameters = initialize_parameters()

    Z3 = forward_propagation(X,parameters)

    cost = compute_cost(Z3,Y)

    # Backpropagation: Define the tensorflow optimizer. Use an AdamOptimizer.
    optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate).minimize(cost)

    init = tf.global_variables_initializer()

    # Start the session to compute the tensorflow graph
    with tf.Session() as sess:
        sess.run(init)

        for epoch in range(num_epochs):
            epoch_cost = 0.                       #每对整个样本进行一次训练称为一个epoch
            num_minibatches = int(m / minibatch_size) # number of minibatches
            seed = seed + 1
            minibatches = random_mini_batches(X_train, Y_train, minibatch_size, seed)

            for minibatch in minibatches:
                (minibatch_X, minibatch_Y) = minibatch

                # Run the session to execute the "optimizer" and the "cost"
                _ , minibatch_cost = sess.run([optimizer,cost],feed_dict={X:minibatch_X,Y:minibatch_Y})

                epoch_cost += minibatch_cost / num_minibatches    #取均值

            # Print the cost every epoch
            if print_cost == True and epoch % 100 == 0:
                print ("Cost after epoch %i: %f" % (epoch, epoch_cost))
            if print_cost == True and epoch % 5 == 0:
                costs.append(epoch_cost)

        # plot the cost
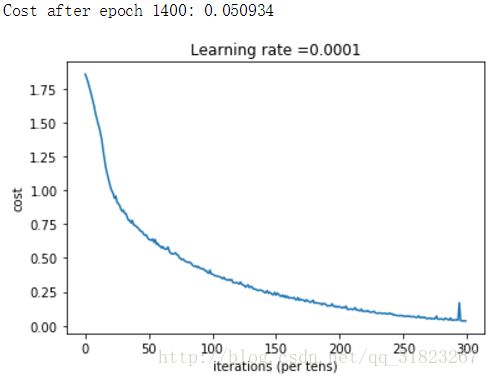
        plt.plot(np.squeeze(costs))
        plt.ylabel('cost')
        plt.xlabel('iterations (per tens)')
        plt.title("Learning rate =" + str(learning_rate))
        plt.show()

        parameters = sess.run(parameters)
        print ("Parameters have been trained!")

        correct_prediction = tf.equal(tf.argmax(Z3), tf.argmax(Y))

        accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))

        print ("Train Accuracy:", accuracy.eval({X: X_train, Y: Y_train}))
        print ("Test Accuracy:", accuracy.eval({X: X_test, Y: Y_test}))

        return parameters

训练模型

parameters = model(X_train, Y_train, X_test, Y_test)

模型表现

损失与代价曲线

准确度

有理由怀疑此模型产生了过拟合现象。