【机器学习】次梯度(subgradient)方法
次梯度方法(subgradient method)是传统的梯度下降方法的拓展,用来处理不可导的凸函数。它的优势是比传统方法处理问题范围大,劣势是算法收敛速度慢。但是,由于它对不可导函数有很好的处理方法,所以学习它还是很有必要的。
次导数
设f:I→R是一个实变量凸函数,定义在实数轴上的开区间内。这种函数不一定是处处可导的,例如最经典的例子就是![]() ,在
,在![]() 处不可导。但是,从下图的可以看出,对于定义域内的任何
处不可导。但是,从下图的可以看出,对于定义域内的任何![]() ,我们总可以作出一条直线,它通过点
,我们总可以作出一条直线,它通过点![]() ,并且要么接触f的图像,要么在它的下方。这条直线的斜率称为函数的次导数。
,并且要么接触f的图像,要么在它的下方。这条直线的斜率称为函数的次导数。
次导数与次微分(subdifferential)计算方式
凸函数f:I→R在点x0的次导数,是实数c使得:
![]()
对该定义略作解释:
按照上面次导数对定义方式,次导数c应满足条件:
对于函数
而言,只有在
处不可导,即我们考虑在
处的次导数:
很容易就可以得出:
接下来给出正宗的计算定义:
对于所有I内的x。我们可以证明,在点x0的次导数的集合是一个非空闭区间[a, b],其中a和b是单侧极限
它们一定存在,且满足a ≤ b。
所有次导数的集合![]() 称为函数f在
称为函数f在![]() 的次微分。
的次微分。
例如:考虑凸函数![]() 。在原点的次微分是区间[−1, 1]。
。在原点的次微分是区间[−1, 1]。![]() 时,次微分是单元素集合{-1},而
时,次微分是单元素集合{-1},而![]() ,则是单元素集合{1}。
,则是单元素集合{1}。
次导数与次微分的一些性质
- 凸函数f:I→R在
 可导,当且仅当次微分只由一个点组成,这个点就是函数在
可导,当且仅当次微分只由一个点组成,这个点就是函数在 的导数。
的导数。 - 点
 是凸函数f的最小值,当且仅当次微分中包含零,也就是说,在上面的图中,我们可以作一条水平的“次切线”。这个性质是“可导函数在极小值的导数是零”的事实的推广。
是凸函数f的最小值,当且仅当次微分中包含零,也就是说,在上面的图中,我们可以作一条水平的“次切线”。这个性质是“可导函数在极小值的导数是零”的事实的推广。
次梯度(subgradient)
到这里,我们总算是搞清楚次导数和次微分是什么东西了。
将次导数和次微分的概念推广到多元函数,就可以得到次梯度了。如果f:U→ R是一个实变量凸函数,定义在欧几里得空间![]() 内的凸集,则该空间内的向量v称为函数在点
内的凸集,则该空间内的向量v称为函数在点![]() 的次梯度,如果对于所有U内的x,都有:
的次梯度,如果对于所有U内的x,都有:
![]()
所有次梯度的集合称为次微分,记为![]()
![]() 。次微分总是非空的凸紧集。
。次微分总是非空的凸紧集。
此记法与前面的次导数记法极为相似。我们用更为常见的记法来定义次梯度:
次梯度(Subgradient)与梯度的概念类似,凸函数的First-order characterization(一阶特征描述)是指如果函数f可微,那么当且仅当为凸集,且对于
,使得
,则函数
为凸函数。这里所说的次梯度是指在函数
上的点
满足以下条件的
:
其中,函数
不一定要是凸函数,非凸函数也可以,即对于凸函数或者非凸函数而言,满足上述条件的
均为函数在该点的次梯度。但是,凸函数总是存在次梯度(可以利用epigraph和支撑平面理论证明),而非凸函数则不一定存在次梯度,即使
可微。这里主要包含两层意思:1.用次梯度对原函数做出的泰勒一阶展开估计总是比真实值要小;2.次梯度可能不唯一。
很明显,凸函数的次梯度一定存在,如果函数![]() 在点
在点![]() 处可微,那么
处可微,那么![]() ,为函数在该点的梯度,且唯一;如果不可微,则次梯度不一定唯一。但是对于非凸函数,次梯度则不一定存在,也不一定唯一。例如,凸函数
,为函数在该点的梯度,且唯一;如果不可微,则次梯度不一定唯一。但是对于非凸函数,次梯度则不一定存在,也不一定唯一。例如,凸函数![]() 范数为凸函数,但不满足处处可微的条件,因此,函数的次梯度不一定唯一,如下图:
范数为凸函数,但不满足处处可微的条件,因此,函数的次梯度不一定唯一,如下图:
左一图为![]() ,函数在
,函数在![]() 时,次梯度唯一,且
时,次梯度唯一,且![]() ;当
;当![]() 时,次梯度为
时,次梯度为![]() 中的任意一个元素;
中的任意一个元素;
左二图为![]() ,函数在
,函数在![]() 时,次梯度唯一,且
时,次梯度唯一,且![]() ;当
;当![]() 时,次梯度为
时,次梯度为![]() 中的任意一个元素;
中的任意一个元素;
同样,绝对值函数![]() 和最大值函数
和最大值函数![]() 在不可微点处次梯度也不一定唯一,如下图:
在不可微点处次梯度也不一定唯一,如下图:
对于最大值函数而言,其在满足![]() 的点处,次梯度为任意一条直线在向量
的点处,次梯度为任意一条直线在向量![]() 和
和![]() 之间。
之间。
同理,我们还可以给出在高维情形下次微分(subdifferential)的定义,即:
![]()
-
次微分是闭合且为凸集;
-
如果函数
 在点
在点 处可微,那么次微分等于梯度;
处可微,那么次微分等于梯度; -
凸函数的次微分不为空,但非凸函数则不一定。
次梯度的性质
-
Scalingf(数乘不变性):
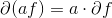 ;
; -
Addition(加法不变性):
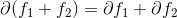 ;
; -
Affine composition(仿射特性):如果
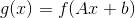 ,那么
,那么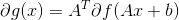 ;
; -
Finite pointwise maximum(有限最大值):如果
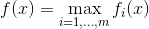 ,那么
,那么 ,意味着函数
,意味着函数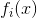 的次微分等于所有能取得最大值的函数
的次微分等于所有能取得最大值的函数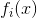 在点
在点 处的微分,具体实例可参考之前提到的最大值函数部分。
处的微分,具体实例可参考之前提到的最大值函数部分。
为什么要计算次梯度?
在开头已经粗略的阐述了次梯度方法的使用情景,在这里在详细的复述一遍。
对于光滑的凸函数而言,我们可以直接采用梯度下降算法求解函数的极值,但是当函数不处处光滑、处处可微的时候,梯度下降就不适合应用了。因此,我们需要计算函数的次梯度。对于次梯度而言,其没有要求函数是否光滑,是否是凸函数,限定条件很少,所以适用范围更广。
次梯度具有以下优化条件(subgradient optimality condition):对于任意函数
(无论是凸还是非凸),函数在点
处取得最值等价于:
即,当且仅当0属于函数
在点
处次梯度集合的元素时,
为最优解。
这与之前所描述的次导数的性质相符合。
证明:
证明很简单,当次梯度
时,对于所有
,存在
,所以,
为最优解,即证。
次梯度算法
介绍完前面的基础知识,终于要开始介绍算法了~
经典梯度下降算法实际上是利用负梯度总是指向最小值点这一性质,然后每次迭代 ![]() ,
, ![]() 是一个很小的控制步进长度的数,可以是常量也可以是变量,迭代过程一直进行直到收敛。
是一个很小的控制步进长度的数,可以是常量也可以是变量,迭代过程一直进行直到收敛。
次梯度算法(Subgradient method)与梯度下降算法类似,仅仅用次梯度代替梯度,即:
![]()
其中,![]() ,为
,为![]() 在点
在点![]() 处的次梯度。
处的次梯度。
与梯度下降算法不同的地方在于,次梯度算法并不是下降算法,每次对于参数的更新并不能保证代价函数是呈单调递减的趋势,因此,一般情况下我们选择:
另一点与梯度下降算法不同的是:次梯度算法没有明确的步长选择方法,类似Exact line search和Backtracking line search的方法,只有步长选择准则,具体如下:
Fixed step sizes: ;
;Diminishing step sizes: 选择满足以下条件的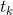 :
:
Diminishing step sizes方法主要是保证步长逐渐变小,同时,变化幅度还不会特别快。这里需要注意的是,次梯度算法并不像梯度下降一样,可以在每一次迭代过程中自适应的计算此次步长(adaptively computed),而是事先设定好的(pre-specified)。
但是,很多人会提出这样一个问题,如果你不能保证次梯度是单调的,如何保证最后可以收敛?
定理:如果![]() 为凸函数,且满足Lipschitz continuous with G,如果固定步长为
为凸函数,且满足Lipschitz continuous with G,如果固定步长为![]() ,那么次梯度算法满足:
,那么次梯度算法满足:
lipschitz条件:
对于在实数集的子集的函数
,若存在常数,使得
,则称
符合利普希茨条件,对于
最小的常数
称为
的利普希茨常数。若
,
称为收缩映射。
在高维情形下:
证明:
对于![]() ,
,![]() ,其中
,其中![]() 。因此,我们可以展开下式为:
。因此,我们可以展开下式为:
因为,![]() ,且由凸函数一阶性质可得
,且由凸函数一阶性质可得![]() ,上式不等式可以写为:
,上式不等式可以写为:
![]()
对于任意![]() ,求和上式可以获得:
,求和上式可以获得:
因为,![]() ,所以:
,所以:
如果令![]() 为迭代
为迭代![]() 次内的最优解,那么
次内的最优解,那么![]() ,其中,
,其中,![]() ,因此:
,因此:
同时,因为函数满足Lipschitz continuous with G,所以,![]() ,即函数的次梯度
,即函数的次梯度![]() 。
。
综上所述,我们可以证明下式成立:
其中![]() 为初值
为初值![]() 与最优点
与最优点![]() 之间的二范数距离。
之间的二范数距离。
当![]() ,既证上述定理成立。
,既证上述定理成立。
此时,如果我们想要获得![]() -最优解,则令
-最优解,则令![]() ,令等式的每一部分等于
,令等式的每一部分等于![]() ,则
,则![]() 。
。
因此,次梯度的收敛速度为![]() ,跟梯度下降算法收敛速度
,跟梯度下降算法收敛速度![]() 相比,要慢许多。
相比,要慢许多。
下面是次梯度法的一般方法:
 选择有限的正的迭代步长
选择有限的正的迭代步长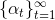
- 计算一个次梯度
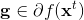
- 更新
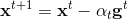
- 若是算法没有收敛,则
 返回第二步继续计算
返回第二步继续计算
次梯度方法性质:
- 简单通用性:就是说第二步中,
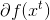 任何一个次梯度都是可以的。
任何一个次梯度都是可以的。 - 收敛性:只要选择的步长合适,总会收敛的。
- 收敛慢:需要大量的迭代才能收敛。
- 非单调收敛:
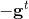 不一定是下降方向,在这种情况下,不能使用线性搜索选择合适的
不一定是下降方向,在这种情况下,不能使用线性搜索选择合适的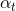 。
。 - 没有很好的停止准则。
对于不同步长的序列的收敛结果
1).步长和不可消时(Non-summable diminishing step size):
2).Constant step size:
![]() ,收敛到次优解:
,收敛到次优解:![]()
3).Constant step length:
次梯度算法实例
A. Regularized Logistic Regression
对于逻辑回归的代价函数可记为:
明显,上式是光滑且凸的,而regularized problem则是指优化目标函数为:
![]()
如果![]() ,则成为岭回归(ridge problem),如果
,则成为岭回归(ridge problem),如果![]() 则称为Lasso回归。对于岭回归,我们仍然可以采用梯度下降算法求解目标函数,因为函数处处可导光滑,而Lasso问题则无法用梯度下降算法求解,因为函数不是处处光滑,具体可参考上面给出的Norm-1的定义,所以,对于Lasso问题需要选用次梯度算法求解。
则称为Lasso回归。对于岭回归,我们仍然可以采用梯度下降算法求解目标函数,因为函数处处可导光滑,而Lasso问题则无法用梯度下降算法求解,因为函数不是处处光滑,具体可参考上面给出的Norm-1的定义,所以,对于Lasso问题需要选用次梯度算法求解。
下图是对于同样数据集下分别对逻辑回归选用岭惩罚和Lasso惩罚求解最优解的实验结果图(n=1000,p=20n=1000,p=20):
B. 随机次梯度算法
上面讲到的次梯度算法梯度更新定义为:
随机次梯度算法(Stochastic Subgradient Method)与次梯度算法(Subgradient Method)相比,每次更新次梯度是根据某一个样本计算获得,而不是通过所有样本更新次梯度,其定义为:
![]()
其中,![]() 是第
是第![]() 次迭代随机选取的样本
次迭代随机选取的样本![]() 。从该方法的定义,我们也可引出随机梯度下降算法(Stochastic Gradient Descent)的定义,即当函数
。从该方法的定义,我们也可引出随机梯度下降算法(Stochastic Gradient Descent)的定义,即当函数![]() 可微连续时,
可微连续时,![]() 。
。
所以,根据梯度更新的方式不同,次梯度算法和梯度下降算法一般被称为“batch method”。从计算量来讲,![]() 次随机更新近似等于一次batch更新,二者差别在于
次随机更新近似等于一次batch更新,二者差别在于![\sum_{i=1}^m[\nabla f(x_{i}^{(k)}) - \nabla f(x_{k_i}^{(k)})]](http://img.e-com-net.com/image/info8/fe08da07995c477a8232ac9b01eeaae5.gif) ,当
,当![]() 变化不大时,差别可以近似等于0。
变化不大时,差别可以近似等于0。
对于随机更新次梯度,一般随机的方式有两种:
- Cyclic rule:选择
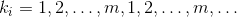 ;
; - Randomized rule:均匀随
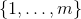 机从选取一点作为
机从选取一点作为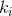 。
。
与所有优化算法一样,随机次梯度算法能否收敛?
答案是肯定的,这里就不在做证明,有兴趣的同学可以参考boyd教授的论文,这里仅给出收敛结果,如下:
对于Cyclic rule,随机次梯度算法的收敛速度为![]() ;对于Randomized rule,随机次梯度算法的收敛速度为
;对于Randomized rule,随机次梯度算法的收敛速度为![]() 。
。
下图给出梯度下降和随机梯度下降算法在同一数据下迭代结果:
随机梯度下降一般有两个特性:
- 通常下降的速度较batch方法要快。
- 通常在最优点附近会来回震荡,相较于batch方法不够稳定。
参考文章:
凸优化-次梯度算法
优化中的subgradient方法
次导数 次梯度 小结
次梯度(Subgradient)
次梯度