相关滤波跟踪·CSK算法梳理（巨详（啰）细（嗦））

从MOSSE到CSK算是了解相关滤波跟踪的必经之路了。CSK在MOSSE模型的基础上增加了正则项以避免过拟合，提出了分类器的概念，同时引入了循环矩阵和核函数提高运算速率。
答应我，看CSK或者KCF之前，请一定先去看一下SVM（支持向量机）！
顺便指路我学习SVM的整理(https://blog.csdn.net/qq_32763701/article/details/83859575)，如果你看了这个，请跳转算法部分开始看

为什么引入循环矩阵？

很多文章里解释引入循环矩阵是为了利用循环矩阵的特性达到密集采样（dense sampling）和转到频域提高运算效率的目的，但循环矩阵具体是如何达到这一目的我姑且写一下我的理解。

我们回忆一下MOSSE算法里求相关性的操作是通过在怀疑区域里滑动卷积得到的，如果是要求密集采样（而不是随机采样）的话，要求卷积模板在这一区域从第一个像素滑动到最后一个像素，在这一区域产生大量候选窗（这些候选窗重合度还很大），最终目标匹配得到最后的输出结果。这一过程明显计算量巨大，影响跟踪速度。

所以作者引进循环矩阵这个好工具：

第一行为实际采集的目标特征，其他行表示周期性地把最后的矢量依次往前移产生的虚拟目标特征。因为整个循环矩阵都是由$n\times 1$ $vector$ $\hat{u}$演变而来，所以循环矩阵不需要空间专门去保存它。这一操作的具体效果作者在15年的KCF算法里做了更直观地解释：

直接利用循环矩阵去和滤波器点乘（后面会解释）很直观地省略了卷积模板在检测区域内滑动的过程，简化了对重合度高的候选窗的运算，提高了速度。
也可以理解为滤波器模板在频域内与样本特征边缘求相关时边界循环补充的结构。
（解释见(https://blog.csdn.net/qq_17783559/article/details/82321239)）

另一方面，如上图所示，循环矩阵对像素的移动产生了目标发生上下位移的结果，可以理解为在这一帧里样本数增加了。更多的样本数意味着训练的结果更准确。

此外，循环矩阵傅里叶对角化特性也是引入循环矩阵重要的原因之一。
根据循环矩阵的特点，存在$u\otimes v=C\left(u\right)v=F^{-1}\left(F\left(u\right)\odot F\left(v\right)\right)$
利用这一特性证明循环矩阵的和、点积、求逆都是循环矩阵，在频域利用这一特性大大提高了运算速率。
（证明见(https://blog.csdn.net/shenxiaolu1984/article/details/50884830)）

为什么引入核函数？

核函数是模式识别里的一个技巧。我们知道在低维空间中线性不可分的模式可以映射到高维空间实现线性可分，比如：（参考(https://blog.csdn.net/qq_32763701/article/details/83859575)）

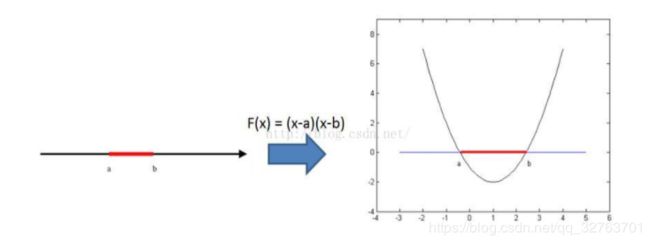
其中红线和黑线分别表示两类数据，在二维空间里线性不可分，映射到高维空间后利用二次函数（曲线）实现了可分。
但问题在于，虽然在高维空间实现了线性可分，但一是映射关系难以求解，二是在高维空间运算时，容易导致维数灾难，维数越大，计算量也指数增大。
引入核函数的目的是利用在原空间的核函数的值表示高维空间的向量的內积，简化计算。

在CSK算法的证明中，在将输入函数$\mathbf{x}$映射到高维空间后，出现高位空间内的內积项$<\phi \left(\mathbf{x}\right),\phi \left({\mathbf{x}}^{\prime }\right)>$。
核函数要实现的就是令$k\left(\mathbf{x},{\mathbf{x}}^{\prime }\right)=<\phi \left(\mathbf{x}\right),\phi \left({\mathbf{x}}^{\prime }\right)>$，把高维空间的內积转换为原空间的核函数值。

算法：核化的最小二乘法（KRLS）

首先我们回忆一下MOSSE算法的基本模型
${\min }_{H^{\ast }}{\sum }_i{\left|F_i\cdot H^{\ast }-G_i\right|}^2$
其中$F_i$是输入图像特征，$H^{\ast }$是滤波器，$G_i$表示响应，具体推导过程见前一篇文章。相关滤波跟踪·MOSSE算法的梳理

CSK算法在MOSSE模型的基础上将相关用分类器运算表示，并做了一些修改
${\min }_w{\sum }_{i}L\left(y_i,f\left({\mathbf{x}}_{\mathbf{i}}\right)\right)+\lambda {\Vert \mathbf{w}\Vert }^2$

嘛，虽然看起来各种不像，但其实化开以后本质还是一样的。

接下来进入推导过程。

一点小tips

首先，我们最好先弄懂几个小数学知识：

1.$A$是一个列向量，$${\Vert A\Vert }^2=A^T\cdot A$$
2.$A$,$B$均为列向量，$$A^T\cdot B=<A,B>$$
3.$$S=\sum _{i=1}^n{a}_i{b}_i=a_1{b}_1+a_2{b}_2+\cdots +a_n{b}_n$$
如果$A=\left[\begin{array}{c}a1\\ a_2\\ ⋮\\ a_n\end{array}\right]$，$B=\left[\begin{array}{c}b1\\ b_2\\ ⋮\\ b_n\end{array}\right]$，则$$S=A^T\cdot B$$
如果$A=\left[\begin{array}{c}a1\\ a_2\\ ⋮\\ a_n\end{array}\right]$，$B=\left[\begin{array}{ccccc}{b}_1& b_2& \cdots & & b_n\end{array}\right]$，则$$S=B\cdot A$$（行向量在前）
掌握了上述3个小技巧以后我们就可以继续勇敢地前进了！

继续*1

不管样本$X_i$是不是线性可分，将它映射到高维空间后，$\phi (X_i)$就线性可分了，也可以用线性分类器就行目标和背景的分类了。（顺便一说，下文推导中，凡是大写都是矩阵，小写都是矩阵中的元素，可能会和原文符号有所不同；还有，$i$对应的是第$i$个样本！$i$对应的是第$i$个样本！$i$对应的是第$i$个样本！）

所以根据SVM，在高维空间中滤波器（SVM的权重）可以表示为样本的线性组合。
$$\begin{array}{rl}W& ={\alpha }_1\phi (X_1)+{\alpha }_2\phi (X_2)+\cdots \\ & =\sum _{j=1}^n{\alpha }_j\phi (X_j)\end{array}$$

所以线性分类器$$\begin{array}{rl}f(X_i)& =<W,\phi (X_i)>+b\\ & =<\sum _{j=1}^n{\alpha }_j\phi (X_j),\phi (X_i)>+b\\ & =\sum _{j=1}{\alpha }_j<\phi (X_j,\phi (X_i)>+b\\ & =\sum _{j=1}^n{\alpha }_j\kappa (X_j,X_i)\\ & =\sum _{j=1}^n{\alpha }_j\kappa (X_i,X_j)\end{array}$$

其中引入核函数$\kappa (X_i,X_j)=<\phi (X_j,\phi (X_i)>$，$\kappa (X_i,X_j)$是矩阵$K$的第i行第j列。
注意到$\mathbf{\alpha }=\left[\begin{array}{c}{\alpha }_1\\ {\alpha }_2\\ ⋮\\ {\alpha }_j\end{array}\right]$，$K$的第i行为$K_i=\left[\begin{array}{cccc}\kappa (X_i,X_1)& \kappa (X_i,X_1)& \cdots & \kappa (X_i,X_j)\end{array}\right]$
同学们，请抬头看看tips里的第3项第2类！

所以，$f(X_i)=K_i\mathbf{\alpha }$，这是一个数啊同学们。

那么再来看一下正则项$$\begin{array}{rl}\frac{1}{2}{\Vert W\Vert }^2& =\frac{1}{2}{W}^{T}W\\ & \\ & =\frac{1}{2}\sum _{j=1}^n{\alpha }_j(\phi (X_j){)}^T\cdot \sum _{j=1}^n{\alpha }_j\phi (X_j)\\ & \\ & =\frac{1}{2}\sum _{j=1}^n\sum _{j=1}^n{\alpha }_j{\alpha }_j(\phi (X_j){)}^T\phi (X_j)\\ & \\ & =\frac{1}{2}\sum _{j=1}^n\sum _{j=1}^n{\alpha }_j{\alpha }_j<\phi (X_j),\phi (X_j)>\\ & \\ & =\frac{1}{2}\sum _{j=1}^n\sum _{j=1}^n{\alpha }_j{\alpha }_j{K}_{jj}\\ & \\ & ={\alpha }_1^2{K}_{11}+{\alpha }_1^2{K}_{11}+\cdots {\alpha }_n^2{K}_{nn}\\ & \\ & ={\alpha }^{T}K\alpha \end{array}$$

继续*2

所以我们前面觉得不是很明白的从SVM角度写的模型从MOSSE的角度可以理解为

（1）$L$表示最小二乘法的损失函数

$$L\left(Y_i,f\left(X_i\right)\right)={\left(Y_i-f\left(X_i\right)\right)}^2$$

很明显对应MOSSE中的方差。$Y_i$是SVM中的标签，标记样本属于哪一边。这里作为响应，对应$g_i$。

（2）线性分类器$f\left(X_i\right)$ 表示滤波器$W$和输入图像特征$\phi (X_i)$相关的结果，对应$f_i\cdot h$。

（3）模型增加了一个正则项，所以CSK的最小二乘法也被叫做正则最小二乘法，也叫岭回归。正则项增加的目的是为了排除一些循环矩阵变换后变形过度的虚拟样本。

继续*3

原模型转换为

$$min\sum _{i=1}^m(Y_i-K_i\mathbf{\alpha }{)}^2+\lambda {\mathbf{\alpha }}^{T}K\mathbf{\alpha }$$
注意${\sum }_{i=1}^m(Y_i-K_i\mathbf{\alpha }{)}^2$，抬头看看刚才小tips里第三项第一类！
令$Y=\left[\begin{array}{c}{y}_1\\ y_2\\ ⋮\\ y_m\end{array}\right]$，$K\mathbf{\alpha }=\left[\begin{array}{c}{K}_1\mathbf{\alpha }\\ K_2\mathbf{\alpha }\\ ⋮\\ K_m\mathbf{\alpha }\end{array}\right]$（K下标表示第几行）

所以上式可以化为$$min[(Y-K\mathbf{\alpha }{)}^T(Y-K\mathbf{\alpha })+\lambda {\mathbf{\alpha }}^{T}K\mathbf{\alpha }]$$

因为对$\alpha$没有约束条件，因此直接通过求导得到$\alpha$最小值。（已知$K!=0$）
$$\begin{array}{rl}& \frac{\partial }{\partial \mathbf{\alpha }}min[(Y-K\mathbf{\alpha }{)}^T(Y-K\mathbf{\alpha })+\lambda {\mathbf{\alpha }}^{T}K\mathbf{\alpha }]\\ & \\ & =min(Y-K\mathbf{\alpha }{)}^T(-K)+\lambda {\mathbf{\alpha }}^{T}K\\ & \\ & =min(K\mathbf{\alpha }-Y)+\lambda {\mathbf{\alpha }}^T=0\end{array}$$

得到
$$\begin{array}{rl}（Y-K\mathbf{\alpha }{）}^T& =\lambda {\mathbf{\alpha }}^T\\ Y-K\mathbf{\alpha }& =\lambda \mathbf{\alpha }\\ \mathbf{\alpha }& =(\lambda I+K{)}^{-1}Y\end{array}$$

继续*4

引入循环矩阵，已知循环矩阵的每一行都是上一行最后一列的元素或矢量移动到第一列，所以定义一个位移矩阵$P^i$
所以密集采样得到循环矩阵$C\left(\phi (X)\right)$，其中每一行$X_i$表示为$P^{i}X$，定义

$k_i=K_{ij}=\kappa \left(X_i,X_j\right)=\kappa \left(X,P^{i}X\right)$

因为采样的结果$\phi (X)$变成循环矩阵$C\left(\phi (X)\right)$，所以原来的$K$也改为$k_i$的循环矩阵$C\left(k\right)$简化运算。

设$$I=C\left(\delta \right),\delta ={\left[\begin{array}{ccccc}1& 0& 0& ...& 0\end{array}\right]}^T$$

$$\mathbf{\alpha }={\left(C\left(k\right)+\lambda C\left(\delta \right)\right)}^{-1}Y$$

循环矩阵的和、点积、求逆都是循环矩阵

$$\mathbf{\alpha }={\left(C\left(k+\lambda \delta \right)\right)}^{-1}Y$$

傅里叶线性变换

$$\mathbf{\alpha }={\left(C\left(F^{-1}\left(F\left(k\right)+\lambda F\left(\delta \right)\right)\right)\right)}^{-1}Y$$

循环矩阵的和、点积、求逆都是循环矩阵

$$\mathbf{\alpha }=C\left(F^{-1}\left(\frac{1}{F\left(k\right)+\lambda F\left(\delta \right)}\right)\right)Y$$

由于

$$F\left(\delta \right)=1$$
所以

$$\mathbf{\alpha }=C\left(F^{-1}\left(\frac{1}{F\left(k\right)+\lambda }\right)\right)Y$$

利用$u\otimes v=C\left(u\right)v=F^{-1}\left(F\left(u\right)\odot F\left(v\right)\right)$

$$\mathbf{\alpha }=F^{-1}\left(\frac{F\left(Y\right)}{F\left(k\right)+\lambda }\right)$$

利用以上封闭解可以在频域快速得到滤波器$W$参量$\mathbf{\alpha }$

继续*5

定位用的响应图

$$Y=F^{-1}\left(F\left(k\right)\odot F\left(\alpha \right)\right)$$

本质也是高维空间的相关操作。
推导过程如下：

知道Y是一个列向量，所以
$$Y=<W,\phi (Z)>=\sum {\alpha }_i<\phi \left(X_i\right),\phi \left(Z\right)>=K\mathbf{\alpha }$$

Z是该帧未定位（求相关之前）提取的图像特征，X是该帧二次提取的图像特征，X,Z均可为循环矩阵。

所以
$$Y=\mathbf{\alpha }C\left(k\right)$$

还是用$u\otimes v=C\left(u\right)v=F^{-1}\left(F\left(u\right)\odot F\left(v\right)\right)$

$$Y=F^{-1}\left(F\left(\mathbf{\alpha }\right)\odot F\left(k\right)\right)$$

另外，核函数有很多种，本文使用高斯核函数，可以将数据映射到无穷维，也叫做径向基函数（Radial Basis Function 简称 RBF），是某种沿径向对称的标量函数。通常定义为空间中任一点x到某一中心xc之间欧氏距离的单调函数 ，可记作 k（||x-xc||）， 其作用往往是局部的，即当x远离xc时函数取值很小。

$k=exp\left(-\frac{1}{{\sigma }^2}\left({\Vert x\Vert }^2+{\Vert x^{\prime }\Vert }^2-2F^{-1}\left(F\left(x\right)\odot F\left(x^{\prime }\right)\right)\right)\right)$

继续*6

具体的学习更新流程基本和MOSSE一样，我直接改一下MOSSE的流程图，更详细的操作参考相关滤波跟踪·MOSSE算法的梳理

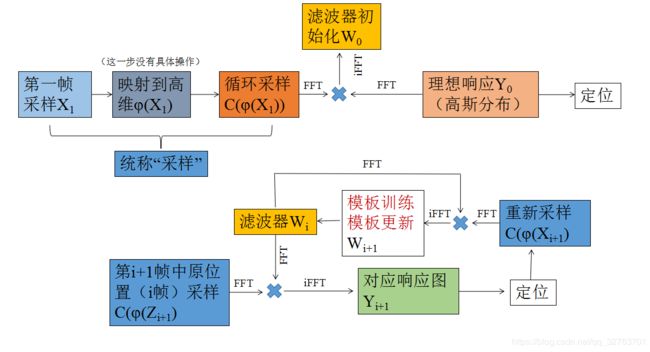
以上，欢迎交流。

[分割线181104]
※问题已解决
[分割线181109]
※重新整理了一遍