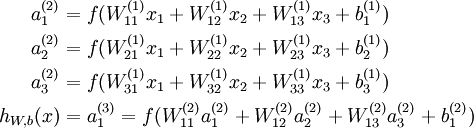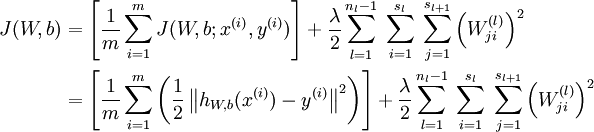UFLDL教程笔记（一）

UFLDL教程作为深度学习入门非常好的一个教程，为了防止自己看过忘过，所以写下笔记，笔记只记录了自己对于每个知识点的直观理解，某些地方加了一些使自己更容易理解的例子，想要深入了解建议自己刷一遍此教程。

一、稀疏自编码器

神经网络

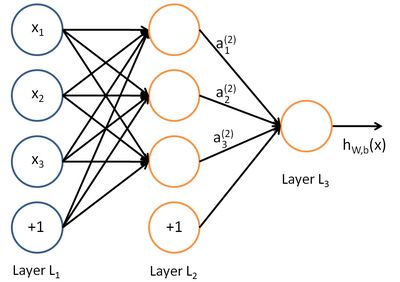
上图是一个基本的神经网络模型。我们使用圆圈来表示神经网络的输入，标上“+1”的圆圈被称为偏置节点，也就是截距项。神经网络最左边的一层叫做输入层，最右的一层叫做输出层（本例中，输出层只有一个节点）。中间所有节点组成的一层叫做隐藏层，因为我们不能在训练样本集中观测到它们的值。同时可以看到，以上神经网络的例子中有3个输入单元（偏置单元不计在内），3个隐藏单元及一个输出单元。

a(l)i 表示第 l 层第 i 单元的激活值（输出值）
W(l)ij 第 l 层第 j 单元与第l+1 层第i 单元之间的联接参数（其实就是连接线上的权重，注意标号顺序，因为W是用来计算第l+1 层的激活单元的）

下面有一个简单的前向推导过程：

反向传导神经网络

假设我们的数据是有标签的，也就是知道每个x对应的y值，现在要求权重W和偏置节点

有了输入和输出，我们只需要看我们训练的神经网络的输出结果和真实的结果的差距，然后根据误差往后一个个地更新权重（还有偏置节点）

我们首先需要将每一个参数 W 和 b 初始化为一个很小的、接近零的随机值

进行前馈传导计算，利用前向传导公式，得到L2, L3···直到输出层 Ln的激活值。

对输出层（第n层），针对第 l 层的每一个节点 i，我们计算出其“残差”，该残差表明了该节点对最终输出值的残差产生了多少影响。（于最终的输出节点，我们可以直接算出网络产生的激活值与实际值之间的差距，隐藏单元为节点残差的加权平均）

计算最终需要的偏导数值（梯度下降算法的更新需要计算代价函数的偏导数值）

注：
代价函数：

梯度下降需要更新：

自编码算法与稀疏性

这是神经网络在无监督学习中的应用

自编码神经网络是一种无监督学习算法，当在无监督学习中，有一堆没有标签的数据的时候，我们一般假设输入值与输出值基本相同，也就是x=y。或许你会问这么训练有什么意义呢？

其实可以使用自编码器来完成一些有趣的操作，如果我们有一个10X10像素的灰度图像（即n=100）。

操作1——隐层数量少于输入维度
我们用图像的灰度作为输入，即有100个输入，设隐藏层有50个，我们的输出也是图像，即输出同样是100个

此时我们训练出来的神经网络相当于具有压缩的功能，也就是说，它必须从50维的隐藏神经元激活度向量中重构出100维的像素灰度值输入x。

实上，这一简单的自编码神经网络通常可以学习出一个跟主元分析（PCA）结果非常相似的输入数据的低维表示。

操作2——隐层数量大于输入维度
这个操作中我们输入的不再是图像的灰度，而是图像整体，隐层的维度也变为100维。具体来说，如果我们给隐藏神经元加入稀疏性限制，那么自编码神经网络即使在隐藏神经元数量较多的情况下仍然可以发现输入数据中一些有趣的结构。

稀疏性限制也就是使得神经元大部分时间被限制，我们设置稀疏性参数使得隐藏神经元的平均活跃度接近一个为0的值（如0.05）

这样做有什么用呢？先来看一个已经训练完的结果

我们输入了1个图片，隐藏神经元中是100个图片，上图的每个小方块都给出了一个输入图像，它可使这100个隐藏单元中的某一个获得最大激励。

不同的隐藏单元学会了在图像的不同位置和方向进行边缘检测。

这些特征对物体识别等计算机视觉任务是十分有用的。若将其用于其他输入域（如音频），该算法也可学到对这些输入域有用的表示或特征。

二、矢量化编程

矢量化编程是提高算法速度的一种有效方法，用来提升特定数值运算操作（如矩阵相乘、矩阵相加，矩阵-向量乘法等）的运算速度。

如计算 z=θTx ，下面这种计算方法的效果就很慢：

z = 0;
for i=1:(n+1),
  z = z + theta(i) * x(i);
end;

而改成下面就会变得很快：

z = theta' * x;

为什么下面那种运算速度更快呢？因为用了matlab内部的矩阵运算策略，使用的是Intel自己出的Math kernel library（MKL）,这个库远比其他的blas/lapack库要快。

矩阵运算这块的可以参考这个链接
https://www.zhihu.com/question/19706331

三、主成分分析(PCA)与白化(Whitening )

3.1主成分分析

主成分分析（PCA）是一种能够极大提升无监督特征学习速度的数据降维算法。简单的说就是在保证有用信息尽量不丢失的情况下，尽可能的去掉无用信息。

我们希望降维后的数据尽量分散

二维降维到一维的例子

对，直接上栗子！！！

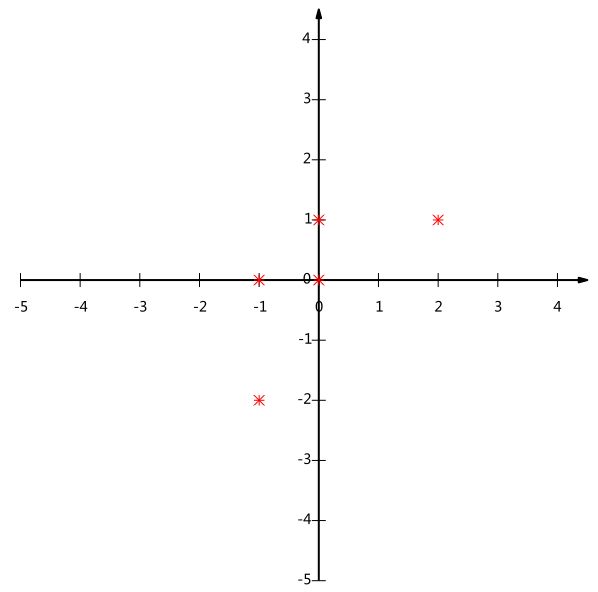
假设我们以下数据，是坐标系中的5个点的数据

(1113234424)

为了后续处理方便，我们首先将每个字段内所有值都减去字段均值，其结果是将每个字段都变为均值为0（这样做的道理和好处后面会看到）。

我们看上面的数据，第一个字段均值为2，第二个字段均值为3，所以变换后：

(−1−2−10002101)

我们可以看下五条数据在平面直角坐标系内的样子：

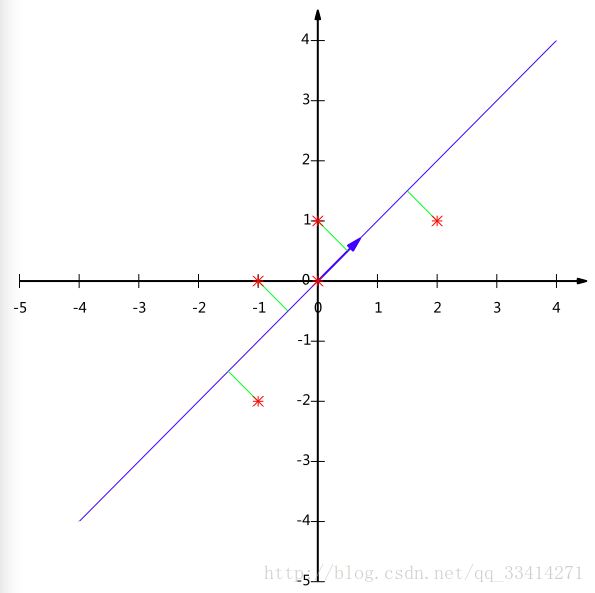
如果我们必须使用一维来表示这些数据，又希望尽量保留原始的信息，你要如何选择？

前面说过要使降维后的数据尽量分散，所以我们可以采用使方差最大的方法来找到一个直线来投影5个点。

但方差只适用于二维降到一维的情况。

数学上可以用两个字段的协方差表示其相关性，由于已经让每个字段均值为0，则：

Cov(a,b)=1m∑i=1maibi

可以看到，在字段均值为0的情况下，两个字段的协方差简洁的表示为其内积除以元素数m。

协方差矩阵的形式：

1mXXT=⎛⎝⎜⎜⎜⎜⎜1m∑i=1ma2i1m∑i=1maibi1m∑i=1maibi1m∑i=1mb2i⎞⎠⎟⎟⎟⎟⎟

所以计算得到我们的协方差矩阵为：

C=15(−1−2−10002101)⎛⎝⎜⎜⎜⎜⎜⎜−1−1020−20011⎞⎠⎟⎟⎟⎟⎟⎟=⎛⎝⎜⎜65454565⎞⎠⎟⎟

然后求其特征值和特征向量，具体求解方法不再详述，可以参考相关资料。求解后特征值为 λ1=2,λ2=2/5 ，对应的特征向量为 c1(11),c2(−11)

其中对应的特征向量分别是一个通解，c1和c2可取任意实数。那么标准化后的特征向量为：

(1/2√1/2√),(−1/2√1/2√)

将协方差举证对角化，看出那个特征向量更为重要，即应该投影到哪个直线上

可以验证协方差矩阵C的对角化：

PCPT=(1/2√−1/2√1/2√1/2√)(6/54/54/56/5)(1/2√1/2√−1/2√1/2√)=(2002/5)

最后我们用P的第一行乘以数据矩阵，就得到了降维后的表示：

Y=(1/2√1/2√)(−1−2−10002101)=(−3/2√−1/2√03/2√−1/2√)

降维投影结果如下图：

总结一下PCA的算法步骤：

设有m条n维数据。

1）将原始数据按列组成n行m列矩阵X

2）将X的每一行（代表一个属性字段）进行零均值化，即减去这一行的均值

3）求出协方差矩阵 C=1mXXT
4）求出协方差矩阵的特征值及对应的特征向量

5）将特征向量按对应特征值大小从上到下按行排列成矩阵，取前k行组成矩阵P

6） Y=PX 即为降维到k维后的数据

PCA算法详情请戳
链接：http://blog.codinglabs.org/articles/pca-tutorial.html

假设你使用图像来训练算法，因为图像中相邻的像素高度相关，输入数据是有一定冗余的。由于相邻像素间的相关性，PCA算法可以将输入向量转换为一个维数低很多的近似向量，而且误差非常小。

3.2白化

我们已经了解了如何使用PCA降低数据维度。在一些算法中还需要一个与之相关的预处理步骤，这个预处理过程称为白化（一些文献中也叫sphering）。

举例来说，假设训练数据是图像，由于图像中相邻像素之间具有很强的相关性，所以用于训练时输入是冗余的。白化的目的就是降低输入的冗余性；更正式的说，我们希望通过白化过程使得学习算法的输入具有如下性质：(i)特征之间相关性较低；(ii)所有特征具有相同的方差。

白化分为PCA白化 ZCA白化

原始数据：

PCA白化后结果：

ZCA白化后结果：

PCA白化ZCA白化都降低了特征之间相关性较低，同时使得所有特征具有相同的方差。

1. PCA白化需要保证数据各维度的方差为1，ZCA白化只需保证方差相等。

2. PCA白化可进行降维也可以去相关性，而ZCA白化主要用于去相关性。

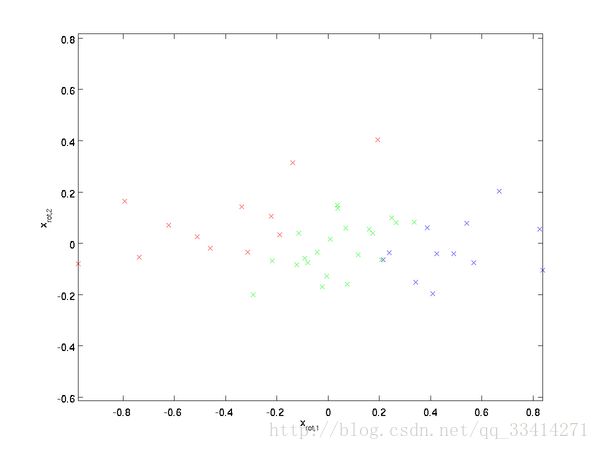
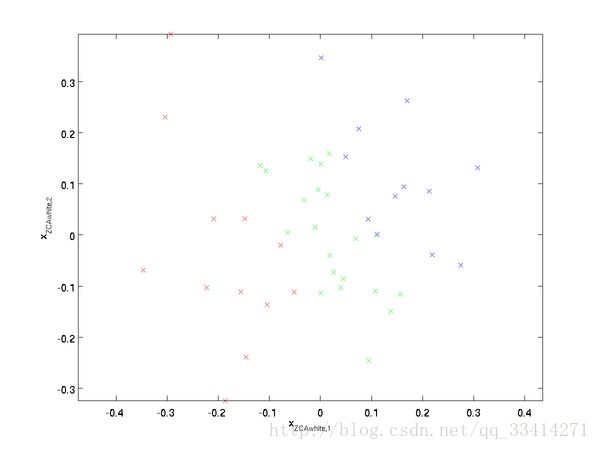
3. ZCA白化相比于PCA白化使得处理后的数据更加的接近原始数据。