快排总结和优化

快排总结和优化

---

emmm……把以后可能用到的快排和优化后的快排整理了一下。

快速排序是一种分治的算法。
与归并排序不同，归并排序是先对子数组分别排序，再归并使整个数组有序；
快速排序是不断地递归对数组进行切分，当子数组有序时整个数组也就自然有序了。

1.基本算法

基于二分法的快排，左右分别递归：

public static void quickSort(int[] array, int lo, int hi) {
    if(hi <= lo ) return;
    int pivot = partition(array, lo, hi);
    quickSort(array, lo, pivot - 1);
    quickSort(array, pivot + 1, hi);
}

---

2.切分算法

快速排序的关键在于切分算法，切分算法有多种写法。

快速切分原理图 ：

I.切分一：

原理如图，一般策略是随意选取a[lo]作为轴点v（切分元素）； 然后从左往右扫描直到找到一个大于它的元素，再从右往左扫描知道找到一个小于等于它的元素； 如此继续，直到最后i,j两个指针相遇时，再将选取的轴点v和左子数组最右侧的元素a[j]交换，然后返回j(或i)即可。

private static int partition(int[] array, int lo, int hi) {
    int i = lo, j = hi + 1;
    int pivot = array[lo];//以首元素作为候选轴点
    while(true) {
        //从左往右直到找到大于或等于pivot的元素结束
        while(array[++i] < pivot) if(i == hi) break;
        //从右往左直到找到小于或等于pivot的元素结束
        while(pivot < array[--j]) if(j == lo) break;
        if(i >= j) break;
        //交换找到的两个元素
        swap(array, i, j);
    }
    //最后将轴点的值与i,j相遇的位置的值进行交换
    swap(array, lo, j);
    return j; //此时找到轴点位置j
}

注：也可以先从右往左扫描； 这个算法中break用来检测越界，要是越界就用break退出。

II.切分二：

第二个版本（初学时写的比较多）先从右往左扫描，并且减少了swap()额外空间带来的开销，但也有些细节需要注意。

private static int partition(int[] list, int lo, int hi) {
    int pivot = list[lo];
    while(lo < hi){
        //从右往左找到小于或等于pivot的元素，h向左拓展
        while(lo < hi && pivot < list[hi]) hi--;
        if(lo < hi){
            list[lo++] = list[hi];
        }
        //从左往右找到大于pivot的元素，lo右拓展
        while(lo < hi && list[lo] < pivot) lo++;
        if(lo < hi){
            list[hi--] = list[lo];
        }
    }
    list[lo] = pivot;
    return lo;
}

这里面加if语句是为了，防止lo大于hi时hi（lo）继续拓展，如果不加这句,它的上一句改成pivot<=list[hi],它的下一句需要去掉++，之所以这样写是为了减少防止有大量重复元素时，由于过多的拓展，时间复杂度退化为O( n2 )，但同时也增加了交换次数，使快排的稳定性更难保持，这是一个小细节。

---

3.基本快排的补充

• 原地切分：使用一个辅助数组来辅助，但切分后的数组复制回去的开销会大很多。
• 保持随机性：快排是依赖输入的算法，快排的开始前可以写一个shffle()方法将数组打乱,或直接可以写:

Random rnd = new Random();
int index = rnd.nextInt(array.length);
swap(array, pivot, index);

开始时用来随机选取轴点，避免快排对输入的依赖。

• 避免等值元素的交换：实现快排时要做到这点，不然时间复杂度会退化到O( n2 )。

• 递归的终止：实现快排的常见错误是不能将轴点放入正确位置，就会导致程序在轴点正好是子数组的最大或最小元素时陷入无限循环。

---

4.性能特点

对于长度为n的无重复数组，快排平均需要~ 2nlnn （ 1.39nlogn ）次比较，以及 1/6 次交换；
快排最多需要 n2/2 次比较，但随机打乱数组能避免这种情况。

---

5.快排的改进

I.小数组切换到插入排序

对小数组快速排序比插入排序慢，还有递归调用，因此以在快排的过程中遇到小数组时应该切换到插入排序。

将quickSort()中的语句：if(hi <= lo) return;
替换为：if(hi <= lo + M) { insertionSort(a, lo, hi); return; }
转换参数M的最佳值与系统相关，但在5~15之间的任意值在大多数情况下都能令人满意。

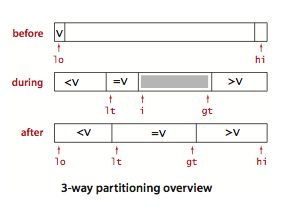
II.三向切分快排

对于有大量重复元素的数组，这种方法比标准的快速排序的效率要高很多

三向切分快排原理图：

三向切分快排思路跟普通快排差不多，只是把轴点变成了“轴线”，“轴线”部分的值就是轴点值，大的元素放到轴点值右边，小的元素放在轴点值左边。
实现时，每次都让lt下标的值等于轴点值，用i扫秒lt右侧，碰到与轴点相等的值就继续向后扫描，这样就使得中间部分的元素值都等于轴点值了。也就是说工作指针 i 经过的地方都等于轴点值。
切分结束的条件也跟普通快排差不多，当i的位置大于gt的位置就结束算法。
跟普通快排一样是小值扔轴点左边，大值扔轴点右边。

public static void quick3waySort(int[] array, int lo, int hi) {
    if(hi <= lo) return;
    int lt = lo, i = lo + 1, gt = hi;
    int pivot = array[lo];//轴点取最低位
    //一次切分
    while(i <= gt) {
        //i处的值小于轴点就与lt交换，并继续向后扫描，同时lt也右移
        if      (array[i] < pivot) swap(array, lt++, i++);
        //i处的值大于轴点就和gt交换，然后gt左移
        else if (array[i] > pivot) swap(array, i, gt--);
        //碰到与轴点相等的值继续向后扫描
        else                       i++;
    }
    quick3waySort(array, lo, lt - 1);
    quick3waySort(array, gt + 1, hi);
}

III.双轴点快排

还有一种和三向切分快排类似的双轴快排，Arrays.sort()就主要是用它来实现的。
与三向切分快排不同的是，双轴快排的两个轴分别为lo, hi。
在双轴快排中部即工作指针 i 扫描过的地方比左轴点的值大，比右轴点的值小，但仍然无序。

  private static void dualpivotQuickSort(int[] array, int lo, int hi) { 
        if (hi <= lo) return;

        //开始划分前确保a[lo] <= a[hi]
        if (array[hi] < array[lo]) swap(array, lo, hi);

        int lt = lo + 1, gt = hi - 1;
        int i = lo + 1;
        //一次切分
        while (i <= gt) {
            //i处的值小于左轴点就与lt交换，并继续向后扫描，同时lt也右移
            if       (array[i] < array[lo]) swap(array, lt++, i++);
            //i处的值大于右轴点就和gt交换，然后gt左移
            else if  (array[hi] < array[i]) swap(array, i, gt--);
            else                    i++;
        }
        //一次切分结束后在序列中间得到一个小值和大值，让他们分别和两轴点交换
        swap(array, lo, --lt);
        swap(array, hi, ++gt);

        dualpivotQuickSort(array, lo, lt-1);
        //如果中部序列低位的值小于高位的值，那就也对它进行快排
        if (array[lt] < array[gt]) dualpivotQuickSort(array, lt+1, gt-1);
        dualpivotQuickSort(array, gt+1, hi);
    }

6.其他

快排的优化还有很多，还有三轴点快排可以参考论文：http://epubs.siam.org/doi/pdf/10.1137/1.9781611973198.6
关于JDK里Arrays.sort()的源码分析就参考这个大神啦：http://www.jianshu.com/p/6d26d525bb96
还可以参考这个：http://blog.csdn.net/holmofy/article/details/71168530

---