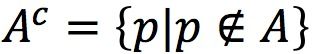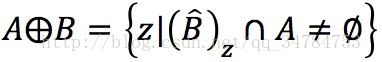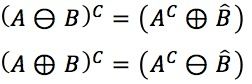【OpenCV图像处理】十八、数学形态学方法(上)
数学形态学是以形态表示为基础实现图像分析的数学工具,使用具有一定形态的结构元素去度量和提取图像中对应形状,以此来达到对图像分析和识别的目的。形态学图像处理的数学基础是集合论,主要的运算包括腐蚀、膨胀、开运算、闭运算四种。
数学形态学方法进行图像处理的基本思想是选择具有一定尺寸和形状的结构元素度量并提取图像中相关形状结构的图像分量,以此来达到对图像分析和识别的目的。需要注意的是,数学形态学方法可以用于二值图像和灰度图像的处理和分析。
利用数学形态学处理图像的优点如下:
①进行图像复原时,我们可以借助先验的几何特征信息,利用形态学算子有效消除噪声,又可以保留图像的原有信息。
②进行边缘信息提取时,对噪声不敏感,能够得到光滑的边缘结果
③对图像进行骨架提取时,也能够得到比较连续的结果
④算法便于使用硬件进行实现
1.集合运算
在讨论二值图像的形态学操作时,我们将二值图像看成是其中所有的“1”像素构成的集合。
下面使用集合A表示二值图像,元素p表示“1”像素在二值图像中的坐标(x, y),所以,元素p属于集合A是指p是集合A中的元素,记为
p ∈ A
(a.并集,交集,差集和补集
(1.并集:A∪B = {p| p∈A or p∈B }
A∪B 中的元素属于A或是属于B
(2.交集:A∩B = {p| p∈A and p∈B }
A∪B 中的元素既属于A也属于B
(3.补集:不在集合A中的元素构成A的补集
(4.差集:A-B 即为在集合A中,但是不在集合B中的元素
(b.平移和映射
集合A映射构成的集合,记做 Â
 = {p | p = -q,q ∈ A}
集合A的映射集合Â包含的元素为集合A中的每个坐标关于原点镜像坐标
集合A平移z构成的集合记做(A)z
(A)z = {p | p = q+z,q ∈ A}
(A)z包含的元素为集合A中的每一个坐标与位移![]() 相加而形成的新坐标。
相加而形成的新坐标。
2.二值图像的逻辑运算
集合的运算与逻辑运算具有一一对应的关系
也就是说,集合的补集运算对应逻辑非,集合并集对应逻辑或,交集对应于逻辑与。
3.结构元素
在二值图像形态学中,结构元素是一个由0值和1值组成的矩阵,每个结构元素有1个原点,结构元素中的原点指定待处理像素的位置,结构元素中的1定义了结构元素的邻域。
输出图像中对应原点的值建立在输入图像中相应像素与及其邻域像素比较的基础上。在本文中,“1”代指白色,“0”代指黑色
通常情况下,将结构元素中心位置指定为原点。
4.二值图像的形态学基本运算
在二值图像形态学运算过程中,将二值图像和结构元素均看成是集合。
因此二值图像形态学运算时使用结构元素B对二值图像A进行的操作,在通常情况下,二值图像形态学运算是对二值图像中“1”像素区域进行的
(1.膨胀操作
结构元素B对集合A的膨胀,定义为:
结构元素B对集合A的膨胀过程为:
(①将结构元素B关于原点的映射(B)平移z
(②几个A与结构元素B的映射平移(B)z的交集不为空集
B对A膨胀生成的集合是B的映射平移集合与集合A至少有1个非0元素时B的原点位置的集合
膨胀操作的作用:
膨胀运算具有扩张目标区域的作用。
→对于原点属于结构元素的膨胀运算,![]() 总是成立
总是成立
对于原点不属于结构元素的膨胀运算,![]() 不一定成立
不一定成立
→对于一幅二值图像,膨胀运算可以扩张白色目标区域,填补目标区域中尺寸小于结构元素的孔洞和缺口。
(2.腐蚀操作
结构元素B对集合A的腐蚀,记做![]() ,定义为:
,定义为:
腐蚀过程为:
→将节后元素B平移后仍完全包含在集合A中
→B对A腐蚀生成的集合是B的平移集合完全包含在集合A中B的原点位置的集合。
腐蚀操作的作用:
腐蚀运算具有收缩目标区域的作用
→对于原点属于结构元素的腐蚀运算,![]() 总是成立
总是成立
→对于原点不属于结构元素的腐蚀运算,![]() 不一定成立
不一定成立
→对于一幅二值图像,腐蚀运算可以收缩白色的目标区域,消除了储存小于结构元素的目标和毛刺。
(3.膨胀和腐蚀操作的对偶性
将图像的腐蚀操作的定义改写为如下形式:
与膨胀的定义相对比可以发现
→对图像中目标区域的膨胀运算相当于对背景区域的腐蚀,反之亦然
→图像的膨胀与腐蚀是一对互为对偶的运算操作
这种对偶性可以表示为:
由对偶性可以表明:二值图像形态学的基本运算本质上只有一个
→整个二值图像形态学体系建立在一个基本运算的基础之上。
5.使用OpenCV实现膨胀和腐蚀
在OpenCV中可以方便地使用erode()函数和dilate()函数来实现上面提到的腐蚀和膨胀的操作。
下面分别介绍这两个函数的定义
腐蚀函数如下:
void erode( InputArray src, OutputArray dst, InputArray kernel,Point anchor=Point(-1,-1), int iterations=1,
int borderType=BORDER_CONSTANT,const Scalar& borderValue=morphologyDefaultBorderValue() );void dilate( InputArray src, OutputArray dst, InputArray kernel,Point anchor=Point(-1,-1), int iterations=1,
int borderType=BORDER_CONSTANT, const Scalar& borderValue=morphologyDefaultBorderValue() );上面两个函数分别表示使用一个特定的结构化元素腐蚀一个图像和使用图像结构化元素对图像进行腐蚀和膨胀。
参数src表示输入图像,为二值图像或灰度图像;
参数dst表示输出图像,参数类型和输入图像一致;
参数kernel表示定义的结构元素的大小,当这个参数为NULL时,表示的是使用参考点位于中心3x3的核
(→通常,我们一般使用函数getStructuringElement配合这个参数的使用。getStructuringElement函数会返回指定形状和尺寸的结构元素(内核矩阵)。其中,getStructuringElement
函数的第一个参数表示内核的形状,有下面三种形状可以选择
(·矩形:MORPH_RECT;
(·交叉形:MORPH_CROSS;
(·椭圆形:MORPH_ELLIPSE;
而getStructuringElement函数的第二和第三个参数分别是内核的尺寸以及锚点的位置。
一般在调用这两个函数之前,首先定义一个Mat类型的变量来获得getStructuringElement函数的返回值。对于锚点的位置,有默认值Point(-1,-1),
表示的是锚点位于中心,此外,需要注意的是,十字形的element形状唯一依赖于锚点的位置,而在其他情况下,锚点只是影响了形态学运算结果的偏移。
使用的例子如下:
//获取自定义核
Mat element = getStructuringElement(MORPH_RECT,Size(15,15));参数anchor表示结构元素的中心,如果是默认参数(-1,-1),程序会自动将其设置为结构元素的中心;
参数iterations表示迭代次数,我们可以选择对图像进行多次形态学运算
最后两个参数borderType和borderValue为可以选择参数设置,针对边界进行设置。
具体程序如下所示:
#include
#include
#include
#include
using namespace cv;
using namespace std;
int main()
{
Mat srcImage = imread("2345.jpg", 0);
if (!srcImage.data)
{
cout << "读入图片错误" << endl;
system("pause");
return -1;
}
Mat srcBinary;
threshold(srcImage, srcBinary, 0, 255, THRESH_OTSU);
imshow("原始图像", srcBinary);
//获取自定义核
Mat element = getStructuringElement(MORPH_RECT, Size(15, 15));
Mat ErodeImage;
Mat DilateImage;
erode(srcBinary, ErodeImage, element);
imshow("腐蚀效果图", ErodeImage);
dilate(srcBinary, DilateImage, element);
imshow("膨胀效果图", DilateImage);
waitKey();
return 0;
} 执行程序后,效果如下所示:
6.开运算与闭运算
(1.开运算
开运算为先对图像进行腐蚀后再进行膨胀的运算,结构元素对集合A的开运算,记做AoB,定义为
![]()
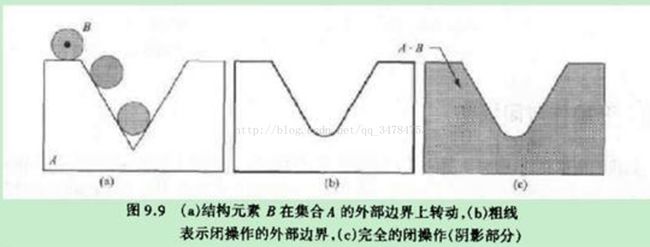
→开运算可以消除小尺寸的目标和细小的突出部分,断开细长的桥接部分从而分离出目标区域,并在不明显改变目标区域面积的条件下平滑较大目标边界的作用。
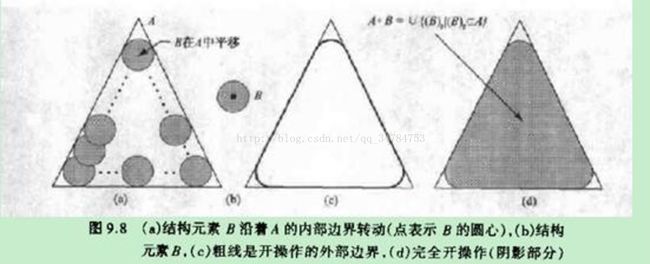
→设有结构元素B和集合A,则开运算的实质就是让B在A的区域内部全部平移,可以表示为
![]()
其中U{·}表示的是括号中全部集合的并集运算,图示如下:
(2.闭运算
闭运算为先对图像进行膨胀后在腐蚀的运算,结构元素B对集合A的闭运算记做:A•B,定义如下:
![]()
→闭运算可以填补目标区域内部小尺寸孔洞和细窄的缺口,桥接狭窄的断裂部分从而使目标区域变得连通,并且可以再不明显改变目标区域面积的条件下平滑较大目标边界的作用。
→从几何意义上讲,对于结构元素B,当且仅当包括元素p的任何平移集合(B)z∩A≠∅时,p属于集合A•B
→图示如下:
(3.开运算与闭运算的对偶性
→开运算与闭运算也同样具有对偶性,可以表示如下:
→开运算与闭运算的结合同时具有开运算和闭运算的作用
→开运算具有消除尺寸小于结构元素的孤立目标和突起的作用
→闭运算填补了目标区域内部尺寸小于节后元素的孔洞和缺口
→开运算与闭运算的结合经常用于二值图像的后处理阶段,整个过程消除了二值图像中的孤立目标,并且填补了目标区域的内部孔洞。
→但是这两种运算会破坏目标原本轮廓和形状,特别是对于小尺寸目标会变得十分明显。
(4.使用OpenCV实现开运算和闭运算
在OpenCV中主要是使用morphologyEx()函数来实现基本的和更高级的形态学变换,如开运算,闭运算,形态学梯度,顶帽,黑帽等,下面首先简单介绍一下这个函数
函数声明如下:
void morphologyEx( InputArray src, OutputArray dst,int op, InputArray kernel,Point anchor=Point(-1,-1), int iterations=1,
int borderType=BORDER_CONSTANT,const Scalar& borderValue=morphologyDefaultBorderValue() );第二个参数dst,也就是目标图像,是函数的输出参数,需要和原图片有一样的尺寸和类型
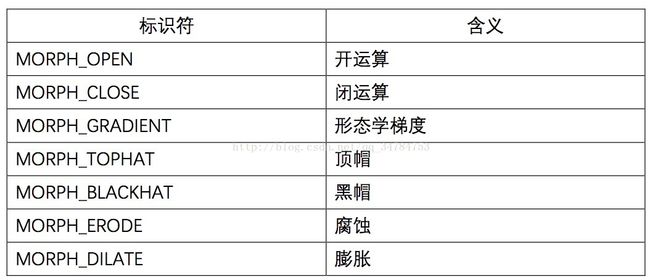
第三个参数是int类型的op,表示的是形态学运算的类型,可以是下面中的任意一个标识符:
第四个参数kernel表示形态学运算的内核。如果为NULL,表示的是使用参考点位于中心3x3的核,一般使用函数getStructuringElement()函数配合这个参数的使用。在上面讲解腐蚀膨胀函数时已经详细给出,这里不再进行赘述。
第五个参数Point类型的anchor表示锚的位置,有默认值(-1,-1),表示位于中心。
第六个参数为int类型的iterations,表示迭代使用函数的次数,有默认值1。
最后两个参数为与边界有关的参数,通常情况下直接是用默认值即可。
具体实现程序如下:
//实现形态学开运算和闭运算
#include
#include
#include
#include
using namespace cv;
using namespace std;
int main()
{
Mat srcImage = imread("2345.jpg",0);
Mat BinaryImage;
threshold(srcImage, BinaryImage, 0, 255, THRESH_OTSU);
imshow("原图像", BinaryImage);
//定义结构元素
Mat element = getStructuringElement(MORPH_ELLIPSE, Size(15, 15));
//形态学闭运算
Mat closeImage;
morphologyEx(BinaryImage, closeImage, MORPH_CLOSE, element);
imshow("闭运算操作", closeImage);
//形态学开运算
Mat openImage;
morphologyEx(BinaryImage, openImage, MORPH_OPEN, element);
imshow("开运算操作", openImage);
waitKey();
return 0;
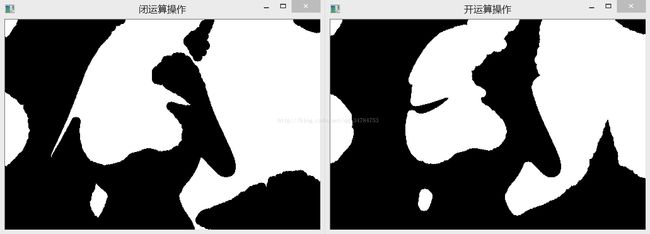
} 结构元素各向同性的开运算操作主要用于消除图像中小于结构元素的细节部分,物体的局部形状不变。物体较背景明亮时能够排除小区域物体,消除高于邻近点的孤立点,达到去噪的作用,可以平滑物体的轮廓,断开比较窄的狭颈。
而形态学闭操作能够排除小型黑洞(黑色区域),消除低于邻近点的孤立点,达到去噪的作用,可以平滑物体轮廓,弥合较窄的间断和细长的沟壑,消除小孔洞,填补轮廓线中的断裂。