机器学习习题(13)
今天主要是对于特征选择、降维方法、集成方法、做了较多的讲解。
1.机器学习中做特征选择时,可能用到的方法有?
A.卡方
B. 信息增益
C. 平均互信息
D. 期望交叉熵
E. 以上都有
参考答案:E
解析:特征选择是机器学习框架中的比较重要的一环,可以说是仅次于模型选择。上面4种是常用的文本数据的特征选择方法,还有文档频率和文本证据权(WET)等。但是除去文本的特征选择方法,还有其他类型的特征选择方法:
- WOE、IV
- Gini指数
- 相关性
- Lasso
- 距离
- 正则化
等等,结合SKlearn,详细的可以参考《SKlearn特征选择实例》。
- 下列方法中,不可以用于特征降维的方法包括()
A. 主成分分析PCA
B. 线性判别分析LDA
C. 深度学习SparseAutoEncoder
D. 矩阵奇异值分解SVD
E. 最小二乘法LeastSquares
参考答案:E
解析:
特征降维方法主要有:PCA,LLE,Isomap
SVD和PCA类似,也可以看成一种降维方法。
LDA:线性判别分析,可用于降维。
AutoEncoder:AutoEncoder的结构与神经网络的隐含层相同,由输入L1,输出 L2组成,中间则是权重连接。Autoencoder通过L2得到输入的重构L3,最小化L3与L1的差别 进行训练得到权重。在这样的权重参数下,得到的L2可以尽可能的保存L1的信息。
Autoencoder的输出L2的维度由输出的神经元个数决定。当输出维度大于L1时,则需要在训练目标函数中加入sparse 惩罚项,避免L2直接复制L1(权重全为1)。所以称为sparseAutoencoder( Andrew Ng提出的)。
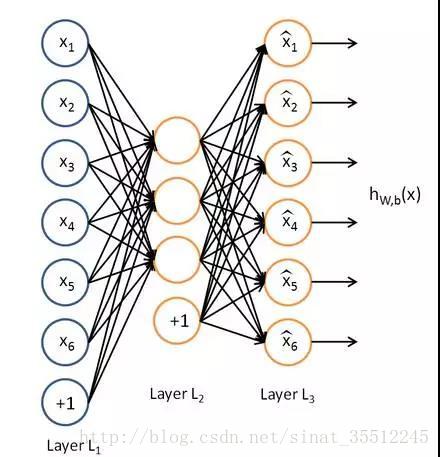
有的参考答案是把C作为答案的,但是一般来讲L2(隐含层)的维度要小于L1(输入层)的,因此应当可以认为是降维了,因为其目标就是学习一个L2.
最小二乘法是用来回归的。
3.一般,k-NN最近邻方法在( )的情况下效果较好。
A. 样本较多但典型性不好
B. 样本较少但典型性好
C. 样本呈团状分布
D. 样本呈链状分布
参考答案: B
解析:
K近邻算法主要依靠的是周围的点,因此如果样本过多,那肯定是区分不出来的。因此应当选择B。
样本呈团状颇有迷惑性,这里应该指的是整个样本都是呈团状分布,这样kNN就发挥不出其求近邻的优势了,整体样本应该具有典型性好,样本较少,比较适宜。
4.下列哪些不特别适合用来对高维数据进行降维?
A.LASSO
B.主成分分析法
C.聚类分析
D.小波分析法
E.线性判别法
F.拉普拉斯特征映射
参考答案:C
解析:
lasso在特征选择时就看到了,确实可以用来降维。
主成分分析法(PCA)和线性判别法(Fisher or LDA)都是常用的降维方法。
小波分析法的有一些变换的操作降低其他干扰可以看做是降维。
拉普拉斯特征映射将处于流形上的数据,在尽量保留原数据间相似度的情况下,映射到低维下表示。

求解广义特征向量,取前几个非零最小特值对应的特向,即为原数据在低维下的表示。
聚类分析只是无监督学习的一种方法,做不到降维。
更多详情,请参考《常用的降维方法》。
5.下面哪个选项中哪一项属于确定性算法?()
A.PCA
B.K-Means
C. 以上都不是
参考答案:A
解析:确定性算法表明在不同运行中,算法输出并不会改变。如果我们再一次运行算法,PCA 会得出相同的结果,而 K-Means 不会。除此之外,常用的机器学习算法均是确定性算法,而深度学习则不是。
6.你正在使用带有 L1 正则化的 logistic 回归做二分类,其中 C 是正则化参数,w1 和 w2 是 x1 和 x2 的系数。当你把 C 值从 0 增加至非常大的值时,下面哪个选项是正确的?()
A. 第一个 w2 成了 0,接着 w1 也成了 0
B. 第一个 w1 成了 0,接着 w2 也成了 0
C. w1 和 w2 同时成了 0
D. 即使在 C 成为大值之后,w1 和 w2 都不能成 0
参考答案:B
解析:其实这个还真是有困惑的,真正的解析应当如下图:
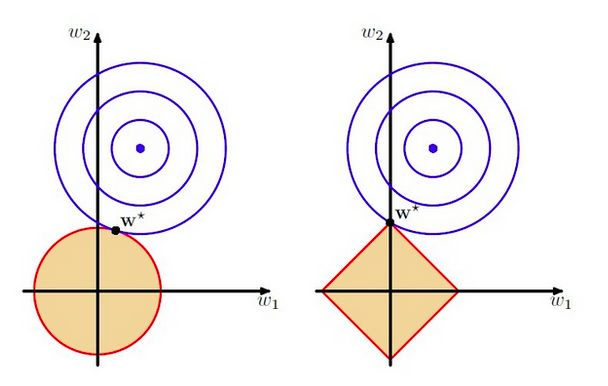
左边是L2,右边是L1。而两者的数学表示为:

这是L1,下面是L2的。

而所谓的C其实是L1正则化中的 α ,C越大,圈越小。因此可以知道C非常大的时候,W1和W2同时为0。
详细的解答请参考《防止过拟合的方法》与《L1和L2正则化的直观理解》。
- 以下说法中正确的是()
A. SVM对噪声(如来自其他分部的噪声样本)具备鲁棒性
B. 在adaboost算法中,所有被分错样本的权重更新比例相同
C. boosting和bagging都是组合多个分类器投票的方法,二者都是根据单个分类器的正确率确定其权重
D. 给定n个数据点,如果其中一半用于训练,一半用户测试,则训练误差和测试误差之间的差别会随着n的增加而减少
参考答案:C
解析:
A,软间隔是对噪声有鲁棒性的。
B,AdaBoost,是英文”Adaptive Boosting”(自适应增强)的缩写,由Yoav Freund和Robert Schapire在1995年提出。它的自适应在于:前一个基本分类器分错的样本会得到加强,加权后的全体样本再次被用来训练下一个基本分类器。同时,在每一轮中加入一个新的弱分类器,直到达到某个预定的足够小的错误率或达到预先指定的最大迭代次数。
具体说来,整个Adaboost 迭代算法就3步:
- 初始化训练数据的权值分布。如果有N个样本,则每一个训练样本最开始时都被赋予相同的权值:1/N。
- 训练弱分类器。具体训练过程中,如果某个样本点已经被准确地分类,那么在构造下一个训练集中,它的权值就被降低;相反,如果某个样本点没有被准确地分类,那么它的权值就得到提高。然后,权值更新过的样本集被用于训练下一个分类器,整个训练过程如此迭代地进行下去。
- 将各个训练得到的弱分类器组合成强分类器。各个弱分类器的训练过程结束后,加大分类误差率小的弱分类器的权重,使其在最终的分类函数中起着较大的决定作用,而降低分类误差率大的弱分类器的权重,使其在最终的分类函数中起着较小的决定作用。换言之,误差率低的弱分类器在最终分类器中占的权重较大,否则较小。
C.参见选项B
D.我们所需要的足够的数据才能够训练出好的模型,不是么?
这里要提一下C里的集成学习:
bagging:bootstrap aggregating的缩写。让该学习算法训练多轮,每轮的训练集由从初始的训练集中随机取出的n个训练倒组成,初始训练例在某轮训练集中可以出现多次或根本不出现训练之后可得到一个预测函数序列,最终的预测函数H对分类问题采用投票方式,对回归问题采用简单平均方法对新示例进行判别。
训练R个分类器,分类器之间其他相同就是参数不同。
对于新文档d,用这R个分类器去分类,得到的最多的那个类别作为d的最终类别.
boosting:其中主要的是AdaBoost(AdaptiveBoosting)。初始化时对每一个训练例赋相等的权重1/n,然后用该学算法对训练集训练t轮,每次训练后,对训练失败的训练例赋以较大的权重,也就是让学习算法在后续的学习中集中对比较难的训练铡进行学习,从而得到一个预测函数序列,预测效果好的预测函数权重较大,反之较小。最终的预测函数H对分类问题采用有权重的投票方式,对回归问题采用加权平均的方法对新示例进行判别。(类似Bagging方法,但是训练是串行进行的,第k个分类器训练时关注对前k-1分类器中错分的文档,即不是随机取,而是加大取这些文档的概率).
Rand forest: 随机森林,顾名思义,是用随机的方式建立一个森林,森林里面有很多的决策树组成,随机森林的每一棵决策树之间是没有关联的。在得到森林之后,当有一个新的输入样本进入的时候,就让森林中的每一棵决策树分别进行一下判断,看看这个样本应该属于哪一类(对于分类算法),然后看看哪一类被选择最多,就预测这个样本为那一类。
在建立每一棵决策树的过程中,有两点需要注意 - 采样与完全分裂。首先是两个随机采样的过程,random forest对输入的数据要进行行、列的采样。对于行采样,采用有放回的方式,也就是在采样得到的样本集合中,可能有重复的样本。假设输入样本为N个,那么采样的样本也为N个。这样使得在训练的时候,每一棵树的输入样本都不是全部的样本,使得相对不容易出现over-fitting。然后进行列采样,从M个feature中,选择m个(m << M)。之后就是对采样之后的数据使用完全分裂的方式建立出决策树,这样决策树的某一个叶子节点要么是无法继续分裂的,要么里面的所有样本的都是指向的同一个分类。一般很多的决策树算法都一个重要的步骤 - 剪枝,但是这里不这样干,由于之前的两个随机采样的过程保证了随机性,所以就算不剪枝,也不会出现over-fitting。 按这种算法得到的随机森林中的每一棵都是很弱的,但是大家组合起来就很厉害了。
Bagging与Boosting的区别:
- Bagging的训练集的选择是随机的,各轮训练集之间相互独立,而Boostlng的训练集的选择是独立的,各轮训练集的选择与前面各轮的学习结果有关;
- Bagging的各个预测函数没有权重,而Boosting是有权重的;
- Bagging的各个预测函数可以并行生成,而Boosting的各个预测函数只能顺序生成。对于象神经网络这样极为耗时的学习方法。
- Bagging可通过并行训练节省大量时间开销。
Rand forest与bagging的区别:
- Rand forest是选与输入样本的数目相同多的次数(可能一个样本会被选取多次,同时也会造成一些样本不会被选取到),而bagging一般选取比输入样本的数目少的样本;
- bagging是用全部特征来得到分类器,而rand forest是需要从全部特征中选取其中的一部分来训练得到分类器; 一般Rand forest效果比bagging效果好!
8.对于k折交叉验证, 以下对k的说法正确的是 :(D)
A. k越大, 不一定越好, 选择大的k会加大评估时间
B. 选择更大的k, 就会有更小的bias (因为训练集更加接近总数据集)
C. 在选择k时, 要最小化数据集之间的方差
D. 以上所有
参考答案:D
k越大, bias越小, 训练时间越长. 在训练时, 也要考虑数据集间方差差别不大的原则. 比如, 对于二类分类问题, 使用2-折交叉验证, 如果测试集里的数据都是A类的, 而训练集中数据都是B类的, 显然, 测试效果会很差。所以一般在做交叉验证时,也有使用标签按比例分配原则。
对于Bias和variance,参考下图(七月在线给出的解析实在是不明确呀):
详情参见《Bias,Error,Variance详解》
9.下图是同一个SVM模型, 但是使用了不同的径向基核函数的gamma参数, 依次是g1, g2, g3 , 下面大小比较正确的是 :
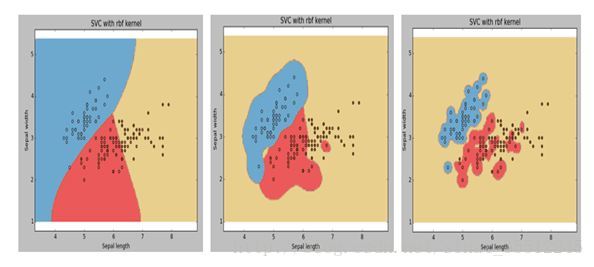
A. g1 > g2 > g3
B. g1 = g2 = g3
C. g1 < g2 < g3
D. g1 >= g2 >= g3
E. g1 <= g2 <= g3
参考答案: C
解析:gamma越小,模型越简单,平滑度越好。