Neural-style-tf
文章目录
- Pretrained VGG-19 Model
- Neural Style
- 内容损失
- 风格损失
- 定义风格
- Gram 矩阵
- 计算
- 总损失
- 总结
Pretrained VGG-19 Model
VGG在2014年的 ILSVRC localization and classification 两个问题上分别取得了第一名和第二名。VGG-19是其中的一个模型,官网上提供了预先训练好的系数,经常被业界用来做原始图片的特征变换。
VGG-19共有19层,基本结构如下:

前几层为卷积和maxpool的交替,每个卷积包含多个卷积层,最后面再紧跟三个全连接层。具体而言,第一个卷积包含2个卷积层,第二个卷积包含2个卷积层,第三个卷积包含4个卷基层,第四个卷积包含4个卷积层,第五个卷积包含4个卷基层,所以一共有16个卷积层,加上3个全连接层,一共19层,因此称为VGG-19模型。VGG-19的神经网络结构如下表所示:
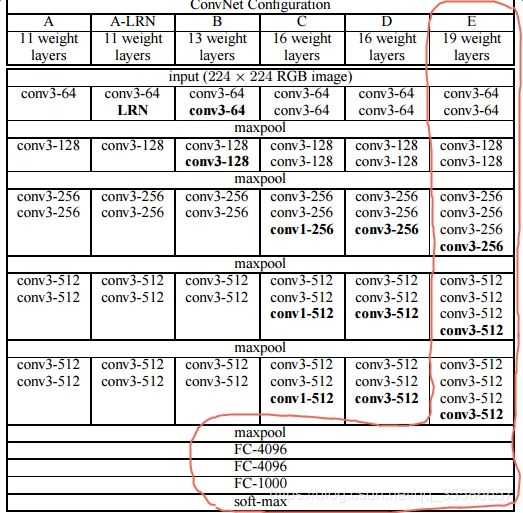
作者使用官方提供的imagenet-vgg-verydeep-19模型,实际应用中只使用卷积层,结构如下:
BUILDING VGG-19 NETWORK
loading model weights...
constructing layers...
LAYER GROUP 1
--conv1_1 | shape=(1, 512, 512, 64) | weights_shape=(3, 3, 3, 64)
--relu1_1 | shape=(1, 512, 512, 64) | bias_shape=(64,)
--conv1_2 | shape=(1, 512, 512, 64) | weights_shape=(3, 3, 64, 64)
--relu1_2 | shape=(1, 512, 512, 64) | bias_shape=(64,)
--pool1 | shape=(1, 256, 256, 64)`
LAYER GROUP 2
--conv2_1 | shape=(1, 256, 256, 128) | weights_shape=(3, 3, 64, 128)
--relu2_1 | shape=(1, 256, 256, 128) | bias_shape=(128,)
--conv2_2 | shape=(1, 256, 256, 128) | weights_shape=(3, 3, 128, 128)
--relu2_2 | shape=(1, 256, 256, 128) | bias_shape=(128,)
--pool2 | shape=(1, 128, 128, 128)`
LAYER GROUP 3
--conv3_1 | shape=(1, 128, 128, 256) | weights_shape=(3, 3, 128, 256)
--relu3_1 | shape=(1, 128, 128, 256) | bias_shape=(256,)
--conv3_2 | shape=(1, 128, 128, 256) | weights_shape=(3, 3, 256, 256)
--relu3_2 | shape=(1, 128, 128, 256) | bias_shape=(256,)
--conv3_3 | shape=(1, 128, 128, 256) | weights_shape=(3, 3, 256, 256)
--relu3_3 | shape=(1, 128, 128, 256) | bias_shape=(256,)
--conv3_4 | shape=(1, 128, 128, 256) | weights_shape=(3, 3, 256, 256)
--relu3_4 | shape=(1, 128, 128, 256) | bias_shape=(256,)
--pool3 | shape=(1, 64, 64, 256)
LAYER GROUP 4
--conv4_1 | shape=(1, 64, 64, 512) | weights_shape=(3, 3, 256, 512)
--relu4_1 | shape=(1, 64, 64, 512) | bias_shape=(512,)
--conv4_2 | shape=(1, 64, 64, 512) | weights_shape=(3, 3, 512, 512)
--relu4_2 | shape=(1, 64, 64, 512) | bias_shape=(512,)
--conv4_3 | shape=(1, 64, 64, 512) | weights_shape=(3, 3, 512, 512)
--relu4_3 | shape=(1, 64, 64, 512) | bias_shape=(512,)
--conv4_4 | shape=(1, 64, 64, 512) | weights_shape=(3, 3, 512, 512)
--relu4_4 | shape=(1, 64, 64, 512) | bias_shape=(512,)
--pool4 | shape=(1, 32, 32, 512)
LAYER GROUP 5
--conv5_1 | shape=(1, 32, 32, 512) | weights_shape=(3, 3, 512, 512)
--relu5_1 | shape=(1, 32, 32, 512) | bias_shape=(512,)
--conv5_2 | shape=(1, 32, 32, 512) | weights_shape=(3, 3, 512, 512)
--relu5_2 | shape=(1, 32, 32, 512) | bias_shape=(512,)
--conv5_3 | shape=(1, 32, 32, 512) | weights_shape=(3, 3, 512, 512)
--relu5_3 | shape=(1, 32, 32, 512) | bias_shape=(512,)
--conv5_4 | shape=(1, 32, 32, 512) | weights_shape=(3, 3, 512, 512)
--relu5_4 | shape=(1, 32, 32, 512) | bias_shape=(512,)
--pool5 | shape=(1, 16, 16, 512)
VGG-19的pooling采用了长宽为2X2的max-pooling,Neural Style将它替换为了average-pooling,因为作者发现这样的效果会稍微好一些。
Neural Style
内容损失
内容损失比较好理解,将content图片p和生成的图片x,都经过VGG-19的卷积网络进行特征变换,获取某些层级输出的特征变换结果,要求二者的差异最小。二者在l层的损失函数定义如下: 
其实就是求多个中间层的特征图的L2距离。其中l代表第l层卷积的输出,i代表第i个卷积核(featur map的通道数),j代表第i个卷积核的第j个位置。
风格损失
定义风格
如何通过数学建模定义风格是实现风格迁移的关键,在网络中提取的特征图,一般来说浅层网络提取的是局部的细节纹理特征,深层网络提取的是更抽象的轮廓、大小等信息,这些特征总的结合起来表现出来的感觉就是图像的风格。风格在这篇paper中被简化为任意两种特征的相关性,相关性的描述使用余弦相似性,而余弦相似性又正比于两种特征的点积。特征向量计算出来的Gram矩阵,可以把图像特征之间隐藏的联系提取出来,也就是各个特征之间的相关性高低。如果两个图像的特征向量的Gram矩阵的差异较小,就可以认定这两个图像风格是相近的。
Gram 矩阵
Gram Matrix可看做是图像各特征之间的偏心协方差矩阵(即没有减去均值的协方差矩阵),Gram计算的是两两特征之间的相关性,哪两个特征是同时出现的,哪两个是此消彼长的等等。另一方面,Gram的对角线元素,还体现了每个特征在图像中出现的量,因此,Gram矩阵可以度量各个维度自己的特性以及各个维度之间的关系,所以可以反映整个图像的大体风格。
当我们获取了gram矩阵,实际上就是把握住了这幅作品,不同特征之间的关系与联系,比如哪一种特征的量比较多,哪些特征和出现比较多的这个特征正相关or负相关,从而得出了这个作品的风格, 而进一步通过style图片和generate图片的gram矩阵之间的计算出相应的风格损失函数,就可以比较出两者在风格之间的差异。
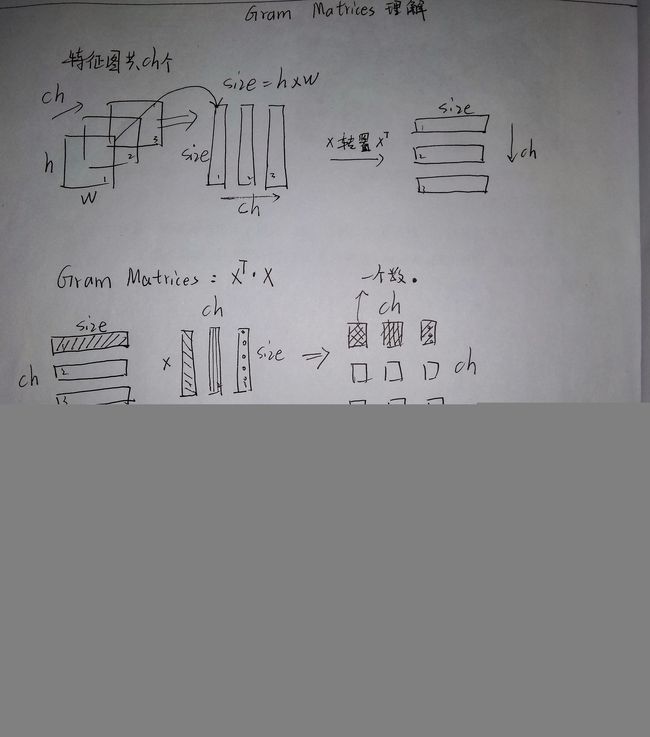
代码中通过feature map 计算Gram矩阵的过程如下:
def gram_matrix(x, area, depth):
F = tf.reshape(x, (area, depth))
G = tf.matmul(tf.transpose(F), F)
return G
关于Gram矩阵还有以下三点值得注意:
1 Gram矩阵的计算采用了累加的形式,抛弃了空间信息。一张图片的像素随机打乱之后计算得到的Gram Matrix和原图的Gram Matrix一样。所以认为Gram Matrix所以认为Gram Matrix抛弃了元素之间的空间信息。
2 Gram Matrix的结果与feature maps F 的尺寸无关,只与通道个数有关,无论H,W的大小如何,最后Gram Matrix的形状都是CXC
3 对于一个C X H X W的feature maps,可以通过调整形状和矩阵乘法运算快速计算它的Gram Matrix。即先将F调整到 C X (HW)的二维矩阵,然后再计算F 和F的转置。结果就为Gram Matrix
Gram Matrix的特点:
注重风格纹理,忽略空间信息。
计算
对于生成的图片经过第l层输出的特征向量,计算Gram矩阵:
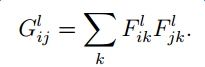
计算第l层生成图片与风格图片各自提取出的特征向量所得的Gram矩阵之间的L2损失:
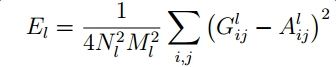
多个层之间加权求和:

总损失
将内容和风格损失结合得到总损失函数:
![]()
其中的α和β分别代表了对Content和Style的侧重,文中作者也对α/β取值的效果进行了实验。
总结
本方法的特点在于针对性,相当于训练出来的网络只用于给定的两张图,不需要额外数据集。同时导致的缺点就是对于每次风格迁移都要训练(在已经训练好的Vgg19之上进行训练,优化的变量其实就是生成图片的每个像素值,一般用内容图片地像素值作为初始化)
使用GAN训练的模型可以解决一类的风格迁移问题,但是需要大量数据集,而且没有针对性,对于某些图可能会导致输入的结构发生变化。
部分内容截自:https://segmentfault.com/a/1190000009820053
https://blog.csdn.net/weixin_40820983/article/details/85310619
推荐:https://blog.csdn.net/czp_374/article/details/81185603

