因子分析(Factor Analyse)推导以及R语言实现

因子模型

对于降维算法里，大家熟知的是SVD和PCA，甚至是t-sne。但在统计解释上来说，降维算法找到了相应的低维子空间，但解释力不足，比如PCA，对于降维后数据的解释力降低。因此对于小规模数据集，在变量众多的情况下，因子模型是较好的处理多变量的方法。通过PCA降维估计，再进行因子旋转，使得因子模型在降维的同时具备了较好的解释力。

准备工作

因子模型假设中心化的X线性依赖于一些未观测到的随机变量 F1,...,Fm F 1 , . . . , F m 和误差，称 F1,...,Fm F 1 , . . . , F m 为公共因子，因子模型可表示为以下一式：

X−μ=LF+ε X − μ = L F + ε
其中 L=(lij)p×m L = ( l i j ) p × m 为因子载荷矩阵， lij l i j 为第i个变量在第j个因子上的载荷（描述了第i个变量和第j个因子的相关性）， Fm×1 F m × 1 称为公共因子， εp×1 ε p × 1 称为特殊因子。
因子模型假设：
1. E(F)=0,Cov(F)=Im E ( F ) = 0 , C o v ( F ) = I m
2. E(ϵ)=0,Cov(ϵ)=φp×p=diag(φ1...φp) E ( ϵ ) = 0 , C o v ( ϵ ) = φ p × p = d i a g ( φ 1 . . . φ p )
3. Cov(ε,F)=0 C o v ( ε , F ) = 0
4. Cov(X)=Σp×m=LL′+φ,Cov(X,F)=Lp×m C o v ( X ) = Σ p × m = L L ′ + φ , C o v ( X , F ) = L p × m

其中第四条假设为因子模型的核心，则对于i=1,…,p,令 l(i) l ( i ) 为L的第i行，则有：

{Var(xi)=l2i1+...+l2im+φi=l′(i)l(i)+φiCov(xi,xk)=l′(i)l(k) { V a r ( x i ) = l i 1 2 + . . . + l i m 2 + φ i = l ( i ) ′ l ( i ) + φ i C o v ( x i , x k ) = l ( i ) ′ l ( k )

定义 h2i=l2i1+...+l2im=l′(i)l(i) h i 2 = l i 1 2 + . . . + l i m 2 = l ( i ) ′ l ( i ) ，即第i个变量在所有因子上的载荷平方和，称 h2i h i 2 为共性方差，共性方差反映了第i个变量对公共因子的依赖程度，也即所有因子对该变量的解释程度。

---

以上为因子模型的理论假设，省去了推导，但可以看得出来，对于p维的随机变量，因子模型假设其受一系列未被观测的公共因子控制。因子载荷矩阵反映了变量与公因子的关系，当因子数设为p时（也即和原变量维度相同），因子模型上式为等号，由谱分解， Σ=LL′ Σ = L L ′ ，这没有什么意义。因此当我们试图降维，且不损失过多信息时，也即找到m个因子（m < p）使得这m个因子能够表示大部分的信息，也即找到 Σp×m Σ p × m

PCA估计

想必大家都知道PCA主成分分析，既然是降维，则利用PCA对 Σ Σ 进行降维是个较好的方法。在此我不再讲述PCA，将直接进行推导。
根据特征值和特征向量， Σ Σ 可写成：
Σ=λ1e1e′1+...+λpepe′p=(λ1−−√e1......λp−−√ep)(λ1−−√e1......λp−−√ep)′ Σ = λ 1 e 1 e 1 ′ + . . . + λ p e p e p ′ = ( λ 1 e 1 . . . . . . λ p e p ) ( λ 1 e 1 . . . . . . λ p e p ) ′
令 L=(λ1−−√e1......λp−−√ep) L = ( λ 1 e 1 . . . . . . λ p e p ) ，此时 Σ=LL′，φ=0 Σ = L L ′ ， φ = 0
为了降维，我们取前m个主成分，即 Lp×m=(λ1−−√e1......λm−−−√em) L p × m = ( λ 1 e 1 . . . . . . λ m e m ) ，此时 φ=diag(Σ−LL′)，Σ≈LL′+φ φ = d i a g ( Σ − L L ′ ) ， Σ ≈ L L ′ + φ ，为了使得误差不要太大，因此在取前m个主成分时，要使得信息损失不要太大，这里将通过主成分的特征值来判断因子模型的方差解释力度。

第j个因子的方差解释=⎧⎩⎨⎪⎪λj^s11+...+sppλj^pviaΣ(协方差矩阵)viaR(相关系数矩阵) 第 j 个 因 子 的 方 差 解 释 = { λ j ^ s 11 + . . . + s p p v i a Σ ( 协 方 差 矩 阵 ) λ j ^ p v i a R ( 相 关 系 数 矩 阵 )

根据输入的是X的协方差矩阵或是相关系数矩阵来计算方差解释，又因为因子模型通常输入的是标准化后的变量，而标准化变量的协方差矩阵也即原变量的相关系数矩阵，因此一般采用第二个式子计算。通常模型需要85%的解释力度，因此通过观察碎石图(scree plot)以及计算累积方差可确定因子数量m。还有一个不成文的共识是选择特征值>1的的因子。
最后我们可以得到残差矩阵 E=R−(LL′+φ)或E=Σ−(LL′+φ) E = R − ( L L ′ + φ ) 或 E = Σ − ( L L ′ + φ ) 。若残差基本为0，则模型参数估计较好。
还有采用MLE极大似然估计来估计L的，但不常用，因此这里不再阐述。

因子旋转

又产生了一个新问题，我们如果目的只是降维，那么直接用PCA不就好了吗，为什么还要大费周章，设置如此多假设，最后还是采用了PCA呢？那得到的因子载荷矩阵L又有什么用呢？这里也即因子分析的核心——因子旋转。
我们知道，前期工作即找到了几个主成分，将原变量投影至特征子空间，得到了一个因子载荷矩阵的估计，那么为了更好的解释模型，解释这一系列 l(ij) l ( i j ) ，我们引入了因子旋转。
因子旋转也即对原因子做一个线性变换，使得因子解释力更强。因此，我们有两个问题，要做一个什么样的变换？变换的目的是什么？
变换有很多种，最常用的是一种叫做Varimax criterion的变换，目的是使得变换后因子载荷平方间的方差最大（这样可以使得各因子分的更开，解释力更强），从名字也可以体会出来，Varimax——Variance Max。定义

L∗^=L^T L ∗ ^ = L ^ T
其中T为该变换对应的矩阵。再定义
l∗(ij)=l(ij)^hj^ l ( i j ) ∗ = l ( i j ) ^ h j ^
l∗(ij) l ( i j ) ∗ 即旋转后的新因子，此时方差有：
V=1p∑mj=1∑pi=1(l∗(ij)2−l∗(ij)¯2)2 V = 1 p ∑ j = 1 m ∑ i = 1 p ( l ( i j ) ∗ 2 − l ( i j ) ∗ ¯ 2 ) 2
由公式 ∑pi=1(x−x¯)2=∑pi=1x2−px¯2 ∑ i = 1 p ( x − x ¯ ) 2 = ∑ i = 1 p x 2 − p x ¯ 2 可得，原式有：
V=1p∑mj=1(∑pi=1l∗(ij)4−∑pi=1(l(ij)2)2p) V = 1 p ∑ j = 1 m ( ∑ i = 1 p l ( i j ) ∗ 4 − ∑ i = 1 p ( l ( i j ) 2 ) 2 p )

因此因子旋转的目标也即使找到线性变换T，使得V–>max，即 argmaxTV a r g m a x T V .
因此经Varimax因子旋转后各个因子方差最大，我们可以对模型进行很好的解释，通过观察因子载荷矩阵，根据因子载荷值（也即各变量与各个因子的相关程度）可对各个因子进行命名，再进行后续分析。
到这里其实关于整个模型还有F尚未估计，F的估计称为因子得分，但在实际分析中主要观察的是因子载荷矩阵，因此这里不再阐述F的估计。

R语言实现

下面我先不用包，一步步实现来解释

R = matrix(c(1,.505,.569,.602,.621,.603,
             .505,1,.422,.467,.482,.45,
             .569,.422,1,.926,.877,.878,
             .602,.467,.926,1,.874,.894,
             .621,.482,.877,.874,1,.937,
             .603,.45,.878,.894,.937,1),nrow=6)
 '''
     [,1]  [,2]  [,3]  [,4]  [,5]  [,6]
[1,] 1.000 0.505 0.569 0.602 0.621 0.603
[2,] 0.505 1.000 0.422 0.467 0.482 0.450
[3,] 0.569 0.422 1.000 0.926 0.877 0.878
[4,] 0.602 0.467 0.926 1.000 0.874 0.894
[5,] 0.621 0.482 0.877 0.874 1.000 0.937
[6,] 0.603 0.450 0.878 0.894 0.937 1.000
 '''

首先建一个相关系数矩阵。再对其求特征值和特征向量，也即PCA操作

eigen_ = eigen(R)
lambda = eigen_$values 
vectors = eigen_$vectors

再输出其方差解释以及累计方差和，由于输入的是相关系数矩阵，因此直接除以p就行

p = nrow(R)
score = rep(0,p)
for(i in 1:p){
  score[i] = lambda[i]/p
}
cum.score = cumsum(score)
score
plot(score,type='b',lty=3,pch=19,main='scree plot')

输出方差解释和碎石图可得
[1] 0.7427414 0.8731431 0.9495472 0.9776860 0.9908673 1.0000000

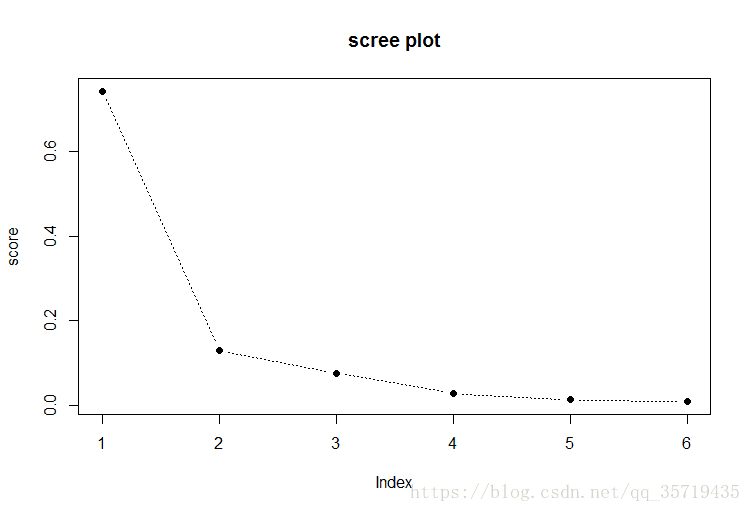
因此我们取前两个主成分，即m=2.

L_1 = sqrt(lambda[1])*vectors[,1]
L_2 = lambda[2]*vectors[,2]
L = cbind(L_1,L_2) # L = sqrt(

L即为我们的因子载荷矩阵，则我们的残差阵为

phi = diag(R-L%*%t(L))
E = R - (L%*%t(L))-phi
E

以上不包含因子模型的旋转步骤。下面将使用R语言相关库来实现。

psych

下面首先使用psych这个库，其主要用MLE来估计参数
载入数据，先进行标准化，再导入库利用fa函数

data = read.table('T9-12.DAT')
X = scale(data,center = T,scale = T) #标准化
library(psych)
m = fa.parallel(X) #确定因子数量
m$nfact
x.fa2 = fa(X,nfactors = 2,fm='mle',rotate = 'varimax')#设置了因子旋转
round(x.fa2$loadings,2)

输出因子载荷矩阵如下

Loadings:
   ML2  ML1 
V1 0.85 0.45
V2 0.87 0.42
V3 0.72 0.60
V4 0.15 0.99
V5 0.50 0.53
V6 0.62     
V7 0.95 0.28

                 ML2   ML1
SS loadings    3.557 2.082
Proportion Var 0.508 0.297
Cumulative Var 0.508 0.806

可以看到目前方差累计解释为80%。下面进行分析

fa.diagram(x.fa2)

可以看到该函数很方便的告诉我们那些变量聚为一个因子，而后我们再对两个因子分别命名即可。

principal

利用principal函数（内置），可直接进行因子分析（基于PCA），对于同一份数据集，这里我们设置因子数为3，同样设置了因子旋转为varimax

pc = principal(data,nfactors = 3,rotate='varimax')
pc$loadings

因子载荷矩阵如下

Loadings:
   RC1   RC2   RC3  
V1 0.779 0.387 0.452
V2 0.908 0.356 0.189
V3 0.616 0.548 0.483
V4 0.213 0.952      
V5 0.552 0.607 0.145
V6 0.287       0.950
V7 0.909 0.181 0.328

                 RC1   RC2   RC3
SS loadings    3.071 1.889 1.506
Proportion Var 0.439 0.270 0.215
Cumulative Var 0.439 0.709 0.924

同样的我们可以利用fa.diagram函数进行分析

fa.diagram(pc,simple=T)

利用factor.plot函数可输出因子载荷矩阵的点图

factor.plot(pc$loadings,labels = rownames(pc$loadings))