论文笔记：Graph embedding techniques, applications, and performance: A survey
一、基本信息
论文题目：《Graph embedding techniques, applications, and performance: A survey》
发表时间：
论文作者及单位：
论文地址：https://www.sciencedirect.com/science/article/pii/S0950705118301540
二、摘要
图形，例如社交网络、单词共现网络和通信网络，自然地出现在各种现实世界的应用中。分析它们可以洞察社会结构、语言和不同的交流模式。已经提出了许多方法来进行分析。最近，在向量空间中使用图节点表示的方法受到了研究界的关注。在本次调查中，我们对文献中提出的各种图形嵌入技术进行了全面和结构化的分析。我们首先介绍嵌入任务及其挑战，例如可伸缩性、维度选择、要保留的特性以及它们可能的解决方案。然后，我们提出了基于因式分解方法、随机漫步和深度学习的三类方法，每一类都有代表性算法的例子，并分析了它们在各种任务中的性能。我们在一些常见的数据集上评估这些最先进的方法，并将它们的性能相互比较。我们的分析最后提出了一些潜在的应用和未来的方向。我们最终展示了我们开发的开源Python库，名为GEM (图形嵌入方法，可在https://github.com/palash1992/GEM获得)，它在统一的界面中提供了所有展示的算法，以促进和便利对该主题的研究。
三、论文主要工作与内容
1、Introduction
由于网络在现实世界中的无处不在，近年来图分析越来越受到人们的关注。图(又名网络)已被用来表示各个领域的信息，包括生物学(蛋白质-蛋白质相互作用网络) [ 1，社会科学(友谊网络) [ 2 ]和语言学(词汇共现网络) [ 3 ]。将实体之间的相互作用建模为图形使研究人员能够以系统的方式理解各种网络系统[ 4】。例如，社交网络已被用于友谊或内容推荐等应用，以及广告[ 5】。图分析任务可以大致抽象为以下四类: ( a )节点分类[ 6 ]，( b )链接预测[ 5 ]，( c )聚类[ 7 ]，以及( d )可视化[ 8 ]。节点分类旨在基于其他标记的节点和网络拓扑来确定节点的标签(也称为顶点)。链路预测是指预测缺失链路或未来可能出现的链路的任务。聚类用于发现相似节点的子集，并将它们分组在一起；最后，可视化有助于深入了解网络结构。
在过去的几十年中，已经为上述任务提出了许多方法。对于节点分类，大致有两类方法——使用随机游走传播标签[ 9，10的方法，以及从节点提取特征并对其应用分类的方法[ 11，12 ]。链路预测的方法包括基于相似性的方法[ 13，14 ]，最大似然模型[ 15，16 ]，和概率模型[ 17，18 ]。聚类方法包括基于属性的模型[ 19 ]和直接最大化(分别。，最小化)集群间(分别。集群内)距离[ 7，20 ]。该综述将提供一个分类法，用于捕获这些应用程序域和现有策略。
通常，为解决基于图的问题而设计的模型要么在原始图邻接矩阵上运行，要么在导出的向量空间上运行。最近，基于在向量空间中表示网络的方法，在保持网络特性的同时，已经成为[ 21–23的热门方法。获得这样的嵌入在上面定义的任务中是有用的。嵌入作为特征输入到模型中，参数是基于训练数据学习的。这消除了对直接应用于图形的复杂分类模型的需要。
1.1Chanllenge
获取图中每个节点的矢量表示本质上是困难的，并且具有几个挑战，这些挑战一直在推动本领域的研究：
（i）属性选择：节点的“良好”矢量表示应保留图的结构和单个节点之间的连接。第一个挑战是选择嵌入应该保留的图形属性。考虑到图中所定义的距离度量和属性过多，这种选择可能很困难，性能可能取决于应用程序。
（ii）可扩展性：大多数真实网络都很大，包含大量节点和边缘。嵌入方法应具有可扩展性，能够处理大型图形。定义一个可扩展的模型可能具有挑战性，尤其是当该模型旨在保护网络的全局属性时。
（iii）嵌入的维数：很难找到表示的最佳维数。例如，较高的维数可能会提高重建精度，但具有较高的时间和空间复杂性。这种选择也可以是应用程序特定的，具体取决于方法：例如，如果所选模型只捕获节点之间的本地连接，那么较小的维度数量可能会导致更好的链路预测精度。
1.2 Our contribution
这项调查提供了三方面的贡献：
（1）我们提出了图嵌入方法的分类，并解释了它们的区别。我们定义了四个不同的任务，即图形嵌入技术的应用领域。我们将阐述该主题的演变、面临的挑战以及未来可能的研究方向。
（2）我们对各种图形嵌入模型进行了详细而系统的分析，并讨论了它们在各种任务中的性能。对于每种方法，我们通过对一些常见数据集和应用场景的综合比较评估，分析了保留的属性及其准确性。此外，我们对所评估的方法进行了超参数敏感性分析，以检验其鲁棒性，并提供了最优超参数对所执行任务的依赖性。
（3）为了促进这一主题的进一步研究，我们最终介绍了我们开发的开放源码python库gem，它在统一的界面下提供了本调查中讨论的所有图形嵌入方法的实现。据我们所知，这是第一篇综述图形嵌入技术及其应用的论文。
据我们所知，这是第一篇调查图形嵌入技术的论文。最近的工作回顾了当前的图形嵌入方法，并提出了类似的分类法[104105]。此外，我们的工作还侧重于图形嵌入应用程序、实现和性能。我们对多种技术进行了广泛的评估和实验比较，并对不同超参数设置的方法进行了分析。我们工作的最后一个主要区别是Python gem库的开源版本。
1.3. Organization of the survey
综述组织如下。在第2节中，我们提供了理解下一步讨论的问题和模型所需的定义。第3节提出了图嵌入方法的分类，并提供了每个类别中代表性算法的描述。第4节提供了研究人员使用图形表示学习方法的应用程序列表。然后我们描述我们的实验设置（第5节）
并评估不同的模型（第6节）。第7节介绍了我们的图形嵌入方法的python库。最后，在第8节中，我们得出了我们的结论，并讨论了潜在的应用和未来的研究方向。
2 Definitions and preliminaries
- 定义一：图，图由顶点集与边集构成，即数据结构中关于图的定义。
- 定义2（一阶近似）。边缘权重s ij也被称为节点vi和vj之间的一阶近似值，因为它们是两个节点之间第一个也是最重要的相似性度量。我们同样可以定义节点之间的高阶近似值。例如，
- 定义3（二阶近似）。一对节点之间的二阶近似性描述了该对邻域结构的邻近性。设s i=[s i 1，····，s in]表示vi和其他节点之间的一阶接近度。然后，根据si和sj的相似性确定vi和vj之间的二阶近似。二阶近似比较两个节点的邻域，如果它们具有相似的邻域，则将它们视为相似的。可以使用其他指标（如katz索引、根pagerank、公共邻居、Adamic Adar等）来定义高阶近似值（有关详细定义，请参见Ou等人，此处为空间利益省略）。〔24〕。接下来，我们定义了一个图形嵌入：
- 定义4（图形嵌入）。对于图g=（v，e），图嵌入是图的定点v i→yi∈
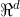i∈[n]的映射，d<
来获得接近度。让两个节点对( vi，vj )和( vi，vk )与连接强度相关联，假如Sij>Sik。在这种情况下，vi和vj将被映射到嵌入空间中比vi和vk的映射更接近的点。
3、Algorithmic approaches: a taxonomy
在过去的十年里，在图形嵌入领域已经有了大量的研究，重点是设计新的嵌入算法。最近，研究人员提出了可扩展的嵌入算法，该算法可应用于具有数百万个节点和边的图形。在下文中，我们提供了关于该领域研究进展的历史背景（第3.1节），然后提出了图嵌入技术的分类（第3.2节），包括（i）因子分解方法（第3.3节）、（i i）随机行走技术（第3.4节）、（i i i）深度学习（第3.5节）和（iv）其他方法。第3.6节）。
3.1. Graph embedding research context and evolution
20世纪初，研究人员开发了图形嵌入算法，作为降维技术的一部分。他们将基于邻域为一组n维点构建一个相似图，然后将图的节点嵌入到一个d维向量空间中，其中d<
3.2. A taxonomy of graph embedding methods
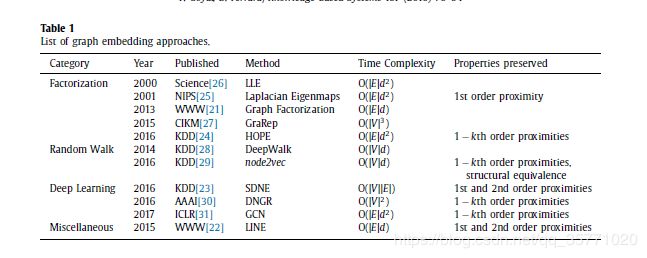
我们提出了嵌入方法的分类法。我们将嵌入方法分为三大类: ( 1 )基于因子分解的方法，( 2 )基于随机游走的方法，以及( 3 )基于深度学习的方法。下面我们解释每一个类别的特征，并使用表2中给出的符号为每一个类别提供一些代表性方法的概要(参见表1 )。
3.3. Factorization based methods
基于因式分解的算法以矩阵的形式表示节点之间的连接，并将该矩阵因式分解以获得嵌入。用于表示连接的矩阵包括节点邻接矩阵、拉普拉斯矩阵、节点转移概率矩阵和卡茨相似矩阵等。代表矩阵的因式分解方法因矩阵性质而异。如果得到的矩阵是半正定的，例如拉普拉斯矩阵，可以使用特征值分解。对于非结构化矩阵，可以使用梯度下降法来获得线性时间内的嵌入。
3.3.1. Locally Linear Embedding (LLE)
3.3.2. Laplacian Eigenmaps
3.3.3. Cauchy graph embedding
3.3.5. Graph Factorization (GF)
3.3.6. GraRep
3.3.7. HOPE
3.3.8. Additional variants
为了对高维数据进行降维，还开发了其他几种能够进行图形嵌入的方法。Yan等人[ 35 ]调查了一系列这样的方法，包括主成分分析[ 36，线性判别分析[ 37，异源映射[ 38，多维标度[ 39，局部保持性质[ 40 ]和核特征映射[ 41 ]。Matrinex等人[ 42 ] )提出了一个通用框架，非负图嵌入，它为这些算法产生非负嵌入。
许多最近的技术集中于联合学习网络结构和网络可用的附加节点属性信息。，增强关系嵌入( ARE) [43]利用图像的基于内容的特征来增强网络，并修改图-拉普拉斯算子以捕捉此类信息。文本相关深度行走( TADW) [44]对节点相似性矩阵执行矩阵分解，使用文本特征矩阵解开表示。异构网络嵌入( HNE) [45]学习网络每种模式的表示，然后使用线性变换将它们统一到一个公共空间。其他工作[ 46–48 ]在各种节点属性之间执行类似的转换，并学习联合嵌入。
3.4. Random walk based methods
随机游走已经被用来近似图中的许多属性，包括节点中心性[ 49 ]和相似性[ 50 ]。当一个人只能部分观察图形，或者图形太大而不能整体测量时，它们特别有用。已经提出了在图上使用随机行走来获得节点表示的嵌入技术: DeepWalk和node2vec是两个例子。
3.4.1. DeepWalk
3.4.2. node2vec
3.4.3. Hierarchical representation learning for networks (HARP)
3.4.4. Walklets
3.4.5. Additional variants
最近提出的上述方法有几种变化。与基于因子分解方法的节点属性图结构扩充相似，genvector[53]、鉴别性深随机游动（ddrw）[54]、三方深网络表示（tridnr）[55]和[56]扩展了随机游动，共同学习网络结构和节点属性。
3.5. Deep learning based methods
对深度学习的日益增长的研究已经导致大量基于深度神经网络的方法应用于图表[ 23，30，57 ]。由于深度自动编码器能够对数据中的非线性结构进行建模，因此它们已经被用于降维[ 58 ]。
最近，SDNE [23]，DNGR [30]利用深度自动编码器的这种能力，生成一个嵌入模型，可以捕捉图形中的非线性。
3.5.1. Structural deep network embedding (SDNE)
3.5.2. Deep neural networks for learning graph representations (DNGR)
3.5.3. Graph convolutional networks (GCN)
3.5.4. Variational graph auto-encoders (VGAE)
3.6. Other methods
3.6.1. LINE
3.7. Discussion
我们可以将嵌入解释为描述图形数据的表示。因此，嵌入可以洞察网络的属性。我们在图1中对此进行了说明。考虑一个完整的二分图。一个试图保持两个连接节点紧密(即，保持社区结构)的嵌入算法将不能捕获图的结构——如图1 (b )所示。然而，将结构等同的节点嵌入在一起的算法学习可解释的嵌入——如图1 (c )所示。同样，在1 (d )中，我们考虑一个图，其中两个星形组件通过集线器连接。节点1和3在结构上是等价的(它们链接到相同的节点)，并且在图1 (f )中聚集在一起，而在图1 (e )中它们相距很远。上面的算法可以用它们解释图的性质的能力来描述。
基于因式分解的方法不能学习任意函数，例如解释网络连通性。因此，除非明确包含在目标函数中，否则他们无法学习结构等价。在基于随机游走的方法中，等价类的混合可以通过改变随机游走参数来控制到一定程度。深度学习方法可以根据通用近似定理[ 67 ]对广泛的函数建模:给定足够的参数，它们可以学习社区和结构等价的混合，以嵌入节点，从而最小化重构误差。我们可以将自动编码器的权重解释为图形结构的表示。例如，图1 (c )为完全二部图G 1绘制了由SDNE学习的嵌入。自动编码器将二分结构存储在权重中，实现了完美的重构。鉴于现实世界图的各种性质，使用跨越一大类函数的一般非线性模型是一个值得进一步探索的有希望的方向。
4. Applications
图形表示、嵌入可以用于多种任务。这些应用可大致分为:网络压缩(第4.1节)、可视化(第4.2节)、集群(第4.3节)、链路预测(第4.4节)和节点分类(第4.5节)。
4.1. Network compression
4.2. Visualization
4.3. Clustering
4.4. Link prediction
4.5. Node classification
5. Experimental setup
我们的实验评估了在之前的四个应用领域中使用上述方法获得的特征表示。接下来，我们指定我们使用的数据集和评估指标。实验在Ubuntu 14.04.4 LTS系统上进行，该系统具有32个内核、128千兆位随机存取存储器和2.6千兆赫的时钟速度。用于基于深层网络模型的图形处理器是英伟达特斯拉K40C。
5.1. Datasets
5.2. Evaluation metrics
6. Experiments and analysis
.
6.6. Discussion
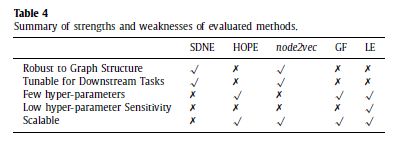
我们总结了表4中评估方法的优缺点。
在我们的实验中，我们观察到SDNE在所有下游任务的大多数数据集上都表现良好。由于SDNE没有对图形结构进行假设，并且使用图形中提供的信息来学习合适的自动编码器，因此它几乎可以针对任何图形和任务进行调优。此外，对于不同的下游任务，可以单独设置超参数，以便更好地执行任务。然而，SDNE有许多超参数，性能很大程度上取决于它们的设置。大量的参数使得它不适合于大型图形。
我们还观察到，node2vec在大多数任务上都表现良好，在节点分类中表现最佳。可以为手头的任务设置随机行走偏差权重值。该方法在节点数和嵌入尺寸上是线性的，因此具有可扩展性。此外，它可以通过在不同的机器上执行随机行走在集群上并行化。
Hope和GF几乎没有需要调整的超参数，但是模型的性能在很大程度上取决于图形结构。虽然正则化参数可以作为图重构和链路预测之间的折衷，但是这些方法并不能捕获结构等效性，这对于节点分类和可视化至关重要。
拉普拉斯特征映射是一种无参数的方法，可以快速评估任务的性能。但是，其性能无法与其他方法相比，也无法针对任务进行调整。
四、总结
图嵌入技术的综述涵盖了三大类方法：基于因子分解、基于随机游走和基于深度学习。我们研究了各种嵌入方法所保留的结构和特性，并描述了一般情况下图嵌入技术以及各种方法所面临的挑战。我们报告了嵌入的各种应用程序及其各自的评估指标。我们使用几个公开的真实网络对这些应用程序的调查方法进行了经验评估，并比较了它们的优缺点。最后，我们提出了一个开源的python库，名为gem，我们开发了嵌入方法，包括图形重建、链接预测、节点分类和可视化。
我们认为，在图形嵌入领域有三个有前途的研究方向：（1）探索非线性模型；（2）研究网络演化；（3）生成具有现实世界特征的合成网络作品。如调查所示，一般非线性模型（如基于深度学习的模型）在捕获图形的固有动力学方面显示出巨大的潜力。它们能够对任意函数进行近似处理，从而最好地解释网络的边缘，这可能导致网络的高度压缩表示。这种方法的一个缺点是解释能力有限。进一步的研究集中在解释这些模型所学的嵌入方面会非常有成效。利用嵌入技术研究图形演化是一个需要进一步探索的新领域。Dai等人最近的研究。[97]，Goyal等人[98]和Zhu等人[99]继续这一思路，并说明如何将嵌入用于动态图。用真实世界的特性生成合成网络已经成为一个热门的研究领域[100]，主要是为了便于模拟。实图的低维矢量表示有助于理解其结构，从而有助于生成具有真实世界特征的合成图。学习嵌入生成模型可以在这方面帮助我们。