量化金融分析AQF（11）：配对交易Pair trading 基础

 

目录

1. 数据准备 & 回测准备

2. 策略开发思路

3. 计算策略年化收益并可视化

4.策略问题

---

 

         配对交易(Pairs Trading)起源于八十年代中期，是经典的统计套利策略之一。配对交易在《Pairs Trading: Quantitative Methods and Analysis》一书中，通常所说的配对交易：基于统计套利的配对交易，即寻找两只股价具备均衡关系的股票进行配对，如果它们的价格走势偏离历史均值，做多股价较低的股票，做空近期相对的强势股，并期待它们的股价回归到长期均衡关系。

一个平稳序列是指数据的期望不会随时间改变，数据的方差与协方差不会随时间而改变，并且固定一个时间，往前与往后进行回归都是相同的。所以平稳的股票是有很多统计上的好性质，可以进行套利操作，当股价达到一定高度时就要卖出，当股价低于一定数值时就需要买入，也就是俗称的低买高卖。但是一般在现实生活中不存在平稳的股票，所以很难去预测他在什么地方是高点什么地方是低点，这也就解释了为什么这么多人都是买高卖低了。

1、平稳的股票：

2只股票最好是具有平稳性，但是这是一个很高的要求，基本上大部分股票都不太满足。

大部分股票都是不平稳的，均值方差都会发生一定的改变。

2、不平稳的股票：

两种方法：

• 拆分，如：一阶差分
• 协整关系，具体解释

 

这篇博客使用2个在一段时间内相对平稳性股票做配对交易，下篇博客具体探讨使用协整关系的配对交易。

这篇博客是配对交易的基础，不太符合经济学的假设，但是可以很好理解配对交易，可以说明一些问题。

 

GitHub完整代码下载：https://github.com/455125158/CSDN-AQF

 

import pandas as pd
import numpy as np
import tushare as ts
import seaborn
%matplotlib inline
from matplotlib import pyplot as plt
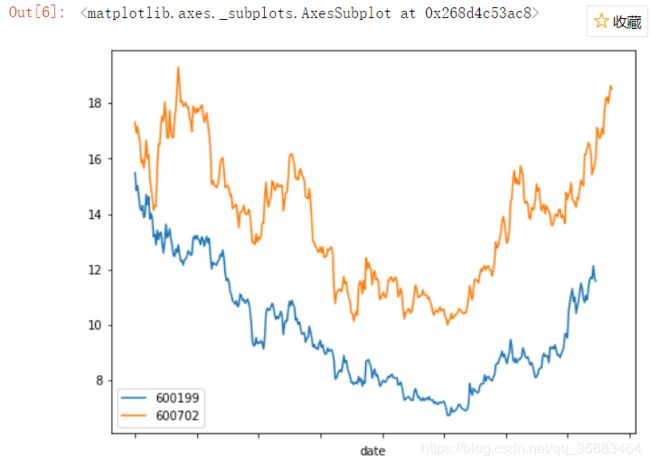
stocks_pair = ['600199', '600702']

 

1. 数据准备 & 回测准备

data1 = ts.get_k_data('600199', '2013-06-01', '2014-12-31')[['date','close']]
data2 = ts.get_k_data('600702', '2013-06-01', '2014-12-31')['close']
data = pd.concat([data1, data2], axis=1)                 #拼接，把两张表格的数据拼接起来；

data.set_index('date',inplace = True)
data.columns = stocks_pair

data.plot(figsize= (8,6))

 

2. 策略开发思路

首先进行：价差标准化=（价差-价差均值）/价差的标准差，可以近似把标准化后的价差看做满足正态分布（但是不一定满足，股票价格服从对数正太分布，股票的return符合正太分布，价格就不一定符合正太分布，这就是之前说的不严谨的地方，但是可以说明配对交易的核心，下篇博客会解决这个问题）

整体思路是，超过1.5倍价差标准化，就做多一个做空一个；低于1.5倍价差标准化，就反过来

差价：

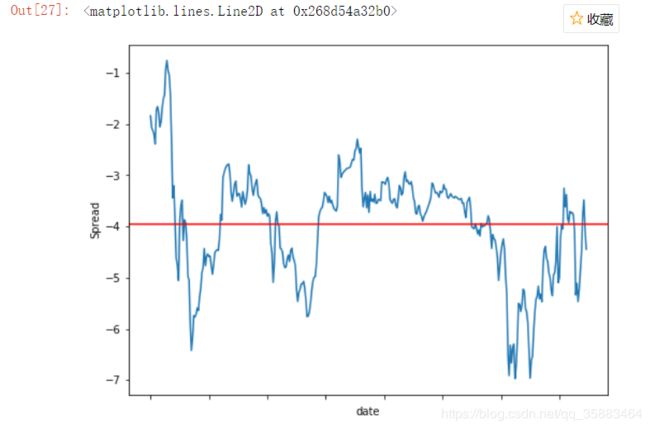
data['priceDelta']=data['600199']-data['600702']
data['priceDelta'].plot(figsize= (8,6))
plt.ylabel('Spread')
plt.axhline(data['priceDelta'].mean(), color='r')

标准化：

data['zscore'] = (data['priceDelta'] - np.mean(data['priceDelta']))/np.std(data['priceDelta'])     #价差的标准化；

策略：

data['position_1'] = np.where(data['zscore'] > 1.5, -1, np.nan)
data['position_1'] = np.where(data['zscore'] < -1.5, 1, data['position_1'])
data['position_1'] = np.where(abs(data['zscore']) < 0.5, 0, data['position_1'])

产生交易信号：

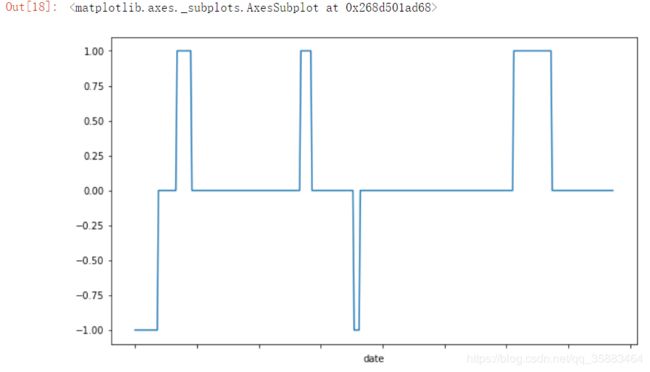
data['position_1'] = data['position_1'].fillna(method = 'ffill')
data['position_1'].plot(ylim=[-1.1, 1.1], figsize=(10, 6))
data['position_2'] = -np.sign(data['position_1'])
data['position_2'].plot(ylim=[-1.1, 1.1], figsize=(10, 6))

 

3. 计算策略年化收益并可视化

data['returns_1'] = np.log(data['600199'] / data['600199'].shift(1))
data['returns_2'] = np.log(data['600702'] / data['600702'].shift(1))
data['strategy'] = 0.5*(data['position_1'].shift(1) * data['returns_1'])+0.5*
                   (data['position_2'].shift(1) * data['returns_2'])      #等权比重
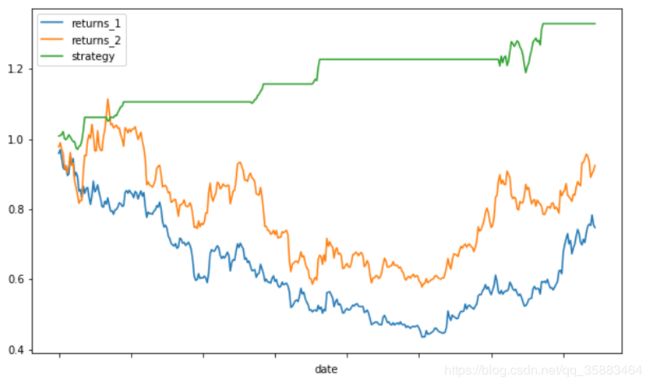
data[['returns_1','returns_2','strategy']].dropna().cumsum().apply(np.exp).plot(figsize=(10, 6))

 

4.策略问题

 

1.只股票没有做任何的处理，没有分析平稳性，直接算差价。

2.价差不一定服从正态分布。

3.并且使用的了未来函数，在实盘中并不知道这一年的价差实多少，应该价差是要随着时间推移而更新，而不是一次性算出来。

下篇博客，我会从时间序列平稳性的角度，解决以上问题。