Adaboost 算法介绍(针对算法面试)
Adaboost 算法介绍
1. Adaboost简介
1.1 集成学习(ensemble learning)背景介绍
集成学习(ensemble learning)通过构建并结合多个学习器(learner)来完成学习任务,通常可获得比单一学习器更良好的泛化性能(特别是在集成弱学习器(weak learner)时)。
目前集成学习主要分为2大类:
一类是以bagging、Random Forest等算法为代表的,各个学习器之间相互独立、可同时生成的并行化方法;
一类是以boosting、Adaboost等算法为代表的,个体学习器是串行序列化生成的、具有依赖关系,它试图不断增强单个学习器的学习能力。
1.2 Adaboost背景介绍
Adaboost是Yoav Freund和Robert Schapire在1997年提出的一种集成学习(ensemble learning)算法。
此前也Schapire也曾提出了一种boosting算法(Schapire’s Boosting ),但实际应用效果并不好,主要原因是因为Schapire’s Boosting 对于训练集样本的选取条件十分精确而又苛刻,以至于很难找出符合条件的训练集。而Adaboost在选取样本的时候采用了基于概率分布(也可解释为基于权值)来选取样本的方法,相比Schapire’s Boosting 放宽了对于训练样本选取的要求。
2. Adaboost 算法详解
2.1 Adaboost 步骤概览
① 初始化训练样本的权值分布,每个训练样本的权值应该相等(如果一共有N个样本,则每个样本的权值为1/N)
② 依次构造训练集并训练弱分类器。如果一个样本被准确分类,那么它的权值在下一个训练集中就会降低;相反,如果它被分类错误,那么它在下个训练集中的权值就会提高。权值更新过后的训练集会用于训练下一个分类器。
③ 将训练好的弱分类器集成为一个强分类器,误差率小的弱分类器会在最终的强分类器里占据更大的权重,否则较小。
2.2 Adaboost 算法流程
给定一个样本数量为m的数据集T=
{ ( x 1 , y 1 ) , … , ( x m , y m ) } \left \{\left(x_{1}, y_{1}\right), \ldots,\left(x_{m}, y_{m}\right) \right \} {(x1,y1),…,(xm,ym)}
yi 属于标记集合{-1,+1}。
训练集的在第k个弱学习器的输出权重为
D ( k ) = ( w k 1 , w k 2 , … w k m ) ; w 1 i = 1 m ; i = 1 , 2 … m D(k)=\left(w_{k 1}, w_{k 2}, \ldots w_{k m}\right) ; \quad w_{1 i}=\frac{1}{m} ; i=1,2 \ldots m D(k)=(wk1,wk2,…wkm);w1i=m1;i=1,2…m
① 初始化训练样本的权值分布,每个训练样本的权值相同:
D ( 1 ) = ( w 11 , w 12 , … w 1 m ) ; w 1 i = 1 m ; i = 1 , 2 … m D(1)=\left(w_{1 1}, w_{1 2}, \ldots w_{1 m}\right) ; \quad w_{1 i}=\frac{1}{m} ; i=1,2 \ldots m D(1)=(w11,w12,…w1m);w1i=m1;i=1,2…m
② 进行多轮迭代,产生T个弱分类器。
for t = 1, … , T :
a. 使用权值分布 D(t) 的训练集进行训练,得到一个弱分类器
G t ( x ) : χ → { − 1 , + 1 } G_{t}(x) : \quad \chi \rightarrow\{-1,+1\} Gt(x):χ→{−1,+1}
b. 计算 Gt(x) 在训练数据集上的分类误差率(其实就是被 Gt(x) 误分类样本的权值之和):
e t = P ( G t ( x i ) ≠ y i ) = ∑ i = 1 m w t i I ( G t ( x i ) ≠ y i ) e_{t}=P\left(G_{t}\left(x_{i}\right) \neq y_{i}\right)=\sum_{i=1}^{m} w_{t i} I\left(G_{t}\left(x_{i}\right) \neq y_{i}\right) et=P(Gt(xi)̸=yi)=i=1∑mwtiI(Gt(xi)̸=yi)
c. 计算弱分类器 Gt(x) 在最终分类器中的系数(即所占权重)
α t = 1 2 ln 1 − e t e t \alpha_{t}=\frac{1}{2} \ln \frac{1-e_{t}}{e_{t}} αt=21lnet1−et
d. 更新训练数据集的权值分布,用于下一轮(t+1)迭代
D ( t + 1 ) = ( w t + 1 , 1 , w t + 1 , 2 , ⋯ w t + 1 , i ⋯ , w t + 1 , m ) D(t+1)=\left(w_{t+1,1} ,w_{t+1,2} ,\cdots w_{t+1, i} \cdots, w_{t+1, m}\right) D(t+1)=(wt+1,1,wt+1,2,⋯wt+1,i⋯,wt+1,m)
for i = 1, … , m:
w t + 1 , i = w t , i Z t × { e − α t ( i f G t ( x i ) = y i ) e α t ( i f G t ( x i ) ≠ y i ) = w t , i Z t exp ( − α t y i G t ( x i ) ) w_{t+1,i}=\frac{w_{t,i}}{Z_{t}} \times \left\{\begin{array}{ll}{e^{-\alpha_{t}}} & {\text ({ if } G_{t}\left(x_{i}\right)=y_{i}}) \\ {e^{\alpha_{t}}} & {\text ({ if } G_{t}\left(x_{i}\right) \neq y_{i}})\end{array}\right. = \frac{w_{t,i}}{Z_{t}} \exp \left(-\alpha_{t} y_{i} G_{t}\left(x_{i}\right)\right) wt+1,i=Ztwt,i×{e−αteαt(ifGt(xi)=yi)(ifGt(xi)̸=yi)=Ztwt,iexp(−αtyiGt(xi))
其中 Zt是规范化因子,使得D(t+1)成为一个概率分布(和为1):
Z t = ∑ j = 1 m w t , i exp ( − α t y i G t ( x i ) ) Z_{t}=\sum_{j=1}^{m} w_{t,i} \exp \left(-\alpha_{t} y_{i} G_{t}\left(x_{i}\right)\right) Zt=j=1∑mwt,iexp(−αtyiGt(xi))
③ 集成T个弱分类器为1个最终的强分类器:
G ( x ) = sign ( ∑ t = 1 T α t G t ( x ) ) G(x)=\operatorname{sign}\left(\sum_{t=1}^{T} \alpha_{t} G_{t}(x)\right) G(x)=sign(t=1∑TαtGt(x))
2.3 权值更新过程举例说明
用一个例子阐释上面所说的权值更新过程:
给定一个数据集T,由10个训练样本组成:x1,x2 ,…,x10,整个训练集样本总数 m=10。初始权重设置为
w 1 i = 1 m = 0.1 \quad w_{1 i}=\frac{1}{m}=0.1 w1i=m1=0.1
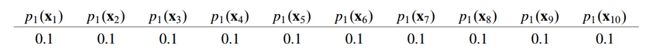
根据权值分布,我们训练出第一个弱分类器G1(对于无法接受带权样本的基学习算法,可以通过重采样resampling来处理,后面会举例介绍一下)。假设分类器G1在数据集T上的效果为:正确分类出样本 x1 - x7,将样本 x8 - x10 错误分类。我们可以计算出赋权后的误差率:
e 1 = ∑ i = 1 10 w 1 i I ( G 1 ( x i ) ≠ y i ) = 0.3 e_{1}=\sum_{i=1}^{10} w_{1 i} I\left(G_{1}\left(x_{i}\right) \neq y_{i}\right)=0.3 e1=i=1∑10w1iI(G1(xi)̸=yi)=0.3
可以求出系数 α1 = 0.424,
根据上面 ②-d 步骤我们可以得出新的权值(还未规范化):
经过规范化因子规范化后的权值分布(和为1):
下一个分类器从此分布中产生。
3. 注意要点
(1)分类器的权重系数 α 实际上是通过最小化指数损失函数的得到的,如果想了解 α 的 推导过程可以参考 Schapire 论文原文或者周志华《机器学习》8.2节内容。
(2)对于无法接受带权样本的基学习算法,可以通过重采样resampling来产生训练集,这也是为什么之前说Adaboost可以理解为基于概率分布来选取样本。拿上面的例子来说,详细做法是:10个样本中每个样本被抽中的概率是Pi(i=1,…,10),现在按抽取概率连续做10次可放回的样本抽取,得到训练集即可训练出一个分类器。
(3)adaboost的灵魂在于其样本权重更新(样本权重模拟了概率分布)的方法 以及 弱分类器加权组合。
4. 相关面试题
(1)简述一下 Adaboost 的权值更新方法。
答:参考上面的算法介绍。
(2)训练过程中,每轮训练一直存在分类错误的问题,整个Adaboost却能快速收敛,为何?
答:每轮训练结束后,AdaBoost 会对样本的权重进行调整,调整的结果是越到后面被错误分类的样本权重会越高。而后面的分类器为了达到较低的带权分类误差,会把样本权重高的样本分类正确。这样造成的结果是,虽然每个弱分类器可能都有分错的样本,然而整个 AdaBoost 却能保证对每个样本进行正确分类,从而实现快速收敛。
(3) Adaboost 的优缺点?
答:优点:能够基于泛化性能相当弱的的学习器构建出很强的集成,不容易发生过拟合。
缺点:对异常样本比较敏感,异常样本在迭代过程中会获得较高的权值,影响最终学习器的性能表现。
(4)AdaBoost 与 GBDT 对比有什么不同?
答:区别在于两者boosting的策略:Adaboost通过不断修改权重、不断加入弱分类器进行boosting;GBDT通过不断在负梯度方向上加入新的树进行boosting。
参考资料:
-
台湾清华大学李端兴教授2017年秋机器学习概论课程(CS 4602)PPT
-
周志华 《机器学习》第8章 集成学习
-
July的博客