【李宏毅深度强化学习2018】P1 Policy Gradient(Review)
第一讲 Policy Gradient (Review)
PPO是 Policy Gradient 的变形,下面先复习 Policy Gradient。
视频地址:https://www.bilibili.com/video/av24724071
课件地址:http://speech.ee.ntu.edu.tw/~tlkagk/courses_MLDS18.html
第二讲整理:【李宏毅深度强化学习2018】P2 Proximal Policy Optimization (PPO)
第三讲整理:【李宏毅深度强化学习2018】P3 Q-learning(Basic Idea)
policy gradient的基本组成:
Policy Gradient中的 Basic Components 有三个:actor、environment、reward function。其中env和reward function是你不能控制的,你只能控制actor。
Policy of Actor:
actor 的 policy 决定了 actor 的行为,policy ![]() 是一个由参数
是一个由参数 ![]() 表示的网络。网络的输入是 machine 的所见(observation),用vector 或 matrix 表示。网络的输出是 machine 采取的行为。比如上图左边的当前游戏画面就是输入,经过网络后对于三种可能的输出行为(左移、右移、开火)分别得到三个分数,作为分别采取这三种行为的概率。
表示的网络。网络的输入是 machine 的所见(observation),用vector 或 matrix 表示。网络的输出是 machine 采取的行为。比如上图左边的当前游戏画面就是输入,经过网络后对于三种可能的输出行为(左移、右移、开火)分别得到三个分数,作为分别采取这三种行为的概率。
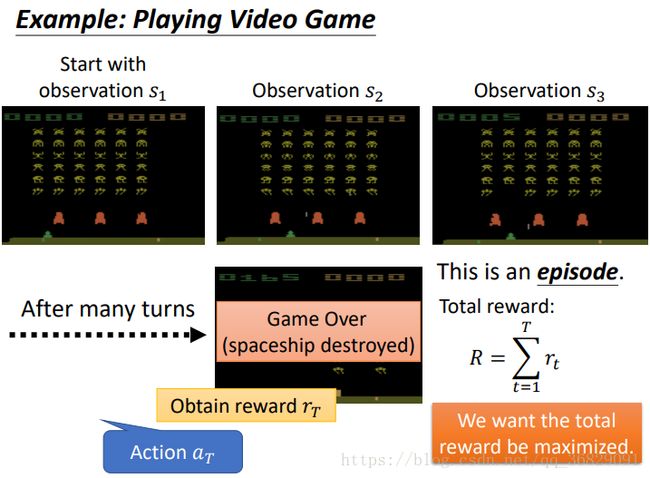
一个例子:
初始的游戏画面作为 ![]() ,针对
,针对 ![]() 采取的动作为
采取的动作为 ![]() ,行动后悔得到一个reward记为
,行动后悔得到一个reward记为 ![]() 。之后会看到下一个游戏画面
。之后会看到下一个游戏画面 ![]() ...
...
经过很多轮 ![]() 后游戏结束了,从开始到结束玩的这一次游戏称为一个episode,将每一轮的 reward 相加就能得到Total reward:
后游戏结束了,从开始到结束玩的这一次游戏称为一个episode,将每一轮的 reward 相加就能得到Total reward: 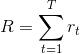 。actor 的目标就是将 Total reward R 最大化。
。actor 的目标就是将 Total reward R 最大化。
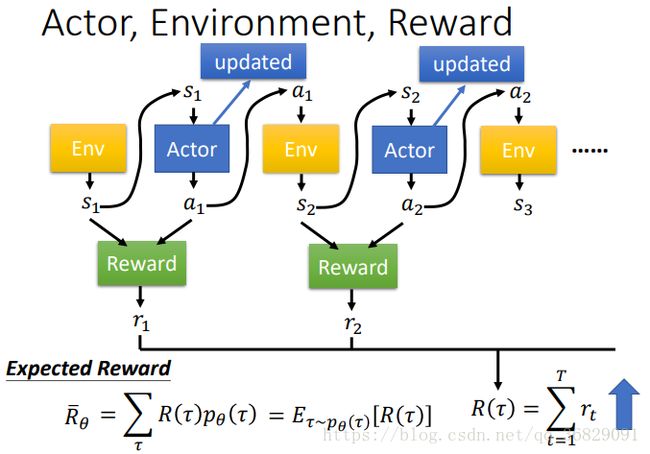
Actor, Environment, Reward:
我们可以将 environment 和 actor 都看做一个网络,action 经过 env 会得到新的 state ,state 经过 actor 会得到新的 action。将 ![]() 的序列称为 trajectory
的序列称为 trajectory ![]() 。在给定网络参数
。在给定网络参数 ![]() 的情况下,可以计算每一个
的情况下,可以计算每一个 ![]() 存在的概率
存在的概率 ![]() 。即产生
。即产生 ![]() 的概率 * 给定
的概率 * 给定 ![]() 情况下采取
情况下采取 ![]() 的概率 * 在出现
的概率 * 在出现 ![]() 情况下产生
情况下产生 ![]() 的概率···
的概率···
其中 ![]() 取决于游戏主机。即
取决于游戏主机。即 ![]() 由环境决定,我们无法控制,而
由环境决定,我们无法控制,而 ![]() 由actor控制。采取不同的
由actor控制。采取不同的 ![]() ,就会得到不同的 trajectory。
,就会得到不同的 trajectory。
给定一个 ![]() 可以得到一局游戏的 R,我们现在要做的就是调整actor中的参数,使得
可以得到一局游戏的 R,我们现在要做的就是调整actor中的参数,使得 ![]() 最大化。注意
最大化。注意 ![]() 不是常量 scalable,而是随机变量 random variable,因为采取哪个action是有随机性的,而环境给出哪个state也是有随机性的。
不是常量 scalable,而是随机变量 random variable,因为采取哪个action是有随机性的,而环境给出哪个state也是有随机性的。
所以对于 R 我们要算它的期望 ![]() ,算法是穷举所有的trajectory
,算法是穷举所有的trajectory ![]() 并计算每个
并计算每个 ![]() 出现的概率,最后算
出现的概率,最后算 ![]() 。或者这样理解:从
。或者这样理解:从 ![]() 的分布中采样(sample)出一个
的分布中采样(sample)出一个 ![]() ,然后计算
,然后计算 ![]() 的期望。
的期望。
Policy Gradient:
为了使 ![]() 最大化,我们需要做gradient ascent(不是gradient descent!),即对
最大化,我们需要做gradient ascent(不是gradient descent!),即对 ![]() 求梯度。注意
求梯度。注意 ![]() 中
中 ![]() 是不可微的,但不影响。
是不可微的,但不影响。
![]() 是无法计算的,所以sample出N个
是无法计算的,所以sample出N个 ![]() ,对每个
,对每个 ![]() 求
求 ![]() 再求和。
再求和。
上面提到 ![]() 由环境决定,我们无法知道也无法计算梯度,只能算
由环境决定,我们无法知道也无法计算梯度,只能算 ![]() 的梯度,所以最后
的梯度,所以最后 ![]() 改写为
改写为 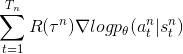 。
。
理解一下最后的 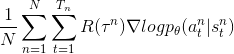 :若在
:若在 ![]() 下执行
下执行 ![]() 使得
使得 ![]() 为正,则增加概率
为正,则增加概率 ![]() ;为负则减少概率。
;为负则减少概率。
左边的方框是做sample,获得很多 (s, a) 的pair(代表在s下采取a,得到 ![]() )。然后将这些数据送入训练过程中计算
)。然后将这些数据送入训练过程中计算 ![]() 。然后更新模型。注意数据只用一次。
。然后更新模型。注意数据只用一次。
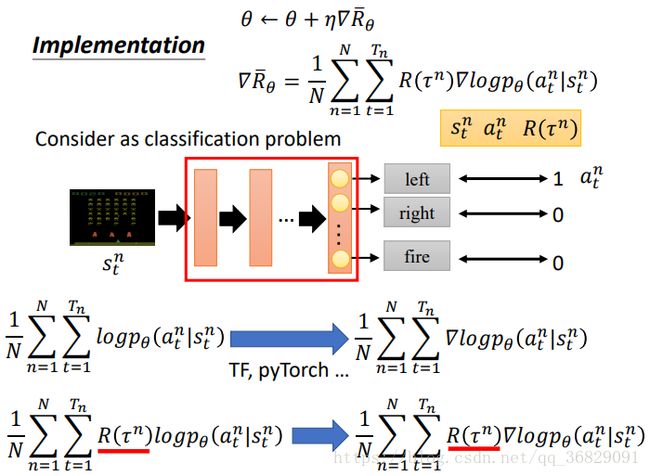
反向梯度的计算和使用方法:
训练 actor 的过程类似于分类,分类的输入就是 state(在sample过程中获得),输出的不同的 action 视为不同的类别。
上图下面的两个公式,分别代表分类问题的反向梯度和强化学习 policy gradient 的反向梯度。
最小化 loss-entropy 就是最大化 ![]() 。与一般的分类问题不同的是,RL要乘上一个权重
。与一般的分类问题不同的是,RL要乘上一个权重 ![]() ,注意这是整个游戏的 R,不是每个动作后得到的reward。
,注意这是整个游戏的 R,不是每个动作后得到的reward。
以下是policy gradient的两个小技巧:
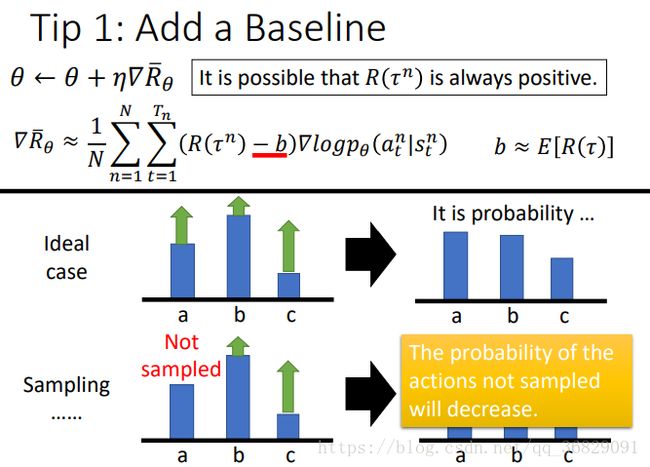
技巧1:add a baseline
之前约定的做法:假如执行 action a 后 R 为正,则提高 action a 出现的概率;R 为负,则降低 action a 出现的概率。
但是可能某个游戏不管什么执行动作得到的 reward 都是正的(比如0-20),则若执行 action a 后 R 小,则 action a 出现概率增加得少;执行 action b 后R大,则 action b 出现概率增加得多。(注意在reward恒为正的情况下,看起来无论如何执行某 action 的概率都会增加,只是增加多少的问题)但因为所有action出现的概率和为1,那么在归一化后相当于 action a 出现概率下降而 action b 出现概率增加。(即增加得少的归一化后相当于下降,增加得多的归一化后才上升)
问题是在sample中可能有些动作没有sample到,比如 action a(我们不知道这个action得到的reward是大是小),但归一化后 action a 出现的概率会必然下降(因为 action b/c 出现的概率无论如何都会上升,这样就把 action a 出现的概率给压下去了),这显然是不妥的。
为了解决这个问题,我们希望reward不要总是正的,所以 ![]() ,b是一个baseline,这样如果一个 reward 是一个很小的正值,减掉b后就会变负。
,b是一个baseline,这样如果一个 reward 是一个很小的正值,减掉b后就会变负。![]() 可以用
可以用 ![]() 的平均值代替。
的平均值代替。
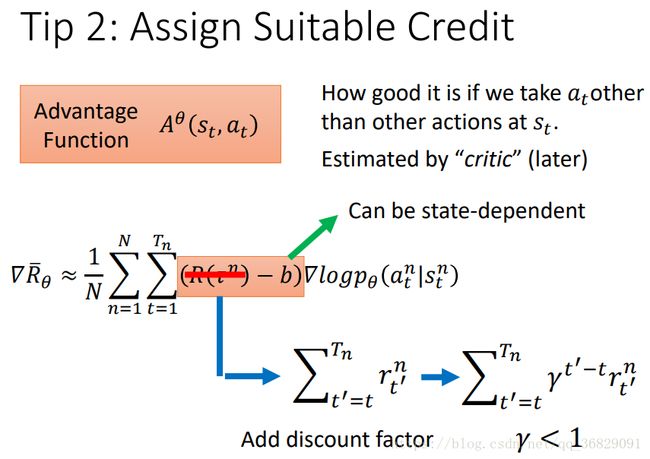
技巧2:assign suitable credit
由上图可知,在同一场游戏中,不管其中的某个 action 是好是坏,总会乘上相同的权重 R,这显然也是不公平的。比如上图左边部分,整场游戏的 reward 是+3,按规定其中三个 ![]() 都要被乘上 3 的权重,但是
都要被乘上 3 的权重,但是 ![]() 未必见得好,因为执行
未必见得好,因为执行 ![]() 后的即时得分是 -2。如果我们sample的次数够多,可能会看出
后的即时得分是 -2。如果我们sample的次数够多,可能会看出 ![]() 不够好,这个问题能够得到解决。但是在sample次数不够多的情况下,我们希望每个action的权重不同。
不够好,这个问题能够得到解决。但是在sample次数不够多的情况下,我们希望每个action的权重不同。
解决的方法是,不把整场游戏的 R(+5+0+-2=+3)作为统一权重,而将执行该动作后剩下序列的【reward之和】作为该动作的权重。比如对于 ![]() ,它的权重应该为(+0-2=-2)。即执行某个 action 前得到多少 reward 都跟该 action 无关,该 action 只影响之后的游戏过程。
,它的权重应该为(+0-2=-2)。即执行某个 action 前得到多少 reward 都跟该 action 无关,该 action 只影响之后的游戏过程。
所以把权重中的 ![]() 换成
换成 ![]() ,其中 t 代表该 action 执行的时刻,
,其中 t 代表该 action 执行的时刻,![]() 代表游戏结束的时刻,即把当前的 r 以及之后每一步的 r 做一个求和。
代表游戏结束的时刻,即把当前的 r 以及之后每一步的 r 做一个求和。
还需要考虑的一点是,当前的 action 对之后游戏的影响会随之时间推移而减弱,所以我们要有 discount,在求和的每一步都乘上一个小于1的 ![]() (比如0.9),这样 action 之后的动作越多,即时分数乘上的
(比如0.9),这样 action 之后的动作越多,即时分数乘上的 ![]() 越多。
越多。
把 ![]() 这一项称作
这一项称作 ,它依赖于
,它依赖于 ![]() ,上标
,上标 ![]() 代表
代表 ![]() 对应的 actor 对 state 所作出的 action。advantage function代表的是对于某个
对应的 actor 对 state 所作出的 action。advantage function代表的是对于某个 ![]() 相较于其它action(同样对于
相较于其它action(同样对于![]() )有多好。
)有多好。