A-Star（A*）算法

【由于专栏后几篇限制vip观看，我又把完整算法在公众号“武汉AI算法研习”进行了发布，可以查看全专栏文章。】

A-Star(A*)算法作为Dijkstra算法的扩展，在寻路和图的遍历过程中具有一定的高效性。

【适用范围】静态图搜索

【算法流程】A-Star算法中采用的估价函数如下,其中*h(i)的引入可以防止搜索过程中过渡跑偏到很多非常遥远的路径，但是这个h(i)*是未知的，计算中采用一个可以估计的值进行表达，一般用简单的曼哈顿距离
$$\begin{gathered} f(i)=g(i)+h(i)； \\ 当前节点的价值估值f(i)=起始点到该节点的距离g(i)+当前节点距离终点的距离h(i)(启发函数) \end{gathered}$$
【搜索开始】如图方形格，绿色表示起点，红色表终点，其中蓝色为障碍物。路径必须以绿色格为起点绕过蓝色障碍物抵达红色格子。现有格子水平方向移动一格开销为10，沿对角线移动一格开销等于14。我们将路径规划过程中待检测的节点存放于Open List中，而已检测过的格子则存放于Close List中。

【第一步：以起点开始搜索周围8个格子】起点周围8个点是可能会经过的，所以把他们加入Open list中，同时指定其父节点为起始节点(32)。以起点格子右边方格为例，其距离起点距离为G=10，启发函数值采用曼哈顿距离则H=30，则价值函数F=G+H=40，以此类推得到其周围8个格子的价值函数，选取最小价值函数(33号节点)作为下一个目标。
$$\begin{gathered} Openlist=21(父节点=32,f值=74), \\ 22(父节点=32,f值=60),23(父节点=32,f值=54), \\ 31(父节点=32,f值=60),33(父节点=32,f值=40), \\ 41(父节点=32,f值=74),42(父节点=32,f值=60),43(父节点=32,f值=54) \\ Clostlist=32 \end{gathered}$$

【第二步：以33号节点】对33号节点周围的8个节点进行判断，若是不可通过或是已经存在Clost list节点则忽略不考虑，若当前处理节点的相邻格子已经在Open List中，则检查这条路径是否更优，即计算经由当前处理节点到达那个方格是否具有更小的 G值。如果没有，不做任何操作。相反，如果G值更小，则把那个方格的父节点设为当前处理节点 ( 我们选中的方格 ) ，然后重新计算那个方格的 F 值和 G 值。

33号节点此时需要检查的点为23号、22号、42号和43号节点。23号节点目前G值14，如果经33号抵达则G值为20，因此不做更新；22号节点也无需更新，42号节点也无需更新，43号节点也无需更新。因此遍历Open list节点取f值最小的为43号节点，则加入Clost list中
$$\begin{gathered} Openlist=21(父节点=32,f值=74),22(父节点=32,f值=60),23(父节点=32,f值=54), \\ 31(父节点=32,f值=60), \\ 41(父节点=32,f值=74),42(父节点=32,f值=60),43(父节点=32,f值=54) \\ Clostlist=32，33 \end{gathered}$$

【第三步：以43号节点】以43号节点为中心，加入其周边可选节点并计算相应的G值和H值。则选择其中价值最小的节点为42号节点。
$$\begin{gathered} Openlist=21(父节点=32,f值=74),22(父节点=32,f值=60),23(父节点=32,f值=54), \\ 31(父节点=32,f值=60), \\ 41(父节点=32,f值=74),42(父节点=32,f值=60) \\ 52(父节点=43,f值=88),53(父节点=43,f值=74) \\ Clostlist=32，33，43 \end{gathered}$$

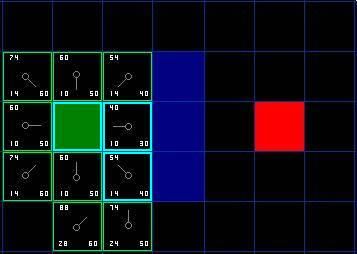
【不断重复以上操作，直到把终点加入到Open list中】最终沿着父节点从终点开始回溯到起点即时最短距离路径。

总结：A-Star最短路径距离算法通过引入启发式函数，每一步计算抵达起点和终点的估计距离从而可以更快、更省的得到最短路径，但是A-Star算法一般只能用于静态图中，对于动态图没次图形变换都需要用A-Star进行计算，计算开销很大。