机器学习之朴素贝叶斯分类方法

本文转载自http://holynull.leanote.com/post/Logistic-2

朴素贝叶斯分类方法

前言

朴素贝叶斯分类算法是机器学习领域最基本的几种算法之一。但是对于作者这样没有什么数据基础的老码农来说，理解起来确实有一些困难。所以撰写此文帮助自己理解算法，同时也希望对同样在机器学习起跑线上的同仁有所帮助。

开篇我们就不对所涉及的技术要求做说明了，假设您具备高中数学的基础，或者像作者一样，还能回忆起一些数学基础知识，对python语言基础有一定的了解，那么您在阅读本文时就不会有任何困难。

另外，本文参考了《机器学习实战》中第四章《基于概率论的分类方法：朴素贝叶斯》中的内容。这里向作者致以崇高的敬意。

问题

这里我们使用一个例子来一步一步分析，并用python来实现分类算法。

我们假设在某网站的评论区中，我们需要实现对用户的评论进行分类。简单来说，一类为合法的评论，一类为存在不文明用语的评论。我们的问题是，现在管理员工作压力很大，每天要处理数以千计或者数以万计的评论分类，那么我们如何来帮助他们呢？

第一个想到的方法肯定是让机器能够通过评论的内容，自动对评论进行分类。听起来很美，但是实现起来貌似没那么简单。那么接下来，我们来看一下这个最好的但貌似并不简单的想法怎么来实现呢？

解决方法

第一步 样本数据

我们将管理员之前的分类数据提取出来。然后再将我们关心的数据清洗出来，做为我们研究解决方案的样本数据。我们可以将每一条评论中的单词全部提取出来，用来观察这些单词的组合和分类的关系，我们创建一个数组postingList如下：

postingList = [
    ['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
    ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
    ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
    ['stop', 'posting', 'stupid', 'worthless', 'garbage'],
    ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
    ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']
]

这个二维数组的每一行，表示一条评论。这是管理员之前经过很大努力的分类工作成果，那么分类信息呢？请看下面的数据：

classVec = [0,1,0,1,0,1]

我们用这样的一个一维数组来表示上面评论的分类情况。就是说，第一条postingList[0]评论[‘my’, ‘dog’, ‘has’, ‘flea’, ‘problems’, ‘help’, ‘please’]的分类信息是classVec[0]，这里0表示合法评论，1表示不文明用语。

这个样本数据，就形成了我们下面所涉及到的概率计算的样本空间，即下文中设计到的概率，都是在样本数据组成的样本空间中计算得到的。

第二步 应用朴素贝叶斯算法

朴素贝叶斯算法是贝叶斯决策论的一部分，这看起来很高深。貌似没学过，或者老师讲过但是完全忘记了。没关系，我来简单解释一下。朴素贝叶斯就是说，根据数据属于分类的概率，来给数据分类。在我们的问题中，就是我们要计算一下，一个评论可能被评定为合法评论的概率p0和被评定为不文明用语的概率p1这两个概率的大小，哪个概率高就被评定为哪一类。貌似又是一个听起来简单，实现起来很难的问题啊。不用担心，我们接下来一步一步将问题的原理阐明。

这个分类的概率怎么计算呢？这里我们要说明一个概率方面的概念，叫做“条件概率”。具体的数学定义请看这里。严谨的数学概念很难理解和记住，那么我们就以下面的公式符号做个简单说明：

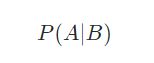
这个条件概率的符号表示，事件B发生的前题下事件A发声的概率。

那么，在我们的问题中，我们要计算的两个概率应该怎么表示呢？首先我们将评论中出现单词组合w事件定义为Ww；被评定为不文明用语，即评论被分为c1类的事件定义为C1；被评定为合法评论，即评论被评定为c0类的事件定义为C0；

p1：评论被评定为不文明用语的概率，如下表示：

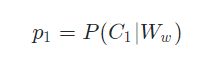
p0：评论被评定为合法评论的概率，如下表示：

又混乱了？好吧。抛开上面那些定义。我们单看p1，根据简单的条件概率的理解。p1表示Ww发生的前提下，C1事件发生的概率。再结合我们的定义，p1就是表示，出现w单词组合的前提下，评论被评定成c1类的概率，即被评定为不文明用语的概率。不难理解，p0就表示出现w单词组合的情况下，评论被评定为合法评论的概率。

说到这里，还是不知道怎么计算这两个概率。不要着急，下面我们接着引入一个贝叶斯准则公式。这个公式的目的是帮助我们在计算条件概率时，来计算条件反转后的概率的。其现实意义可以打个比方，我们已知B事件发生时A事件发生的概率，我们通过这个公式就能够得到，A事件发生时B事件也发生的概率。

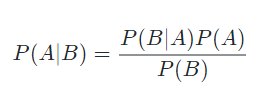
这个准则公式的原理这里就不多介绍了，感兴趣的朋友可以深入了解和验证一下这个公式。这里我们只需要使用这个公式计算我们需要的两个概率值。

套入我们的问题中，p1和p0如下所示：

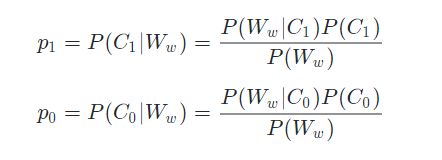
从上面我们推导出的结果可以看出，我们要比较p1和p0的大小，其实比较分子即可，即比较如下两个值：

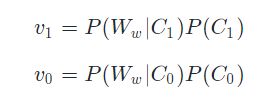
现在，我们距离我们要计算的结果就剩一层窗户纸了。下面让我们来捅破这层窗户纸。

v1和v0计算的过程中，我们看看我们需要的参数。其中，P(C1)和P(C0)分别代表评论被评定成不文明用语和评定成合法评论的概率，我们在样本数据中很容易就可以统计出来。接下来看一下剩下的P(Ww|C1)和P(Ww|C0)如何计算。

我们假定每个单词都是相对独立的，那么一个单词组合出现的概率就等于每一个单词出现的概率相乘。换到条件概率中也是适用的。所以，我们有如下推导：

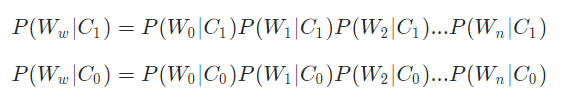
不难看出，我们完全可以在样本数据中，统计出目标评论（我们需要分类的数据）中的每个单词在分类前提下出现的概率。

好了，看来我们找到了计算p1和p0的方法了，确切的说是找到对比它们大小的方法了。我们接下来就可以设计程序了。

第三步 设计程序前简化公式

我们设计的程序的目的是要计算上一步中v1和v0，然后对比大小。由于计算机计算时由于累加或者累乘时，结果超大或者超小造成数据溢出，导致数据不准确。我们对v1和v0进行了取自然对数操作，而取自然对数不会对结果有任何影响。这里提前说明简化公式，以便于理解程序的实现。

我们重新定义v1和v0，如下：

继续推导至评论中每个单词出现的概率：

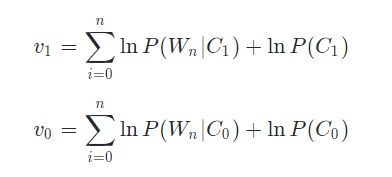
第四步 设计程序
我们可以看到第一步中我们得到的样本数据。

postingList = [
    ['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
    ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
    ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
    ['stop', 'posting', 'stupid', 'worthless', 'garbage'],
    ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
    ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']
]
classVec = [0,1,0,1,0,1]

要想统计各种概率，用这样的样本数据看来是很不适用的，要写很多代码才能实现。那么我们把样本数据转化成一种方便统计的数据结构，其中包含：

一个词表wordlist，样本数据中出现过的所有单词

样本数据每一行评论，对应一个词表向量wordlistVec。这个向量反应词表中单词在评论中出现的情况，因此长度与词表相等。1为出现，0为未出现。例如，我们现在有一个词表[‘my’, ‘dog’, ‘has’, ‘flea’, ‘problems’, ‘help’, ‘please’]，那么评论“my dog has problems”的词表向量就是[1,1,1,0,1,0,0]。我们不难看出词表向量反映出了词表中单词在评论中出现的情况。

一个分类向量classVec，每一个元素表示对应的评论所属的分类
我们把所有的评论的词表向量依次放入一个数组中，形成一个“评论数*词表长度”的矩阵，再配合评论分类向量，结构如下表：

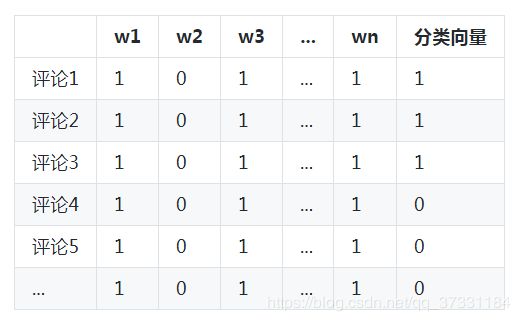
在这样的一个矩阵中，我们就可以研究评论中出现的单词组合和分类之间的规律了。或者说，我们可以通过计算矩阵中0和1的个数，就可以得到我们需要的样本概率。

首先，在bayes.py文件中，我们来写一个函数，用来来准备我们的样本数据：

#coding=utf-8
from numpy import *
def loadDataSet():
    postingList=[['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
                 ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
                 ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
                 ['stop', 'posting', 'stupid', 'worthless', 'garbage'],
                 ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
                 ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
    classVec = [0,1,0,1,0,1]    #1 不文明用语, 0 非不文明用语
    return postingList,classVec

然后，我们写一个函数，通过样本数据中的所有评论生成一个词表：

# 从dataSet中获取一个单词列表(词表)，记录每一个出现过的单词
def createWordList(dataSet):      
    vocabSet=set([])
    for row in dataSet:
        vocabSet = vocabSet|set(row)
    return list(vocabSet)

编写一个能将评论转化为词表向量的函数：

'''
将词表转化成，表示在wordArray中是否出现的向量
返回一个向量，向量的元素为wordList中对应角标单词在数组wordArray中是否出现
1出现
0未出现
'''
def wordList2Vector(wordList,wordArray):
    result=[0]*len(wordList)
    for word in wordArray:
        if word in wordList:
            result[wordList.index(word)] = 1
    return result

这时，我们就可以生成一个所有评论的词表向量矩阵，然后打印一下，查看一下结果：

if __name__=='__main__':
    dataSet,classVec=loadDataSet()
    print '样本数据：',dataSet
    print '分类向量：',classVec
    wordlist=createWordList(dataSet)
    print '词表：',wordlist
    exMat=[]
    for row in dataSet:
        exMat.append(wordList2Vector(wordlist,row))
    print '样本数据的词表向量矩阵：',exMat

我们看一下结果显示：

样本数据： [['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'], ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'], ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'], ['stop', 'posting', 'stupid', 'worthless', 'garbage'], ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'], ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
分类向量： [0, 1, 0, 1, 0, 1]
词表： ['cute', 'love', 'help', 'garbage', 'quit', 'I', 'problems', 'is', 'park', 'stop', 'flea', 'dalmation', 'licks', 'food', 'not', 'him', 'buying', 'posting', 'has', 'worthless', 'ate', 'to', 'maybe', 'please', 'dog', 'how', 'stupid', 'so', 'take', 'mr', 'steak', 'my']
样本数据的词表向量矩阵： [[0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1], [0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0], [1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1], [0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1], [0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0]]

我们在第三步中最后，得到我们要计算的两个值v1和v0:

因为我们只分了2个类型，所以：

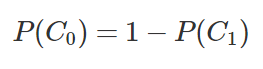
所以我们接下来要实现的函数，计算得到3个结果即可

'''
通过样本数据，计算出分类出现的概率，以及样本数据中每个单词，在每个分类出现的情况下，出现的概率
exampleMat  一个二位数组，每一行表示从样本数据中抽取的词表中每个单词，是否在样本数据中对应行出现，1为出现，0为未出现
exampleCategory 一个一维数组，记录exampleMat中每一行词表出现情况所表示的分类，1为不文明用语，0为文明用语
pAbusive 不文明用语出现的概率
p1 不文明用语分类前提下，每个单词出现的概率向量
p0 文明用语分类前提下，每个单词出现的概率向量
'''
def trainNB0(exampleMat,exampleCategory):
    rowNum=len(exampleMat)
    colNUm=len(exampleMat[0])
    pAbusive=sum(exampleCategory)/float(rowNum) #计算出不文明用语在样本中出现的概率
    p1num=ones(colNUm)
    p0num=ones(colNUm)
    cnt1=2.0
    cnt0=2.0
    for i in range(rowNum):
        if exampleCategory[i]==1:
            p1num += exampleMat[i]
            cnt1 += sum(exampleMat[i])
        else :
            p0num += exampleMat[i]
            cnt0 += sum(exampleMat[i])
    p1=log(p1num/cnt1)
    p0=log(p0num/cnt0)
    return p1,p0,pAbusive

这个函数的返回值中，p1是一个由概率的自然对数组成的向量，每个元素表示词表中每个单词出现的概率（C1条件下）的自然对数。同样p0也是一个道理，只是概率是条件是C0。pAbusive即P(C1)的结果。我们获得整个词表的条件概率的自然对数向量有什么用呢？后面我们会说名的。

注意

p1num=ones(colNUm) 
p0num=ones(colNUm) 
cnt1=2.0 
cnt0=2.0 

这段代码变量的初始值并不是0，这是防止计算后数值过小而产生溢出，不会对结果有任何影响。

下面我们来实现一个负责分类的函数，即一个分类器。这是实现分类的最后一步了，那么输入的参数应该是我们需要分类的评论内容，我们称作目标评论，返回值是分类的值（0或者1）。这里我们用评论的词表向量来代替评论内容，我们称作目标词表向量，即评论的词表向量的分类就是评论的分类。上面我们取得了词表中所有单词的条件概率的自然对数向量p1和p0。用这个向量乘以目标词表向量，就得到目标评论中每个单词的条件概率的自然对数组成的向量（目标评论中没有出现的单词，值为0）。再经过求和运算即得到

def classifyNb(classifyVec,p0vec,p1vec,pc):
    v0=sum(classifyVec*p0vec)+log(pc)   
    v1=sum(classifyVec*p1vec)+log(1.0-pc)
    if(v1>v0):
        return 1
    else:
        return 0

这个函数的第二、三、四个参数，就可以使用我们上面计算出来3个样本空间的概率结果。第一个参数即通过评论内容转化的词表向量。

下面我们来完成验证我们实现的分类器部分的代码：

if __name__=='__main__':
    dataSet,classVec=loadDataSet()
    print '样本数据：',dataSet
    print '分类向量：',classVec
    wordlist=createWordList(dataSet)
    print '词表：',wordlist
    exMat=[]
    for row in dataSet:
        exMat.append(wordList2Vector(wordlist,row))
    print '样本数据的词表向量矩阵：',exMat
    p1v,p0v,pa=trainNB0(exMat,classVec)
    print 'p1:\n',p1v
    print 'p0:\n',p0v
    print 'pa:\n',pa
    testArg=['love','my','dalmation']
    thisdoc=array(wordList2Vector(wordlist,testArg))
    print testArg,'分类结果：',classifyNb(thisdoc,p0v,p1v,pa)
    testArg=['stupid','garbage']
    thisdoc=array(wordList2Vector(wordlist,testArg))
    print testArg,'分类结果：',classifyNb(thisdoc,p0v,p1v,pa)

我们来查看一下结果：

样本数据： [['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'], ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'], ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'], ['stop', 'posting', 'stupid', 'worthless', 'garbage'], ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'], ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
分类向量： [0, 1, 0, 1, 0, 1]
词表： ['cute', 'love', 'help', 'garbage', 'quit', 'I', 'problems', 'is', 'park', 'stop', 'flea', 'dalmation', 'licks', 'food', 'not', 'him', 'buying', 'posting', 'has', 'worthless', 'ate', 'to', 'maybe', 'please', 'dog', 'how', 'stupid', 'so', 'take', 'mr', 'steak', 'my']
样本数据的词表向量矩阵： [[0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1], [0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0], [1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1], [0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1], [0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0]]
p1:
[-3.04452244 -3.04452244 -3.04452244 -2.35137526 -2.35137526 -3.04452244
 -3.04452244 -3.04452244 -2.35137526 -2.35137526 -3.04452244 -3.04452244
 -3.04452244 -2.35137526 -2.35137526 -2.35137526 -2.35137526 -2.35137526
 -3.04452244 -1.94591015 -3.04452244 -2.35137526 -2.35137526 -3.04452244
 -1.94591015 -3.04452244 -1.65822808 -3.04452244 -2.35137526 -3.04452244
 -3.04452244 -3.04452244]
p0:
[-2.56494936 -2.56494936 -2.56494936 -3.25809654 -3.25809654 -2.56494936
 -2.56494936 -2.56494936 -3.25809654 -2.56494936 -2.56494936 -2.56494936
 -2.56494936 -3.25809654 -3.25809654 -2.15948425 -3.25809654 -3.25809654
 -2.56494936 -3.25809654 -2.56494936 -2.56494936 -3.25809654 -2.56494936
 -2.56494936 -2.56494936 -3.25809654 -2.56494936 -3.25809654 -2.56494936
 -2.56494936 -1.87180218]
pa:
0.5
['love', 'my', 'dalmation'] 分类结果： 0
['stupid', 'garbage'] 分类结果： 1

看来我们的分类器还是比较准确的。

总结

以上就是朴素贝叶斯分类算法的原理介绍和简单实现。

更多案例请关注“思享会Club”公众号或者关注思享会博客：http://gkhelp.cn/