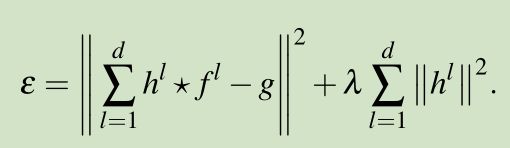DSST (Discriminative Scale Space Tracking) 文章分析（一）
DSST(Discriminative Scale Space Tracking) 是基于 MOSSE，KCF基础上的改进，主要有两个方面：（1）引入多特征融合机制；（2）引入尺度估计。
首先DSST是基于 correlation filter 的方法，相关滤波算法的发展大致可看为：
推荐：https://www.jianshu.com/p/c709aea5a56f （DSST详解）
改进思路
本文中作者（Danelljan）所提出的改进思路有：
（1）多通道应用（特征融合）
首先我们看下MOSSE算法需要优化的方程：
其中变量均在傅里叶域中运算。算法优化目标是：找出一个 filter h 使得均方误差最小。
MOSSE 算法的特征是取自像素的灰度值，也就是单一通道特征，从公式中也可以看出。
再看看DSST 算法的均方误差：
将 patch 特征记为 
， 由 
组成, 对应 
也是由 
组成，同理滤波器 
也由 
组成。作者在这里将patch的特征分为 
个通道。并且上式只与一个patch的 
有关，因此可推广至：
在这个公式中，共与 
个 patch 有关，且每个 patch 均被分为 d 个通道。
（2）Object Tracking 中两个棘手的问题：
目标的定位和目标尺度（尺寸）的改变；
其中目标的尺度变化主要由两方面引起：1：目标沿着相机拍摄轴线方向的运动；2：目标外观的变化；
前者直接影响目标的大小变化；后者可能是目标旋转、平面外运动等的影响。
针对尺度变化，一个简单直接的方法是在多尺度（多分辨率）下估计（预测）目标的外观模型。此时若采用简单穷举的策略，可以使用两种方式的滤波器：
1.joint scale space filter: 一个3维的 filter, 同时对目标的位置和尺度进行评估。
2.multiresolution translation filter: 在多分辨率（多尺度）的候选patch上应用2维标准filter。
作者最终提出的是discriminative scale space tracker: 学习两种滤波器，translation filter 和 scale filter 分别用于评估目标位置和目标尺度。
首先用标准的 translation filter 评估目标的中心位置，然后通过以目标为中心大小可变的patch提取特征进行精确的目标尺度评估。不同于上述提出的两种穷举策略，由于位置的确定，从而减小了搜索区域的大小（确定了目标中心，则无需搜索偏离目标中心的区域）。两 filter 分开学习也可以针对其特点设计不同的特征表示。
a. translation filter（二维）：最终特征为 a*b*28 的特征矩阵，a*b*1为的标准化至[-0.5,0.5]的灰度值，a*b*[2:28]的fHOG特征。
b. scale filter（一维）：最终特征为 z*nScales的特征矩阵, nScales为通道数（尺度数）。作者取4*4为一个cell, 假设当前目标scale大小为a*b ，则 z = a/4 * b/4 * 31。
Scale Factors 尺度因子：
文中用 P*R 表示当前帧目标的初始大小，S 表示 scale filter（一维）的大小，也可以看作尺度的级数，a 为两层之间的比例系数。
取 
, 用于训练的 image patch 
的大小为 
，特征矩阵在上述中已经说明。
大致流程
DSST (以及大部分 Correlation Filters tracking-by-detection framework 的追踪算法) 的大致流程如下：
正如文中所说，Object Tracking 中 我们只知道目标的起始位置。这也就有了进入 tracking-by-detection 循环的切入点。
这里放下论文中的算法流程：
这里说明下文中的 correlation score ：
首先由最小均方误差得到一个解，此时变量均为单通道：
为了避免计算量过大，因此采用 
的近似解, 
称为学习率：
其中 
，用 
来近似求解 。
在MOSSE中，我们可以知道 
，论文中称 y 为相关性分数，提取候选patch 的特征 Z 求出 y ,最终 y 最大值对应的目标 pos 即为当前帧的目标 pos 。
这里作者又提出是否可以不牺牲算法鲁棒性和准确性的前提下减低计算成本，从而增加搜索区域和追踪器，以提高算法的鲁棒性。这也就促进了 fDSST 的提出。
项目地址：http://www.cvl.isy.liu.se/en/research/objrec/visualtracking/scalvistrack/index.html