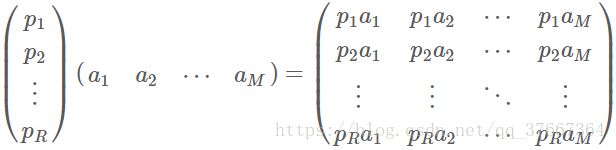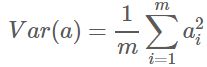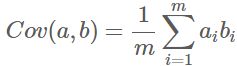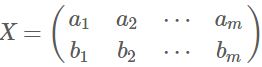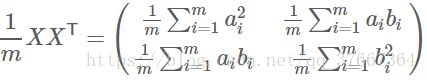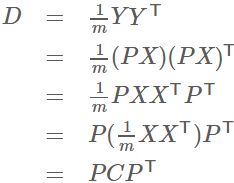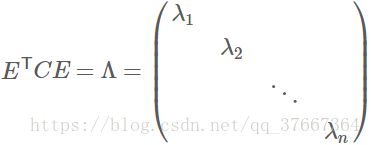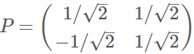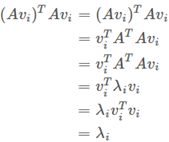PCA原理以及python实现（另外说说SVD奇异值分解）

说明：大部分内容摘自这个链接http://blog.codinglabs.org/articles/pca-tutorial.html，由于没联系到博主，若侵权，望谅解，联系我删除，我觉得原文写得非常好所以分享到这里，算法实现部分以及第3点还有少点杂七杂八的是我自己写的。

 

一.基于最大可分性来解释PCA

(1)简单说明

对于原有的数据我们希望降维后能够尽量的离散，这样能保留原有信息，方差可以衡量离散程度，试想如果有的数据点降维后重叠在一起了，信息就丢失了，如果降低到k维，要做的就是，找到k个方向向量使得把原数据投影到每个方向向量后数据的方差最大，这k个方向向量是k维空间的一组标准正交基

(2)详细说明

一般的，如果我们有M个N维向量，想将其变换为由R个N维向量表示的新空间中，那么首先将R个基按行组成矩阵A，然后将向量按列组成矩阵B，那么两矩阵的乘积AB就是变换结果，其中AB的第m列为A中第m列变换后的结果。

数学表示为：

其中pi是一个行向量，表示第i个基，aj是一个列向量，表示第j个原始数据记录。

特别要注意的是，这里R可以小于N，而R决定了变换后数据的维数。也就是说，我们可以将一N维数据变换到更低维度的空间中去，变换后的维度取决于基的数量。因此这种矩阵相乘的表示也可以表示降维变换。

接下来最关键的问题：如何选择基才是最优的。或者说，如果我们有一组N维向量，现在要将其降到K维（K小于N），那么我们应该如何选择K个基才能最大程度保留原有的信息？

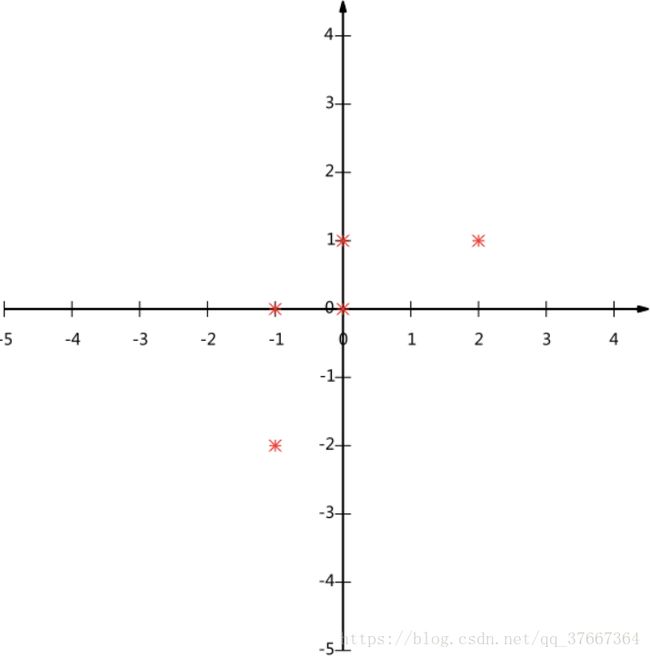
为了避免过于抽象的讨论，我们仍以一个具体的例子展开。假设我们的数据（已经均值归一化）由五条二维记录组成，将它们表示成矩阵形式：

在坐标轴上如图：

 

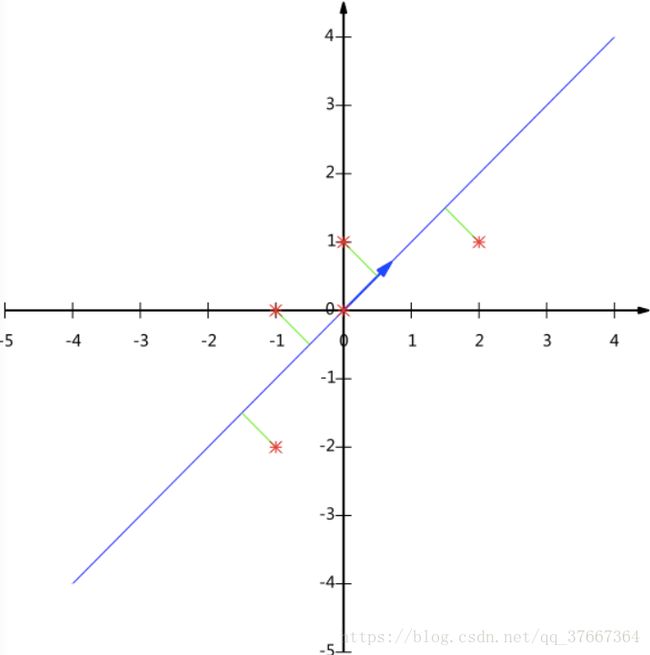
如何选择这个方向（或者说基）才能尽量保留最多的原始信息呢？一种直观的看法是：希望投影后的投影值尽可能分散。

 

以上图为例，可以看出如果向x轴投影，那么最左边的两个点会重叠在一起，中间的两个点也会重叠在一起，于是本身四个各不相同的二维点投影后只剩下两个不同的值了，这是一种严重的信息丢失，同理，如果向y轴投影最上面的两个点和分布在x轴上的两个点也会重叠。所以看来x和y轴都不是最好的投影选择。我们直观目测，如果向通过第一象限和第三象限的斜线投影，则五个点在投影后还是可以区分的。

现在要做的就是最大化投影后的数据间的方差，由于已经均值归一化了所以方差表示如下：

对于上面二维降成一维的问题来说，找到那个使得方差最大的方向就可以了。不过对于更高维，还有一个问题需要解决。考虑三维降到二维问题。与之前相同，首先我们希望找到一个方向使得投影后方差最大，这样就完成了第一个方向的选择，继而我们选择第二个投影方向。

如果我们还是单纯只选择方差最大的方向，很明显，这个方向与第一个方向应该是“几乎重合在一起”，显然这样的维度是没有用的，因此，应该有其他约束条件。从直观上说，让两个变量尽可能表示更多的原始信息，我们是不希望它们之间存在（线性）相关性的，因为相关性意味着两个变量不是完全独立，必然存在重复表示的信息。

数学上可以用两个变量的协方差表示其相关性，由于已经让每个变量均值为0，则：

可以看到，在变量均值为0的情况下，两个变量的协方差简洁的表示为其内积除以元素数m。

当协方差为0时，表示两个变量完全不相关。为了让协方差为0，我们选择第二个基时只能在与第一个基正交的方向上选择。因此最终选择的两个方向一定是正交的。

至此，我们得到了降维问题的优化目标：将一组N维向量降为K维（K大于0，小于N），其目标是选择K个单位（模为1）正交基，使得原始数据变换到这组基上后，各变量两两间协方差为0，而变量的方差则尽可能大（在正交的约束下，取最大的K个方差）。

接下来就说说应用数学如何解决这个问题：

假设我们只有a和b两个变量，那么我们将它们按行组成矩阵X：

然后我们用X乘以X的转置，并乘上系数1/m：

这个矩阵就是协方差矩阵，对角线上的两个元素分别是两个变量的方差，而其它元素是a和b的协方差。

根据上述推导，我们发现要达到优化目前，等价于将协方差矩阵对角化：即除对角线外的其它元素化为0，并且在对角线上将元素按大小从上到下排列，也就是说哪个特征的方差最大我们就保留它对应的基，这样我们就达到了优化目的。这样说可能还不是很明晰，我们进一步看下原矩阵与基变换后矩阵协方差矩阵的关系：

设原始数据矩阵X对应的协方差矩阵为C，而P是一组基按行组成的矩阵，设Y=PX，则Y为X对P做基变换后的数据。设Y的协方差矩阵为D，我们推导一下D与C的关系：

现在事情很明白了！我们要找的P不是别的，而是能让原始协方差矩阵对角化的P。换句话说，优化目标变成了寻找一个矩阵P，满足P*C*PT是一个对角矩阵，并且对角元素按从大到小依次排列，那么P的前K行就是要寻找的基，用P的前K行组成的矩阵乘以X就使得X从N维降到了K维并满足上述优化条件。

由上文知道，协方差矩阵C是一个是对称矩阵，在线性代数上，实对称矩阵有一系列非常好的性质：

1）实对称矩阵不同特征值对应的特征向量必然正交。

2）设特征向量λ重数为r，则必然存在r个线性无关的特征向量对应于λ，因此可以将这r个特征向量单位正交化。

由上面两条可知，一个n行n列的实对称矩阵一定可以找到n个单位正交特征向量，设这n个特征向量为e1,e2,⋯,en，我们将其按列组成矩阵：

则对协方差矩阵C有如下结论：

其中Λ为对角矩阵，其对角元素为各特征向量对应的特征值（可能有重复）

以上结论不再给出严格的数学证明，对证明感兴趣的朋友可以参考线性代数书籍关于“实对称矩阵对角化”的内容。

到这里，我们发现我们已经找到了需要的矩阵P：

P是协方差矩阵的特征向量单位化后按行排列出的矩阵，其中每一行都是C的一个特征向量。如果设P按照Λ中特征值的从大到小，将特征向量从上到下排列，则用P的前K行组成的矩阵乘以原始数据矩阵X，就得到了我们需要的降维后的数据矩阵Y。

最后再说说pca在做的就是：假如我们有m个n维的样本数据，那么我们做的就是先挑出第一个特征，这组特征投影到一个基向量后方差最大，再挑出第二个特征，投影到一个与之前基向量正交的基向量后方差最大，直到第k个，也就是降维为只有m个k维的样本

总结一下PCA的算法步骤：

设有m条n维数据。

1）将原始数据按列组成n行m列矩阵X

2）将X的每一行（代表一个属性变量）进行零均值化，即减去这一行的均值

3）求出协方差矩阵C=1/mXXT

4）求出协方差矩阵的特征值及对应的特征向量

5）将特征向量按对应特征值大小从上到下按行排列成矩阵，取前k行组成矩阵P

6）Y=PX即为降维到k维后的数据

下面是一个例子：将下面这个矩阵降到一维

直接求协方差矩阵：

求解后特征值为：

对应的特征向量分别是：

标准化后特征向量为：

因此我们的矩阵P是：

最后我们用P的第一行乘以数据矩阵，就得到了降维后的表示：

投影后为：

(3) 注：降维后保留了原特征的数据的百分之多少（也可称为解释率）可以由下面的公式计算：

一般而言，设λ1，λ2，λ3…λn表示协方差矩阵的特征值（按由大到小顺序排列），使得λj为对应于特征向量uj的特征值。那么如果我们保留前k个成分，则保留的方差百分比可计算为：

二.PCA与SVD

SVD（Singular Value Decomposition奇异值分解）是一种矩阵分解的方法，目的很明确，就是将矩阵A分解为三个矩阵UΣVT的乘积的形式，我们不妨接着PCA的步骤往下做。 我们有A=BVT，我们将B写成归一化的形式，其拆开成B=UΣ，其中U的每一列是单位向量，而Σ=diag{σ1,σ2,⋯,σn}则是B中每个向量的模长且σ1>σ2>⋯>σn。而B中每一列的模长为|Avi|，由于vi是 的特征向量，对应特征值为λi，那么Avi平方为

 = ，这是特征向量的定义

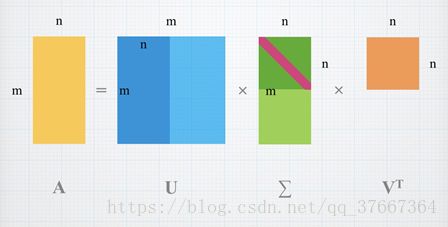
所以有|Avi|= ，所以将B写成B=UΣ的形式后，U是正交矩阵，而Σ是一个对角阵，其每一个元素σi= 。 我们再来看SVD的图示：

从图中看出，中间的奇异值矩阵由大到小排列，越后面的值对结果的影响越小，因此，如果只保留较大的奇异值和其对应的U、V中的向量，对于矩阵压缩则能起到很好的作用。在该例子中，m>n，能通过得出的ui只有n个，剩下m-n个基直接随便找正交基补全即可，他们在计算中实际上也没什么用。 我们把SVD分解的结果带入协方差矩阵：

可以看出，中间那个U消掉了，这也能部分反映SVD和PCA间的关系。

实际上：

假如我们有m个n维特征的样本，构成矩阵X，PCA就是在对X的协方差矩阵进行特征分解，而SVD直接对X进行分解，SVD不用先求出协方差矩阵

三.为何要引入SVD？

之前我也在想这个问题，既然方阵都能特征分解，而在PCA中我们分解的就是一个协方差方阵，那还使用SVD干嘛？用特征分解实现pca算法时我才知道，对于有的协方差矩阵特征值会是虚数，这种情况算法会失效，而SVD奇异值分解得到的奇异值一定是非负实数,可以解决之前的情况！矩阵的知识不是很扎实，没有详细学过svd，有时候总感觉不明不白的。。。

四.python实现

算法细心一点也挺好写的，但是我没写svd分解的版本，只是简单写了特征分解的版本。

# coding: utf-8

'''
特征向量分解实现PCA算法
如果特征值出现复数该算法会失效，这就引入了SVD，奇异值分解，
奇异值类比于特征值，但是奇异值一定是非负实数，不存在之前的情况
'''

import numpy as np
class PCA(object):
    m = 0
    n = 0
    #降维所需的基向量
    base_vectors = None
    #均值归一化
    def mean_normalization(self,X):
        for j in range(self.n):
            me = np.mean(X[:,j])
            X[:,j] = X[:,j] - me
        return X
    #r为降低到的维数
    def fit(self,X,r):
        self.m = X.shape[0]
        self.n = X.shape[1]
        #均值归一化
        X = self.mean_normalization(X)
        Xt = X.T
        #协方差矩阵
        c = (1/self.m) * Xt.dot(X)
        print(c)
        #求解协方差矩阵的特征向量和特征值
        eigenvalue,featurevector=np.linalg.eig(c)
        #对特征值索引排序 从大到小
        aso = np.argsort(eigenvalue)
        indexs = aso[::-1]
        print("特征值:",eigenvalue)
        print("特征向量:",featurevector)
        print("降为",r,"维")
        eigenvalue_sum = np.sum(eigenvalue)
        self.base_vectors = []
        for i in range(r):
            print("第",indexs[i],"特征的解释率为:",(eigenvalue[indexs[i]] / eigenvalue_sum))
            self.base_vectors.append(featurevector[:,indexs[i]])#取前r个特征值大的特征向量作为基向量
        self.base_vectors = np.array(self.base_vectors)
        return
    
    def transform(self,X):
        #r*n的P乘以n*m的矩阵转置后为m*r的矩阵
        return self.base_vectors.dot(X.T).T
    def fit_transform(self,X,r):
        self.fit(X, r)
        return self.transform(X)
    
#测试
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data.T
pca = PCA()
X_transformed = pca.fit_transform(X, r=1)