网络流量与布雷斯悖论 1160300929 郑子豪

现实生活中的好多问题都可以用博弈论的知识去解释，比如在交通运输网络中行驶或者是互联网传送数据包，每个人都需要根据自己或他人的选择来对路线进行评估，最后做出最终选择。

在开车的时候，有的人觉得如果在起点和终点之间加入一些路径，会让从起点到终点的时间缩短。这是非常朴素的思维，不使用博弈论的手段进行分析的话，你可能永远都认为这是对的，实际上，在分析网络流量模型的时候，会发现一个悖论，增加网络容量可能反而会减慢网络流通的速度。

我们首先构建一个运输网络的模型，观察网络如何应对网络拥塞。在此基础上，进一步引人博弈论的思想来讨论有关问题。用有向图表示一个运输网络：边表示高速公路，节点表示进人或离开髙速路的出人口。假设有两个特别的节点 A和B，每个人都要从 A开车到 B。可以想象， A是城郊附近的一个出人口，B是市中心的一个出人口，我们要分析上下班高峰期的车辆行驶情况。最后，根据当前交通M，每条边都有一个特定的行程时间。为使这个问题更为具体化，参见图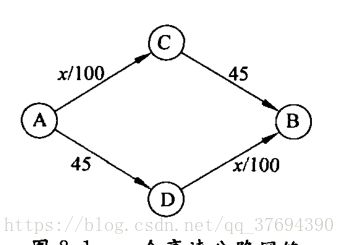

。每条边都标记出当有:t辆车行驶时的行程时间（以分计算）。简单举个例子，A-D和C-B边并不受交通状况影响：无论有多少辆车行驶在其中，都需要45分钟穿越。相比之下，A-C和D-B边受拥堵的影响较大：当有x辆车行驶在同一条路线时，穿越该路线所需要的时间为x/100分钟。①

现在,假设有4000辆车希望在早晨上班时能从节点A行驶到B。每一辆车有两种可能的路线：通过C的路线或者通过D的路线。假设每辆车都选择上面的路线(通过C),那么每辆所需用的总时间为85分钟，即4000/100 + 45 = 85。如果每辆车都选择下面的路线，结果也是一样。然而，如果所有的车被均分到两条路线，每条路线承载2000辆车,那么两条路线每辆车所需的时间为2000/10+45 = 65。这实际上就是一场博弈，参与者相当于司机，每个参与者的可能的策略是从A到B的可能路线。在这个流量博弈中，通常没有占有策略，但是存在纳什平衡，如果司机能够等可能的选择两条路线，就能够形成纳什平衡，而且这是形成纳什平衡的唯一条件。因为如果两条路上的车不一样多，那么较慢路线上的司机就会想换到较快的车道上，因此只有x=2000才能形成纳什平衡。

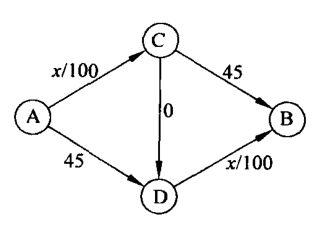
当我们想要改变现状，对这个网络进行小小的改变，就会形成一个有悖常理的状态。

我们做如下改变:假设市政府计划从C到D新建一条高速公路,如上图所示。为了使事情简单化,设它的行程时间为0,不管有多少辆车在此路线上都一样,尽管由此产生的效果有别于实际情况(但影响应该很少)。按常理推断C到D的路建成后,A到B的运行时间会减少很多。

 实际结果令人吃惊:在这个新的高速网络中存在一个唯一的纳什均衡,但是它导致大家花费更多的行驶时间。均衡状态下，下,每个司机都使用从C到D的路线,结果每个司机需要的行驶时间为4000/100 +0 + 4000/100=80。进一步分析为什么这是一个均衡,注意到此时没有司机能从改变路线中受益:有了从C到D的路线后,其他任何一条路线都需花费85分钟。那么为什么说这是唯一的均衡?可以看到,从C到D路线的建立事实上使此路线成为所有司机的占优策略:不管当前的流量模式是什么，换到从C到D的路线都会受益。

换句话说,一旦由C到D的高速路建成，此路线就像一个漩涡,将所有司机都吸引至此,这对所有人都有害。在新的网络中,如果所有司机的行为都是自我利益占优,就没有办法使网络恢复到一个对大家都更好的等分情况。
 这种现象,即一个运输网络增加新的资源有时反而使均衡状态中的性能受损,最早布雷斯在1968年就已提出 ,随后被称为布雷斯悖论。就像很多有悖常理的异常现象,它们的出现是基于实际生活中各种条件的恰当结合。  在实际的运输网络中也曾经被观察到,韩国首尔市曾拆毁一条有6条行车道的高速路而改建成一个公园,实际上反而减少了出人该城市的交通时间。