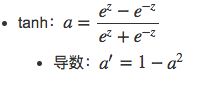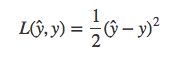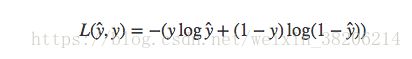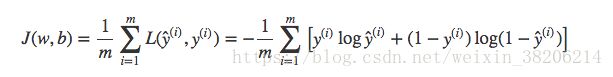神经网络基础-多层感知器(MLP)

DL教程 http://study.163.com/courses-search?keyword=%E5%90%B4%E6%81%A9%E8%BE%BE#/?ot=5

原文：https://blog.csdn.net/weixin_38206214/article/details/81137911

一、前言

多层感知器(Multi-Layer Perceptron，MLP)也叫人工神经网络(Artificial Neural Network，ANN)，除了输入输出层，它中间可以有多个隐层。最简单的MLP需要有一层隐层，即输入层、隐层和输出层才能称为一个简单的神经网络。习惯原因我之后会称为神经网络。通俗而言，神经网络是仿生物神经网络而来的一种技术，通过连接多个特征值，经过线性和非线性的组合，最终达到一个目标，这个目标可以是识别这个图片是不是一只猫，是不是一条狗或者属于哪个分布。

由于最近在复现别人论文，中间插入一下自己对多层感知器的一些想法，如出现错误欢迎批评指正，共同学习。首先多层感知器对于我的理解是多层，大于等于3层，主要是3层，如果想把两个向量x1和x2进行感知首先要把两者分别非线性的转换到一起。非线性如何实现呢，根据观察到的多片博客，主要是使用激活函数。当然激活函数的选择也是有部分影响的，根据测试得到的，在我这里误差不是很大。

二、计算神经网络的输出

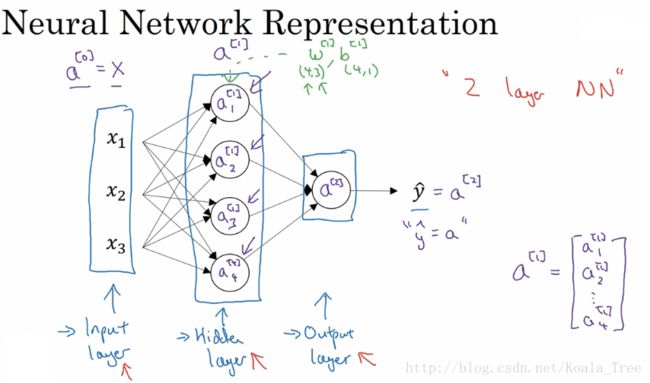
接下来，我们给出一个单隐层的神经网络，以此来看一下神经网络的具体流程。大致模型如图所示：

首先我们先对图中的参数做一个解释：

其中，第0层(输入层)，我们将x1，x2和x3向量化为X；

0层和1层(隐层)之间，存在权重w1(x1到各个隐层)，w2...w4，向量化为W[1]，其中[1]表示第1层的权重，偏置b同理；

对于第1层，计算公式为：

Z[1] = W[1]X + b[1]

A[1] = sigmoid(Z[1])

其中Z为输入值的线性组合，A为Z通过激活函数sigmoid的值，对于第1层的输入值为X，输出值为A，也是下一层的输入值；

1层和2层(输出层)之间，与0层和1层之间类似，其计算公式如下：

Z[2] = W[2]A[1] + b[2]

A[2] = sigmoid(Z[2])

yhat = A[2]

其中yhat即为本次神经网络的输出值。

为什么要用激活函数
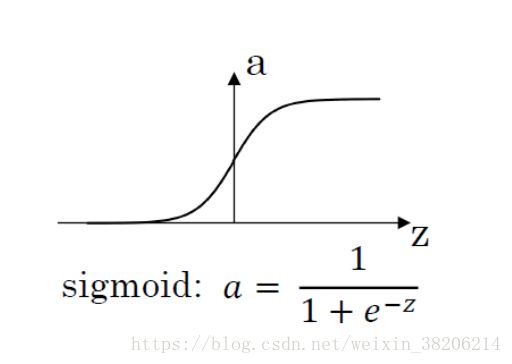
根据输出的计算可以发现，其实隐层的每个神经元是由输入特征x的线性组合构成。然而如果仅仅是线性组合，那么不管这个神经网络有多少层，结果都将与特征线性相关。于是我们在每个神经元结果z之后，添加一个激活函数(Activation Function)，改变线性规则，比如使用Sigmoid函数，公式如下：

在Sigmoid函数中，a的值在[0,1]之间，我们可以将其理解为一个阀。就像是人的神经元一样，当我们一个神经元受到的刺激时，我们并不是立刻感觉到，而是当这个刺激值超过了阀值，才会让神经元向上级神经元发出信号。

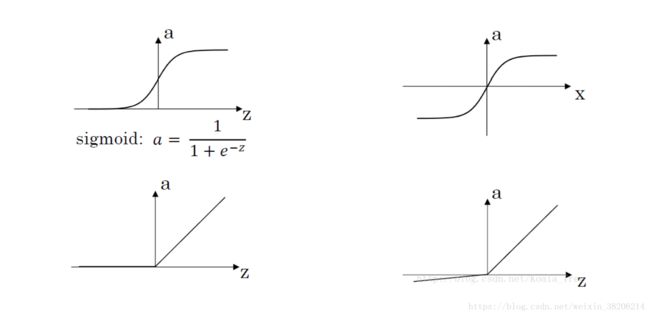
接下里我们给出常用的几个激活函数以及其图像：

图上左上角，即为上文所述的sigmoid函数，其导数为a· = a(1 - a)

右上角为tanh函数：

左下角为ReLU(修正线性单元)：a = max(0，z)

右下角为Leaky ReLU：a = max(0.01，z)

对于激活函数的选择，是神经网络中很重要的一步，对比sigmoid函数和tanh函数在不同层的使用效果：

隐藏层：tanh函数的表现要好于sigmoid函数，因为tanh的取值范围在[-1，1]之间，均值为0，实际上气到了归一化(使图像分布在0周围，得到的结果更方便使用梯度下降)的效果。
输出层：对于二分类而言，实际上是在计算yhat的概率，在[0，1]之间，所以sigmoid函数更优。
然而在sigmoid函数和ReLU函数中，当Z很大或很小时，Z的导数会变得很小，趋紧于0，这也称为梯度消失，会影响神经网络的训练效率。

ReLU函数弥补了二者的缺陷，当z>0时，梯度始终为1，从而提高神经网络的运算速度。然而当z<0时，梯度始终为0。但在实际应用中，该缺陷影响不是很大。

Leaky ReLU是对ReLU的补偿，在z<0时，保证梯度不为0。

总结而言

在选择激活函数的时候，如果不知道该选什么的时候就选择ReLU，当然具体训练中，需要我们去探索哪种函数更适合。

四、损失函数

在神经网络的训练中，我们通过损失函数(Loss Function)来衡量这个神经网络的训练是否到位了。

一般情况下，使用平方差来衡量：

事实上，我们一般不使用平方差来作为二分类问题的损失函数，因为平方差损失函数一般是非凸函数，我们可能会得到局部最优解，而不是全局最优解。因此我们选择如下函数：

 

其实，y为样本真实值，yhat为样本预测值；

当y=1时，yhat越接近1，L(yhat，y)越接近0，表示预测效果越好；

当y=0时，yhat越接近0，L(yhat，y)越接近0，预测效果越好。

那么我们的目标即为使损失函数到达最小值，其中损失函数针对单个样本。

代价函数(Cost Function)

全部训练数据集的损失函数的平均值，即为训练集的代价函数：

根据上述公式，可以发现代价函数其实是w和b的函数，实际上我们的目标是迭代来计算出最佳的w和b的值(矩阵)，使代价函数最小化(接近0)，也就是最好的训练结果。