计算机网络6————加密算法和Https

计算机网络6————加密算法和Https

一.概述

前两天接连面试腾讯，阿里一面。都被问到了https相关的内容，答得并不满意，所以就打算将其相关的内容整理总结。

在说https之前，先说一下加密算法相关的内容

二.加密算法

加密算法分为两种：即对称加密和非对称加密。

1.对称加密

对称加密：对于对称加密来说。它的加密和解码的密钥是相同的。也就是说：明文加密成密文，和密文解密成明文使用的是同样的秘钥。

对称加密的优点：

• 使用起来快捷简单
• 秘钥较短，且破译困难

对称加密在使用时，存在的问题：

• 在进行通信前，要求双方建立一条可靠的通道来传输密钥
• 密钥的数目难于管理，因为对于每一个合作者(客户端)，都需要使用不同的密钥
• 对称加密算法一般不能提供信息的完整性鉴别，即无法验证发送者和接受者的身份
• 对称密钥的管理和分发也是一间具有潜在危险和繁琐的过程

常见的对称加密算法：DES、3DES、Blowfish、IDEA、RC4、RC5、RC6和AES

2.非对称加密

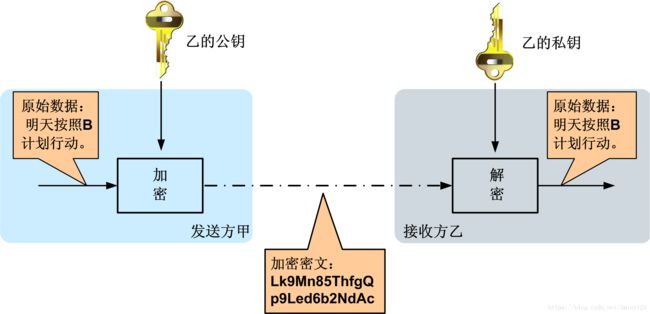
非对称加密技术需要两个密钥，公钥和私钥成对出现。
公钥和私钥的作用：公钥加密的内容，私钥可以解密，反之私钥加密的内容，公钥可以解开。
非对称加密的基本过程：

• 乙生成一对秘钥，公钥可以发送给所有人，私钥自己保存。
• 甲通过公钥将明文加密成密文。（此时其他人获取该信息，如果没有私钥则无法破解）、
• 乙获取的到甲发送的密文，根据自己持有的私钥来进行解密
• 乙此时返回消息时，使用自己的私钥加密，发送给甲（此时其他人获取该信息，有可能破解该信息，因为公钥是公开的）
• 甲获取到乙的密文，根据公钥进行解密，获取明文

非对称优点：

• 安全

非对称缺点

• 非对称最大的确定就是速度太慢

场景的非对称加密算法：：RSA、ECC（移动设备用）、Diffie-Hellman、El Gamal、DSA（数字签名用）。

下面简单来看一下一个比较简单的非对称加密算法，RSA加密算法。

三.RSA加密算法

1.需要的数论知识

a.互素数

互素数是指，两个公约数只有1的两个数，叫做互素数
关于互素数的结论

1.任意两个质数构成互质关系，比如13和61。
2.一个数是质数，另一个数只要不是前者的倍数，两者就构成互质关系，比如3
3. 如果两个数之中，较大的那个数是质数，则两者构成互质关系，比如97和57。
4. 1和任意一个自然数是都是互质关系，比如1和99。
5.p是大于1的整数，则p和p-1构成互质关系，比如57和56。
6. p是大于1的奇数，则p和p-2构成互质关系，比如17和15。

b.欧拉函数
欧拉函数$\varphi (n)$是指：任意给定正整数n，求小于n的正整数之中，有多少个和n构成互质关系。这个数量即欧拉函数的值

关于欧拉函数的结论很多，我们只需要了解其中两条

• 如果n 是两个质数 p q的乘积，即n = p * q，则一定有下面等式成立
  $$\varphi (n)=(p-1)\ast (q-1)$$
  即，小于n并且和n互素的数，一共有 (p - 1)*(q-1) 个

• 如果n和e互素的，则一定满足下面的关系式（费马-欧拉定理）
  $$e^{\varphi (n)}\%n=1$$

c.模反元素
如果两个正整数a和n互质，则一定存在一个正整数d，使的下面等式成立
$$a\ast b\%n=1$$
即 a和b的乘积对n取余的结果为1

基本的数学铺垫完成，接下来看看公钥和私钥的生成

2.公钥和私钥的生成

• 第一步： 寻找两个大素数，p,q
  • p = 3 ,q = 5
• 第二步： n = p * q
  • n = 15
• 第三步： 计算n的欧拉函数$\varphi (n)=(p-1)(q-1)$
  • ($\varphi (n)=8$ )
• 第四步：在（0，n）范围内，寻找一个和n互素的数，e。此时e一定满足$e^{\varphi (n)}\%n=1$
  • （e = 7）
• 第五步：寻找一个数d，使 $ed\%\varphi (n)=1$ 。d一定存在，并且可能存在多个
  • 求出一个d ，d = 13
• 第六步：求出公钥公钥(e , n) 私钥是(d ,n)
  • 公钥（7,15），私钥（13，15）

注意：在计算过程中的，p和q不能泄露，防止直接计算出$\varphi (n)$值，然后猜想出d的值。
另外：3,4,5步骤的数学原理，在上面有简单提过

3.加密和解密的过程

m：明文，c：密文
加密公式：
$$c=m^e\%n$$

解密公式
$$m=c^d\%n$$

举例:用上面的公钥秘钥对 2进行加密解密
加密：
$$2^7\%15=8$$

解密：
$$8^{13}\%15=2$$

4.加密解密过程的验证

下面我们来证明一下，明文可以通过上面的步骤，来进行加密和解密，即证明两个式子是等价的:

加密过程：
$$c=m^e\%n$$
从上面的式子，可以得到：
$$c=n的倍数+m^e$$
等式两边同时d次方：
$$c^d=(n的倍数+m^e{)}^d$$
可以转换为下面的式子，注意上下的倍数可能不同：
$$c^d=n的倍数+m^{ed}$$

根模反函数可得下面的式子，t也是未知，表示倍数：
$$c^d=n的倍数+m^{\varphi (n)的倍数+1}$$

转换为：
$$c^d=n的倍数+m\ast m^{\varphi (n)的倍数}$$

根据费马欧拉定理可得：
$$c^d=n倍数+m\ast (1+n的倍数)$$

整理得：
$$c^d=n的倍数+m$$

即：
$$c^d\%n=m$$

四.Hash算法

hash算法，也是一个很常见的检验算法，但不是一个加密算法，我们常说的md5，就是hash算法的一种。下面来简单的看一看hash算法。

1.哈希概述

哈希函数，也称为散列函数或者杂凑函数。哈希函数是一个公开函数。可以将任意长度的消息m映射为一个长度较短的固定值H（M），他是一种单向密码体制，即一个明文到密文的不可逆映射，只有加密过程，没有解密过程

无论输入是什么格式，文件有多大，输出都是固定长度的比特串。以比特币使用的Sh256算法为例，无论输入是什么数据文件，输出的都是256bit

2.哈希与加密的区别

其实从上面的哈希概述中就能看出，哈希与加密的两个重要的区别：

• 哈希算法往往被设计成具有相同长度的文本，而加密算法生成的文本长度与明文本身的长度有关
• 哈希算法是不可逆的，而加密算法的是可逆的
  • 哈希算法不可逆，有两重含义，一是指给定一个哈希结果R，没有办法将E转换为文本S。二是知道一段文本S的结果为R，但是不能听说S一定是R的
  • 加密算法可以， 给定加密后的密文R，存在一种方法可以将R确定的转换为加密前的明文S。

3.哈希与加密的数学基础

哈希算法$R=H(S)$是一个多对一映射，给定目标文本S，H可以将其唯一映射为R，并且对于所有S，R具有相同的长度。由于是多对一映射，所以H不存在逆映射$S=H^{-1}$。

解密算法$R=E(S,K_E)$是一个一一映射，其中第二个参数就是加密密钥，E可以将给定的明文密钥$K_e$唯一映射为密文R，并且存在另一个一一映射$S=D(R,K_D)$,可以结合$K_d$将密文R唯一映射为明文S，其中$K_d$叫做解密密钥。

但是符合上面的定义的映射仅仅可以被叫做哈希算法和加密算法，但未必是好的哈希和加密，好的哈希和加密往往需要需要满足下面比较贱

一个好的哈希算法：
一个设计良好的哈希算法应该很难从哈希结果找到哈希目标文本的碰撞。一个好的哈希应该对输人的变化及其敏感，即使有危险的改动了，比如一亿个字符改变了一个字符，那结构也也应该不同

碰撞是指，如果$S_1̸=S_2,H(S_1)=H(S_2)$,则S1和S2互为碰撞。

一个好的加密算法：
一个设计良好的加密算法，应该是一个“单向陷门函数”，即一般情况下，即使知道函数本身也很难将函数的值换回函数的自变量，具体到加密就是说很难从密文得到明文，虽然理论可以，而陷门是一种特殊的元素，一旦知道陷门，则这种逆转换是很容易进行的，具体到加密算法，陷门就是秘钥。

4.哈希和加密的选择

要实现数据的保护，可以选择哈希或加密两种方式，那么什么时候惦哈希，什么时候选择加密呢

基本原则：如果被保护的数据仅仅用作比较验证，之后不需要还原成明文形式，则使用哈希。如果被保护的数据在以后还需要被还原成明文，则需要使用加密。

5.哈希的特点

下面总结一下哈希算法的特点：

• 易压缩：对应任意长度的x，Hash值的长度很小
• 易计算：对于任意给定的消息，计算其Hash值比较容易。
• 单向性：对于给定的Hash值，要找到使得在计算上是不可行的，即求Hash的逆很困难。在给定某个哈希函数H和哈希值H（M）的情况下，得出M在计算上是不可行的。即从哈希输出无法倒推输入的原始数值。这是哈希函数安全性的基础。
• 抗碰撞性：理想的Hash函数是无碰撞的，但在实际算法的设计中很难做到这一点。

六.数字证书

1.数字签名

数字签名是什么（公钥数字签名，电子签章），用于鉴别数字信息的方法，一套数字签名通常定义了两种互补的起那么。

签名作用 :数字签名对于原文的保密性没有要求，但是负责两件事：发送者的身份，发送的内容是否完整

签名原理：发送的内容是否完整，可以使用上面说的哈希算法，生成一段摘要 。根据再要来验证内容是否完整。而身份的验证，可以使用我们前面说的非对称加密算法(可以使用RAS)。发送者可以使用自己的私钥对摘要进行加密。接收者根据公钥，来进行解密。解密成功，确认发送者。

一次完整的签名过程
A为发送者，B为接收者

• A对外发布公钥，并声明私钥在自己手上
• A对发送的消息M根据hash算法计算摘要，得到摘要D
• A用私钥对D进行签名，得到签名S
• 将M和S一起发送出去

验证过程

• B对M根据同样的hash算法计算摘要，得到摘要D1
• 使用A发布的公钥对S进行解密，得到D
• 如果D和D1相同，说明M确实是小明发出的，并且没有被篡改过

数字签名的问题
在这个过程中，存在一个漏洞，那就B验证A身份时，使用的A的公钥进行验证。在这个过程中可能存在问题。

• 假如有一个C，它伪造了A的一对公钥和私钥。并将伪造后的公钥发给B
• 此时C伪装A发布消息，并根据自己的私钥生成数字签名，发给B
• 此时B根据C伪装的公钥，无法验证发送消息的发送人

对于这个问题的解决，就需要数字证书的加入

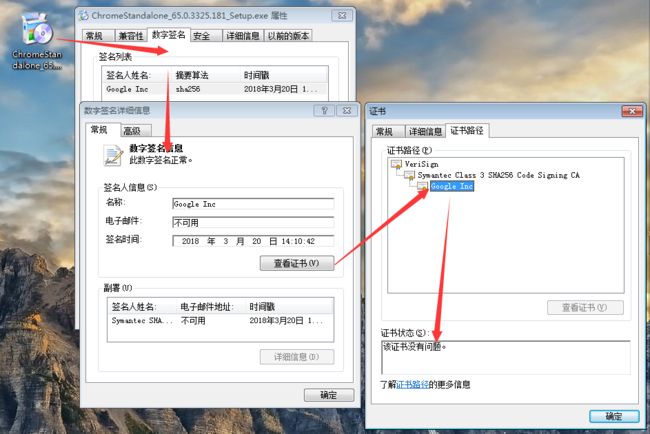
2.数字证书

为了解决上面的问题，即保证B收到的公钥一定是A发出了的。所以引入了一个证书中心（CA机构），为A的公钥做认证。具体的方法就是，用该CA机构使用自己的私钥对A的公钥进行加密生成“数字证书”

证书的获得

• A去找CA证书中心，提供公钥，组织信息，个人信息（域名）等信息，申请认证
• CA通过通过线上，线下多种手段验证申请者提供的身份真实性，向申请者发送认证数字证书
• 数字证书包含的内容:A公钥内容，签发者id，Subject—-也就是这个证书签发给谁，有效期 有效期，其他信息。以上是明文，我们称为内容P。
• 用P进行hash计算，得到一个hash值H，然后使用签发机构的私钥对H进行RSA加密，得到签名信息S。
• 将明文P和签名H，连着一起，就是数字证书

证书的发送

• 证书的发送，在上面A向B发送公钥的时候，将自己获取的证书一同进行发送，让B可以确定这是A发送的公钥

证书的验证

• B收到证书时，用CA的公钥解密这份数字证书，拿到A的公钥，然后验证数字签名，后面流程就和图1的流程一样了，

证书的问题

• 假设数字证书被伪造了
  • 如果对于当前的证书，不信任，可以一直去请求给当前CA做保证的上一级CA，这样子一直递归查询，知道找到一个跟CA机构
  • 跟CA机构的公钥，一般直接写入到了操作系统的低层中，保证其可靠性

下面是一个数字签名和证书的示例

七.HTTPS

前置基础基本已经铺垫好了，现在正是进入正题——Https

1.概述

在之前的文章里，我们详细介绍过HTTP，HTTP发出的内容是明文，任何人都可以通过抓包获取获取到，非常的不安全。

所以为了保护发送报文的安全性，所以提出了HTTPS，HTTPS是密文传输。一般难以获取报文。

简单的说，HTTPS = HTTP +SSL/TSL
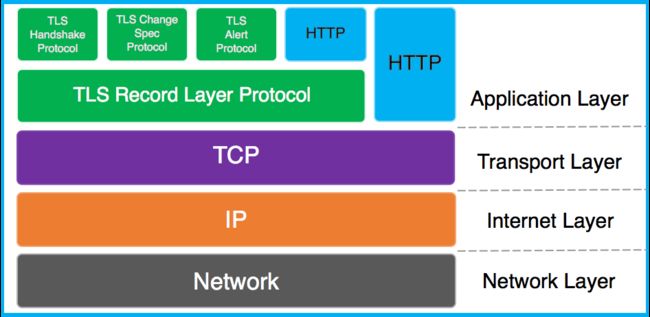HTTPS的加密是将对称加密和非对称加密结合起来，非对称加密用于HTTPS的连接，身份的校验，传输对称加密的秘钥。对称加密连接建立后传输包。

HTTPS同HTTP相比提供了：

• 数据的完整性：内容经过完整性校验（哈希算法）
• 数据隐私性：内容经过对称加密，每一个连接生成唯一的加密秘钥
• 身份认证：通过数字证书，使得第三方无法冒充服务端的身份

2.SSL和TLS

上面我们我们说HTTPS = HTTP +SSL/TSL。那我们来看看，SSL和TLS是什么

SSL即Secure Socket Layer(安全套接字层），为Netscape所研发。是保证数据安全技术，目前是SSL3.0版本
为于可靠的面向连接的网络层协议(TCP)和应用层协议之间的一种协议层。SSL通过互相认证、使用数字签名确保完整性、使用加密确保私密性，以实现客户端和服务器之间的安全通讯。该协议由两层组成：SSL记录协议和SSL握手协议。。

TLS（Transport Layer Security，传输层安全协议），位于两个应用程序之间提供保密性和数据完整性。该协议由两层组成：TLS记录协议和TLS握手协议

两种其实是一种并列关系，即最新版本的TLS是IETF制定的一种新的协议，它建立在SSL 3.0协议规范之上，是SSL 3.0的后续版本。在TLS与SSL3.0之间存在着显著的差别，主要是它们所支持的加密算法不同，所以TLS与SSL3.0不能互操作。

两者的差异：

TLS与SSL的差异
1）版本号：TLS记录格式与SSL记录格式相同，但版本号的值不同，TLS的版本1.0使用的版本号为SSLv3.1。
2）报文鉴别码：SSLv3.0和TLS的MAC算法及MAC计算的范围不同。TLS使用了RFC-2104定义的HMAC算法。SSLv3.0使用了相似的算法，两者差别在于SSLv3.0中，填充字节与密钥之间采用的是连接运算，而HMAC算法采用的是异或运算。但是两者的安全程度是相同的。
3）伪随机函数：TLS使用了称为PRF的伪随机函数来将密钥扩展成数据块，是更安全的方式。
4）报警代码：TLS支持几乎所有的SSLv3.0报警代码，而且TLS还补充定义了很多报警代码，如解密失败（decryption_failed）、记录溢出（record_overflow）、未知CA（unknown_ca）、拒绝访问（access_denied）等。
5）密文族和客户证书：SSLv3.0和TLS存在少量差别，即TLS不支持Fortezza密钥交换、加密算法和客户证书。
6）certificate_verify和finished消息：SSLv3.0和TLS在用certificate_verify和finished消息计算MD5和SHA-1散列码时，计算的输入有少许差别，但安全性相当。
7）加密计算：TLS与SSLv3.0在计算主密值（master secret）时采用的方式不同。
8）填充：用户数据加密之前需要增加的填充字节。在SSL中，填充后的数据长度要达到密文块长度的最小整数倍。而在TLS中，填充后的数据长度可以是密文块长度的任意整数倍（但填充的最大长度为255字节），这种方式可以防止基于对报文长度进行分析的攻击。

下面说一下，基于SSL的HTTPS的请求过程

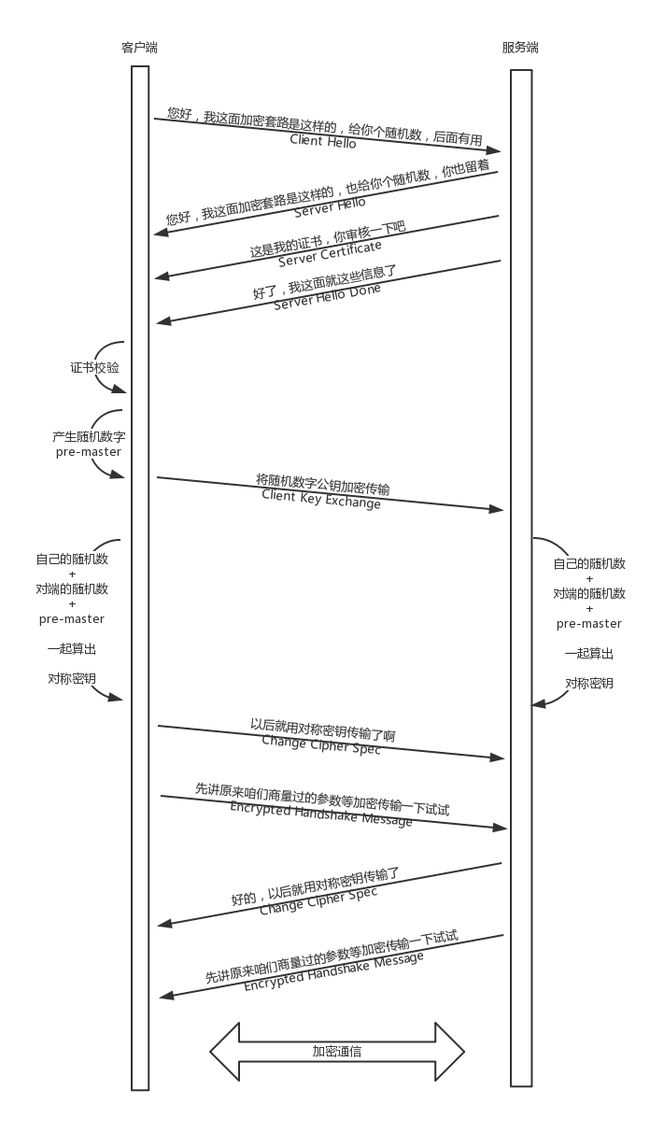
3.HTTPS请求过程

握手过程：

• [明文]客户端发送随机数client_random和支持的加密方式列表
• [明文]服务端发送随机数
• [明文]服务端发送数字证书
• 服务端验证证书
• [公钥加密]服务端产生一个随机数字，并将这个数字使用公钥传输给服务端
• 两端分别通过client_random，server_random和premaster secret生成master secret（对称加密秘钥client_key）

传输数据过程

• 之后就可以根据client_key对信息对称加密和对称解密。

图示：

HTTP的双向认证
上面说的是单向证书认证。
在这种情况下，客户端可以验证服务端的身份，但服务端不能验证客户端的身份。
所以在异乡要求安全性比较高的场景中，使用双向验证，即客户端验证服务端证书，服务端验证客户端证书

4.HTTPS缺点

https的安全性考虑

• HTTPS协议的加密范围也比较有限，在黑客攻击、拒绝服务攻击、服务器劫持等方面几乎起不到什么作用
• SSL证书的信用链体系并不安全，特别是在某些国家可以控制CA根证书的情况下，中间人攻击一样可行

成本考虑

• SSL证书需要购买申请，功能越强大的证书费用越高
• 根据ACM CoNEXT数据显示，使用HTTPS协议会使页面的加载时间延长近50%，增加10%到20%的耗电。
• HTTPS连接缓存不如HTTP高效，流量成本高。
• HTTPS连接服务器端资源占用高很多，支持访客多的网站需要投入更大的成本。
• HTTPS协议握手阶段比较费时，对网站的响应速度有影响，影响用户体验。比较好的方式是采用分而治之，类似12306网站的主页使用HTTP协议，有关于用户信息等方面使用HTTPS。

八.参考资料

RSA 非对称加密原理（小白也能看懂哦~）
b站妈咪说视频《素数6，基于欧拉函数的RAS加密》
哈希(Hash)与加密(Encrypt)的基本原理、区别及工程应用
数字签名和数字证书的原理解读(图文)
HTTPS工作原理
极客时间 趣谈网络协议 https协议：点外卖的过程原来这么复杂