双目立体匹配算法--归一化互相关(NCC)详解和代码实现(python)
原理:
- 对于原始的图像内任意一个像素点 ( p x , p y ) (p_x,p_y) (px,py)构建一个 n × n n\times n n×n的邻域作为匹配窗口。然后对于目标相素位置 ( p x + d , p y ) (p_x+d, p_y) (px+d,py)同样构建一个 n × n n\times n n×n大小的匹配窗口,对两个窗口进行相似度度量,注意这里的 d d d有一个取值范围。对于两幅图像来说,在进行 N C C NCC NCC计算之前要对图像处理,也就是将两帧图像校正到水平位置,即光心处于同一水平线上,此时极线是水平的,否则匹配过程只能在倾斜的极线方向上完成,这将消耗更多的计算资源。
- N C C NCC NCC计算公式如下图所示:

其中 N C C ( p , d ) NCC(p,d) NCC(p,d)得到的值得范围将在 [ − 1 , 1 ] 之 间 [-1,1]之间 [−1,1]之间。
W p W_p Wp为之前提到的匹配窗口。
I 1 ( x , y ) I_1(x,y) I1(x,y)为原始图像的像素值。
I 1 ‾ ( p x , p y ) \overline{I_1}(p_x,p_y) I1(px,py)为原始窗口内像素的均值。
I 2 ( x + d , y ) I_2(x+d,y) I2(x+d,y)为原始图像在目标图像上对应点位置在 x x x方向上偏移 d d d后的像素值。
I 2 ‾ ( p x + d , p y ) \overline{I_2}(p_x+d, p_y) I2(px+d,py)为目标图像匹配窗口像素均值。 - 若 N C C = − 1 NCC = -1 NCC=−1,则表示两个匹配窗口完全不相关,相反,若 N C C = 1 NCC = 1 NCC=1时,表示两个匹配窗口相关程度非常高。
匹配流程
- 采集图像:通过标定好的双目相机采集图像,当然也可以用两个单目相机来组合成双目相机。
- 极线校正:校正的目的是使两帧图像极线处于水平方向,或者说是使两帧图像的光心处于同一水平线上。通过校正极线可以方便后续的 N C C NCC NCC操作。
- 由标定得到的内参中畸变信息中可以对图像去除畸变。
- 通过校正函数校正以后得到相机的矫正变换R和新的投影矩阵P,接下来是要对左右视图进行去畸变,并得到重映射矩阵。
- 特征匹配:这里便是我们利用 N C C NCC NCC做匹配的步骤啦,匹配方法如上所述,右视图中与左视图待测像素同一水平线上相关性最高的即为最优匹配。完成匹配后,我们需要记录其视差d,即待测像素水平方向xl与匹配像素水平方向xr之间的差值 d = x r − x l d = x_r - x_l d=xr−xl,最终我们可以得到一个与原始图像尺寸相同的视差图 D D D。
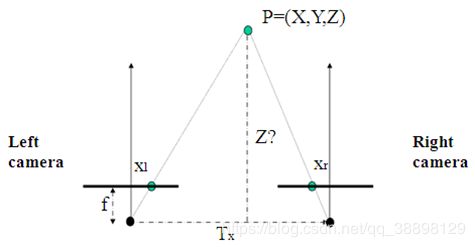
- 深度恢复:通过上述匹配结果得到的视差图 D D D,我们可以很简单的利用相似三角形反推出以左视图为参考系的深度图。计算原理如下图所示:
如图, T x Tx Tx为双目相机基线, f f f为相机焦距,这些可以通过相机标定步骤得到。而 x r − x l xr - xl xr−xl就是视差 d d d。
通过公式 z = z = z= f × T x d {f \times Tx }\over d df×Tx可以很简单地得到以左视图为参考系的深度图了。
至此,我们便完成了双目立体匹配。倘若只是用于图像识别,那么到步骤3时已经可以结束了。
代码实现:
import numpy as np
import cv2
import math
im1 = 'im2.ppm'
im2 = 'im6.ppm'
img1 = cv2.imread(im1, cv2.CV_8UC1)
img2 = cv2.imread(im2, cv2.CV_8UC1)
rows, cols = img1.shape
print(img1.shape)
#用3*3卷积核做均值滤波
def NCC(img1,img2,avg_img1,avg_img2,disparity,NCC_value,deeps, threshold,max_d, min_rows, max_rows):
#设立阈值
ncc_value = threshold
if min_rows == 0:
min_rows += 1
for i in range(3, max_rows - 3):
for j in range(3, cols-3):
if j < cols - max_d-3:
max_d1 = max_d
else:
max_d1 = cols - j - 3
for d in range(4, max_d1):#减一防止越界
ncc1 = 0
ncc2 = 0
ncc3 = 0
for m in range(i-3, i+4):
for n in range(j-3, j+4):
ncc1 += (img2[m, n] - avg_img2[i, j])*(img1[m, n+d]-avg_img1[i, j+d])
ncc2 += (img2[m, n] - avg_img2[i, j])*(img2[m, n] - avg_img2[i, j])
ncc3 += (img1[m, n+d]-avg_img1[i, j+d])*(img1[m, n+d]-avg_img1[i, j+d])
ncc_b = math.sqrt(ncc2*ncc3)
ncc_p_d = 0
if ncc_b != 0:
ncc_p_d = ncc1/(ncc_b)
if ncc_p_d > ncc_value:
ncc_value = ncc_p_d
disparity[i, j] = d
NCC_value[i ,j] = ncc_p_d
ncc_value = threshold
print("iter{0}".format(i))
if __name__ == "__main__":
disparity = np.zeros([rows, cols])
NCC_value = np.zeros([rows, cols])
deeps = np.zeros([rows, cols])
# 用3*3卷积核做均值滤波
avg_img1 = cv2.blur(img1, (7, 7))
avg_img2 = cv2.blur(img2, (7, 7))
img1 = img1.astype(np.float32)
img2 = img2.astype(np.float32)
avg_img1 = avg_img1.astype(np.float32)
NCC(img1,img2,avg_img1,avg_img2, disparity, NCC_value,deeps, 0.6,64,0,150)
disp = cv2.normalize(disparity, disparity, alpha=0, beta=255, norm_type=cv2.NORM_MINMAX,
dtype=cv2.CV_8U)
cv2.imshow("depth", disp)
cv2.waitKey(0) # 等待按键按下
cv2.destroyAllWindows()#清除所有窗口
print(NCC_value)
参考博客:
双目立体匹配——归一化互相关(NCC)