浅谈浮点数的比较
由于计算机中采用的是有限位的二进制编码,所以浮点数在计算机中的存储不总是精确的。例如,在经过大量计算后,一个浮点型的数3.14在计算机中可能就存储成3.140000000001,也有可能存储成3.1499999999999,这种情况下会对比较操作带来极大的干扰,所以我们需要引入一个极小数 eps 来对这种误差进行修正。
1. 等于运算符(==)

如果一个数 a 在 [b-eps, b+eps] 的区间中时,就应当判断为 a==b 成立。经验表明, eps 取 10-8是一个合适的数字——对大多数的情况既不会漏判,也不会误判。因此,我们可以将 eps 定义为常量 1e-8:
const double eps = 1e-8;
为了使比较更加方便,我们可以将比较操作写成宏定义的形式:
#define Equ(a, b) ((fabs((a) - (b))) < (eps))
如果想要使用不等于,只需要在使用时的 Equ 前面加一个非运算符 “ ! ” 即可( ! Equ(a, b))。于是在程序中就可以使用 Equ 函数来对浮点数进行比较了:
#include 对于这个程序,如果写成 db == 1.23 ,会发现同样输出 true。其实像这种比较简单的比较情况下是可以忽视误差的(事实上,如果没有经过容易损失精度的计算,就不需要考虑误差,可以直接比较),但是当一个变量进行了误差较大的运算后,精度的损失就不可忽视了。例如下面的代码中,db1 和 db2 的精确值都应该是 π ,但是却输出了 false ;而使用了 Equ 函数就会输出 true。
#include 显然,由于这种误差影响,其他比较运算符也会出现差错,因此必须进行修正。
2. 大于运算符(>)
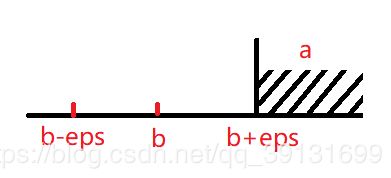
如果一个数 a 要大于 b,那么就必须在误差 eps 的扰动范围之外大于 b ,因此只有大于 b+eps 的数才能判定为大于 b (也即 a 减 b 大于 eps)。
#define More(a, b) (((a) - (b)) > (eps))
3. 小于运算符(<)

与大于运算符类似,如果一个数 a 要小于 b ,那么就必须在误差 eps 的扰动范围之外小于 b ,因此只有小于 b-eps 的数才能判定为小于 b (也即 a 减 b 小于 -eps)。
#define Less(a, b) (((a) - (b)) < (-eps))
4. 大于等于运算符(>=)

由于大于等于运算符可以理解为大雨运算符和等于运算符的结合,于是需要让一个数 a 在误差扰动范围内能够判定其为大于或等于 b ,因此大于 b-eps 的数都应当判定为大于等于 b (也即 a 减 b 大于 -eps)。
#define MoreEqu(a, b) (((a) - (b)) > (-eps))
5. 小于等于运算符(<=)

与大于等于运算符类似,小于等于运算符可以理解为小雨运算符和等于运算符的结合,于是需要让一个数 a 在误差扰动范围内能够判定其为小于或者等于 b ,因此小于 b+eps 的数都应当判定为小于等于 b (也即 a 减 b 小于 eps )。
#define LessEqu(a, b) (((a) - (b)) < (eps))
6. 圆周率π
圆周率 π 不需要死记,因为由 cos(π) = -1 可知 π = arccos(-1)。因此只需要把 π 写成常量 acos(-1.0) 即可。
const double Pi = acos(-1.0)
最后几点:
① 由于精度问题,在经过大量运算后,可能一个变量中存储的0是个很小的负数,这时,如果对其开根号 sqrt ,就会因不在定义域内而出错。同样的问题还出现在 asin(x) 当 x 存放+1、acos(x) 当 x 存放-1 时。这种情况需要用 eps 使变量保证在定义域内。
② 在某些由编译环境产生的原因下,本应为 0.00 的变量在输出时会变成 -0.00 。这个问题是编译环境本身的 bug ,只能把结果存放到字符串中,然后与-0.00进行比较,如果比对成功,则加上 eps 来修正为0.00。