熵通常被认为描述一个系统或者分布的不确定性,熵越大,系统越混乱,不确定性越大。
机器学习与数据挖掘的算法中大量的应用了熵来评价例如结果的多样性、数据分布的纯净度等。
比如在决策树模型中,使用信息熵来确定分割节点,即为了使每次划分后数据分布更纯净。
在推荐多样性模块中,应用贪心法,每次计算加入一个商品后整体推荐商品list的熵,熵越大则推荐多样性越好。
熵的定义:
一个随机变量的概率分布为:
P(X=xi) = pi, i=1,2,3,..,n,即该随机变量可以取n个离散的值,如抛硬币为正反面两个值,P(X=正)=0.5, P(X=反) = 0.5
熵的定义为
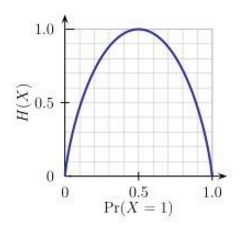
对于二分类问题,熵的概率曲线为:
在伯努利分布中,(1,0) 这种分布熵为0(不确定性最小),(0.5,0.5)这种分布熵最大
条件熵:H(Y|X)
定义为X给定条件下Y的条件概率分布的熵对X的数学期望:
ex1:
小A考试通过与不通过概率的分布为(0.5,0.5),则熵为1 (值为观察上图,没有自己计算)。
加入条件,小A考试前复习与不复习的概率为(0.5,0.5),在复习情况下考试通过的概率分布为(0.8,0.2),在不复习的情况下考试通过的概率分布为(0.2,0.8),则条件熵为(0.5 * 0.7 + 0.5 * 0.7) = 0.7注:H([0.8,0.2])~= 0.7
信息增益定义:
信息增益的定义为:熵-条件熵 ,比如ex1中,信息增益为0.3。
决策树根据信息增益选择分割特征就是通过信息增益。 (决策树ID3算法)即在加入了某特征的约束后,对于label的分布的熵的前后变化即为该特征的信息增益,选择信息增益最大的节点作为决策树该次分割的节点。
信息增益比
信息增益倾向于选择离散取值多的特征,因此引入信息增益比的概念来平衡
信息增益比=信息增益/数据集关于条件特征的值的熵H {D(A)}
数据集关于条件特征的值,即将数据集对特征A(而不是在特征A的条件下对label的类别数计算熵)的熵,显然,特征A的类别数越多,熵就越大,因此作为分母来平衡特征选择(决策树C4.5算法)
相对熵:
相对熵,又称KL散度( Kullback–Leibler divergence),是描述两个概率分布P和Q差异的一种方法。它是非对称的,这意味着D(P||Q) ≠ D(Q||P)。
p(x)与q(x)是两个概率分布,则p对q的相对熵计算如上式。
看公式感觉十分复杂,实际在计算中非常简单。
ex2:
对于两个二分类的概率分布,分布A=(0.5,0.5),分布B=(0.25,0.75)
则相对熵D(A||B) = 0.5 * log(0.5/0.25) + 0.5 * log(0.5/0.75) =0.14
推荐中的应用,多样性模块:
在推荐多样性模块(推荐第三轮排序中),使用贪心算法,每次在排序候选列表(一般设为长度为N的一个窗口)选出一个另前后分布相对熵变化最大的商品进来:
在已有推荐结果的列表里,选择了8个商品,目前已选择商品的分布为 (苹果,帽子,手机,围巾)(1,2,3,2)=> (0.125, 0.25, 0.375, 0.25)
case1:
在候选的列表里有(苹果,帽子,手机),需要添加哪一个?
添加苹果的话,分布变为(2,2,3,2) = (2/9,2/9,1/3,2/9) ,
D(苹果)= 2/9 * log((2/9) / (1/8)) + 2/9 * log(2/9/ (1/4)) + 1/3* log(1/3/(3/8)) + 2/9 * log(2/9/(2/8)) = 0.03624967113471546
添加手机的话,分布变为(1,2,4,2) = (1/9,2/9,4/9,2/9) D(手机) = 0.0100756632111
可见要添加 苹果。
更一般的,在已选择商品列表里,哪个已经出现的次数最小,选择哪一个,则一定相对熵最大。
# 计算多样性模块中的相对熵
import math
def KL_diver(p1,p2):
rela_entropy = 0
for i in range(len(p1)):
rela_entropy += p2[i] * math.log(p2[i] * 1.0 / p1[i])
print (rela_entropy)
p1 = [0.125,0.25,0.375,0.25]
p2 = [2.0/9,2.0/9,3.0/9,2.0/9]
KL_diver(p1,p2)
>> 0.03624967113471546
case2:
在候选的列表里有(苹果,帽子,柚子),需要添加哪一个?
答案是柚子,在相对熵里面,如果一个元素本身没有出现在原分布里,则添加进已选列表分布,相对熵一定最大。
也可以在原分布中赋予没有出现的柚子一个极小的值如0.001,这样再计算相对熵时候log((1/9)/0.001)能得到一个很大的值,自然就能选出之前不存在的柚子。
TD-IDF算法就可以理解为相对熵的应用:词频在整个语料库的分布与词频在具体文档中分布之间的差异性。
交叉熵:
对于真实分布与非真实分布,计算公式为
一个例子
假设对于一条样本,做二分类,真实分布为(1,0) = (y,1-y)模型预测为正类的打分为0.7 =p(sigmoid),则模型预测分布为(0.7,0.3) = (p,1-p),
则交叉熵为1 * log2(1/0.7) + 0 * log2(1/0.3) = 0.356
1 * log2(1/0.7) + 0 * log2(1/0.3) = 1*log2(1) - 1* log2(0.7) + 0 * log2(1) - 0 * log2(0.3) = - (1 * log2(0.7) + 0 * log2(0.3))
更一般的形式
y * log2(1/p) + (1-y) * log2(1/(1-p)) = y* log2(1) - y* log2(p) + (1-y) * log2(1) - (1-y) * log2(1-p)
= - (y * log2(p) + (1-y) * log2(1-p))
观察逻辑回归的对数似然函数:
括号内部对于单条样本的似然函数的值即为对于该条样本,真实分布与非真实分布的交叉熵的负数
因此:最大化似然函数=减少交叉熵(交叉熵越小,与真实分布越接近,交叉熵最小为真实分布的熵,对于二分类,真实分布(1,0)的熵为0)
在逻辑回归里的说法:
最大化对数似然函数 = 最小化损失函数
通常将上式中的对数似然函数取一个符号,作为损失函数,即如下式子:
可见,该式子与上面标红的交叉熵计算公式是一致的。
因此,LR的损失函数又叫做大名鼎鼎的交叉熵损失函数。
总结:
文本总结了机器学习的各种熵,从决策树,到推荐多样性,再到LR的损失函数,是机器学习应用中必备的基础实用知识。