算法（5）：二叉树

终于到傻叉树啦~ 这个是我想好好探讨的一种数据结构，小伙子我觉得它有难度，不管是前中后序以及层级遍历，还是各种递归迭代的妙用，总之，很酷！
加油加油，怎么也得写个十多篇算法系列才行~

目录：
算法：附录
算法（1）：递归
算法（2）：链表
算法（3）：数组
算法（4）：字符串
算法（5）：二叉树
算法（6）：二叉查找树
算法（7）：队列和堆栈（附赠BFS和DFS）
算法（8）：动态规划
算法（9）：哈希表
算法（10）：排序
算法（11）：回溯法
算法（12）：位操作

虽然本系列着重讲算法，但还是需要个引子，所以小编先简单说一下啥是二叉树。二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”（left subtree）和“右子树”（right subtree）。如下图所示，便是一个二叉树结构。

二叉树

既然大家知道什么是二叉树了，那么我们首先来看一下二叉树的前序遍历（Pre-order Traversal）、中序遍历（In-order Traversal）以及后序遍历（Post-order Traversal）。

前序遍历：先根节点，再左节点，最后右节点。（也可以右左根，然后翻转）
中序遍历：先左节点，再根节点，最后右节点。（也可以右根左，然后翻转）
后序遍历：先左节点，在右节点，最后根节点。（也可以根右左，然后翻转）

说白了，就是看遍历根节点的先后顺序。而不论是哪种遍历方法，都是左节点比右节点先遍历。当然，如果按照括号里给出的操作方式，也可以得到相同结果~ 那么，既然知道了如何遍历，根据上面的二叉树图，大家可以写出不同遍历方法的的结果吗？
算了，我也不知道你们会不会，索性先把答案给各位放出来，有兴趣的小伙伴可以先试试自己写，然后和我给的答案对照一下~ ~~蛤？你说你的答案跟我的不一样？那肯定是你错了......~~

前序遍历结果：F B A D C E G I H
中序遍历结果：A B C D E F G H I
后序遍历结果：A C E D B H I G F

既然有这三种遍历方法，那么，它们都有何作用呢？什么时候用前序遍历，什么时候又需要后序遍历呢？大家且听我慢慢道来：

前序遍历：在第一次遍历到节点时就执行操作，一般只是想遍历执行操作（或输出结果）可选用先序遍历，如输出某个文件夹下所有文件与文件夹的名称：遍历文件夹，先输出文件夹名，然后再依次输出该文件夹下的所有文件(包括子文件夹)，如果有子文件夹，则再进入该子文件夹，输出该子文件夹下的所有文件名。这是一个典型的先序遍历过程。
中序遍历：对于二分搜索树，中序遍历的操作顺序（或输出结果顺序）是符合从小到大（或从大到小）顺序的，故要遍历输出排序好的结果需要使用中序遍历。除此之外，还有中缀表达式，一个通用的算术或逻辑公式表示方法。符合人类的逻辑（例：2 + 3）.
后序遍历：后续遍历的特点是执行操作时，肯定已经遍历过该节点的左右子节点。1. 故适用于进行破坏性操作的情况，比如删除节点（因为我们在删除节点时需要先删除左右两子节点，再删除该节点）。2. 其次，如果我们要统计文件夹大小，也需要后序遍历来实现：若要知道某文件夹的大小必须先知道该文件夹下所有文件的大小，如果有子文件夹，若要知道该子文件夹大小，必须先知道子文件夹所有文件的大小。这是一个典型的后序遍历过程。3. 既然有了中缀表达式，那么也有相应的后缀表达式，~~当然也有前缀表达式，~~后缀表达式是一种不需要括号的表达法。符合计算机的逻辑（例：2 3 +）。

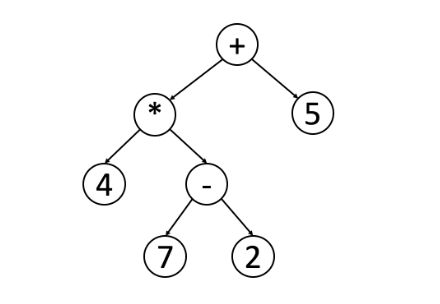
关于中缀和后缀表达式，我愿意再给大家详细说明一下，各位官爷请看下图：

数学表达式

如果我们用中序遍历，那么可以非常迅速的得到 4 * 7 - 2 + 5这么一个式子。但是，每个运算符的优先级，很难写程序去判定。比如，我们想表示 4 * （7 - 2） + 5的式子，即让减号的优先级最高，该如何计算呢？这时，就需要后缀表达式出场了。我们可以得到 4 7 2 - * 5 +这么一串结果。屏幕前的你们可能已经开始认真思考，内心也产生了宝贵的想法： ~~zhe ta ma shen me ji ba wan yi er...~~ 但是计算机可是如获至宝，开心的像个两百斤的孩子一样。因为它可以很轻易的算出结果：建立一个栈（stack，这玩意遵循LIFO，即 last in，first out 原则），不停的将节点值压进栈里，当节点值为运算符时，它便弹出最新压入的值做运算，并将结果再压入栈中。so easy！ ~~哪里不会点哪里，妈妈再也不用担心我的学习啦...~~

洋洋洒洒上千字，没点代码怎么行。

问题1：二叉树前序遍历（Binary Tree Preorder Traversal）
输入：二叉树根节点
输出：[1, 2, 4, 3, 5]

前序遍历比较简单，一边遍历，一边装节点值。以下代码用了非递归方式，大伙可以试试如何用递归写~（递归写起来方便些，但是执行效率会偏低）

class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

def preorderTraversal(root):
    cur_node = root
    stack = []
    res = []

    while stack or cur_node:
        if cur_node:
            res.append(cur_node.val)
            stack.append(cur_node)
            cur_node = cur_node.left
        else:
            cur_node = stack.pop()
            cur_node = cur_node.right
    return res

if __name__ == '__main__':
    node = head = TreeNode(1)
    node.left =  TreeNode(2)
    node.right = TreeNode(3)
    node.left.right = TreeNode(4)
    node.right.left = TreeNode(5)

    ans = preorderTraversal(head)
    print(ans)

问题2：二叉树中序遍历（Binary Tree Inorder Traversal）
输入：同上
输出：[2, 4, 1, 5, 3]

class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

def inorderTraversal(root: TreeNode) -> list:
    cur_node = root
    stack = []
    res = []

    while stack or cur_node:
        if cur_node:
            stack.append(cur_node)
            cur_node = cur_node.left
        else:
            cur_node = stack.pop()
            res.append(cur_node.val)
            cur_node = cur_node.right
    return res

if __name__ == '__main__':
    node = head = TreeNode(1)
    node.left =  TreeNode(2)
    node.right = TreeNode(3)
    node.left.right = TreeNode(4)
    node.right.left = TreeNode(5)

    ans = inorderTraversal(head)
    print(ans)

问题3：二叉树后序遍历（Binary Tree Postorder Traversal）
输入：同上
输出：[4, 2, 5, 3, 1]
后序遍历的话运用了倒装方式，先装节点值，再装右节点，最后装左节点。返回结果时将列表翻转即为答案。

class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

def postorderTraversal(root: TreeNode) ->list:
    cur_node = root
    stack = []
    res = []

    while stack or cur_node:
        if cur_node:
            stack.append(cur_node)
            res.append(cur_node.val)
            cur_node = cur_node.right
        else:
            cur_node = stack.pop()
            cur_node = cur_node.left
    return res[::-1]

if __name__ == '__main__':
    node = head = TreeNode(1)
    node.left =  TreeNode(2)
    node.right = TreeNode(3)
    node.left.right = TreeNode(4)
    node.right.left = TreeNode(5)

    ans = postorderTraversal(head)
    print(ans)

问题4：二叉树逐层遍历（Binary Tree Level Order Traversal）。这里是将二叉树一层一层，从左往右遍历，用到了广度优先搜索（Breadth-First Search）的思想。
输入：同上
输出：[[1], [2, 3], [4, 5]]

class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None


def levelOrder(root: TreeNode) -> list:
    if root == None: return []
    queue = [[root]]
    res = []
    while queue:
        curlevel = queue.pop()
        newlevel = []
        val = []
        for node in curlevel:
            if node:
                val.append(node.val)
                newlevel.append(node.left)
                newlevel.append(node.right)
        if newlevel != []:
            queue.append(newlevel)
        if val != []:
            res.append(val)
    return res

if __name__ == '__main__':
    node = head = TreeNode(1)
    node.left =  TreeNode(2)
    node.right = TreeNode(3)
    node.left.right = TreeNode(4)
    node.right.left = TreeNode(5)

    ans = levelOrder(head)
    print(ans)

问题5：判断一个二叉树是否为对称二叉树。
输入：二叉树，如下所示：
输出：True

代码如下（就我个人理解，应该是属于自顶向下的递归法，如果不满足先决条件的话，将不再继续递归，直接返回False结果）：

class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

def isSymmetric(root: TreeNode) -> bool:
    def helper(left, right):
        if not left and not right: return True
        if left and right and left.val == right.val:
            return helper(left.right, right.left) and helper(left.left, right.right)
        return False

    if not root: return True
    return helper(root.left, root.right)

if __name__ == '__main__':
    node = head = TreeNode(1)
    node.left =  TreeNode(2)
    node.right = TreeNode(2)
    node.left.right = TreeNode(3)
    node.right.left = TreeNode(3)

    ans = isSymmetric(head)
    print(ans)

自顶向下（top-down）和自底向上（bottom-up）的递归方法

自顶向下：在每次递归调用时，我们利用该节点的信息计算出某些值，然后通过递归调用将这些值（这些传递的值一般是全局变量）传递给它的子节点，一直到叶子节点。
自底向上：在使用递归法时，我们先对子节点使用递归函数，然后让子节点返回一些值（这时一般就不传递全局变量），最后我们利用子节点返回的值进行计算。

举个小小例子：计算某个二叉树的深度。（如果是屏幕面前的你，你会如何计算呢？~~感觉自己讲话方式好 zhi zhang，，，~~）

如果是自顶向下（此时从上往下树的深度执行加一操作)：

1. return if root is null
2. if root is a leaf node:
3.      answer = max(answer, depth)         // update the answer if needed
4. maximum_depth(root.left, depth + 1)      // call the function recursively for left child
5. maximum_depth(root.right, depth + 1)     // call the function recursively for right child

这个时候你又想自底向上了（这时是从下往上深度不停加一）：

1. return 0 if root is null                 // return 0 for null node
2. left_depth = maximum_depth(root.left)
3. right_depth = maximum_depth(root.right)
4. return max(left_depth, right_depth) + 1  // return depth of the subtree rooted at root

大家可以看出，如果我们可以得到该节点的信息（如节点深度为前面总共深度再加一），并且这些信息可以帮助到子节点的计算，那么就可以考虑自顶向下法；如果我们知道子节点的结果，并通过它来计算该节点的结果，那么便可以使用自底向上法。总而言之一句话，这玩意不简单呐。

例题6：欢迎大家收看例题没完没了系列之路径求和(Path Sum)。给定一颗二叉树，如果从根节点到某个叶子节点这条路径上的值之和等于目标值’target‘，则返回True，否则返回False。
输入：见例题1
输出：True（1+2+4=7），False，True（1+3+5=9）
这个代码属于自顶向下方法：

class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

def hasPathSum(root: TreeNode, target: int) -> bool:
    def helper(node, ans):
        if not node: return False
        if not node.left and not node.right: return ans + node.val == target
        return helper(node.left, ans + node.val) or helper(node.right, ans + node.val)

    return helper(root, 0)

if __name__ == '__main__':
    node = head = TreeNode(1)
    node.left =  TreeNode(2)
    node.right = TreeNode(3)
    node.left.right = TreeNode(4)
    node.right.left = TreeNode(5)

    for i in range(7,10):
        print(hasPathSum(head,i))

例题7：根据中序遍历和后序遍历的列表，构建该二叉树。
输入：inorder = [9,3,15,20,7]，postorder = [9,15,7,20,3]
输出：二叉树，如下所示。

对于一棵树的中序遍历，根节点肯定处于遍历结果的中间（假设这棵树有左子树），后序遍历的时候根节点肯定是最后一个遍历的元素。所以我们在后序遍历列表当中，依次从最后位置取出根节点，并且找到该根节点在中序遍历列表当中的位置。此时，该位置左边就是这棵树的左子树元素，右边元素就是这棵树的右子树元素。如此递归下去，便可得到想要结果~
大家可以思考一个问题，那就是根据中序遍历和前序遍历是否也可以构建出唯一的二叉树？（答案是可以，做法也是几乎一样，在前序遍历列表当中从前往后取根节点就可以~）那么前序和后序遍历能构建唯一的一棵二叉树吗？（答案是不行，因为你无法判断节点属于左子树还是右子树）

class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

def buildTree( inorder: list, postorder: list) ->TreeNode:
    if not inorder or not postorder: return
    val = postorder.pop()
    node = TreeNode(val)
    idx = inorder.index(val)

    node.right = buildTree(inorder[idx + 1:], postorder)
    node.left = buildTree(inorder[:idx], postorder)

    return node

def preorder(head):
    def helper(node,ans):
        if not node:return
        ans.append(node.val)
        helper(node.left,ans)
        helper(node.right,ans)

    ans =[]
    helper(head,ans)
    return ans

if __name__ == '__main__':
    inorder = [9, 3, 15, 20, 7]
    postorder = [9, 15, 7, 20, 3]
    head = buildTree(inorder,postorder)

    ans = preorder(head)
    print(ans)

例题8：输入两棵二叉树A，B，判断B是不是A的子结构。（ps：我们约定空树不是任意一个树的子结构）
输入：A

输入：B

    20
   /  \
  15   7

输出：True

class Solution:
    def HasSubtree(self, pRoot1, pRoot2):
        # write code here
        if not pRoot1 or not pRoot2:
            return False
        return self.is_subtree(pRoot1, pRoot2) or self.HasSubtree(pRoot1.left, pRoot2) or self.HasSubtree(pRoot1.right, pRoot2)
      
    def is_subtree(self, A, B):
        if not B:
            return True
        if not A or A.val != B.val:
            return False
        return self.is_subtree(A.left,B.left) and self.is_subtree(A.right, B.right)

求求求求求，点赞和关注！

算法（5）：二叉树

你可能感兴趣的:(算法（5）：二叉树)