在做leetcode的时候,遇到hard题大家往往都觉得头疼,但其实,掌握方法,举一反三,hard题有时候我们也能想到好的思路,顺利攻破,今天我们就介绍一下动态规划在字符串匹配中的应用,相同类型的题目在前120道题中居然出现了4次!有必要好好总结一下!
这四道题分别是:
10. Regular Expression Matching:https://leetcode.com/problems/regular-expression-matching/description.
44.Wildcard Matching:https://leetcode.com/problems/wildcard-matching/description/
97. Interleaving String:https://leetcode.com/problems/interleaving-string/description/
115. Distinct Subsequences:https://leetcode.com/problems/distinct-subsequences/description/
上面四道题都是hard难度的题,但是存在一定的共性,都是判断两个字符串是否匹配或者两个字符串和第三个字符串时候匹配的问题,像这样的问题,我们如果使用回溯法的话,时间复杂度太高, 有时可能会超过时间限制,但是使用动态规划的方法,可以极大的缩小时间复杂度,达到时间要求。下面,我们一道题一道题来讲解,希望大家可以发现其中的共性,举一反三,以后遇到类似的问题,可以得心应手。
10. Regular Expression Matching
首先,我们来看一下题目的要求:
这一题要求是判断后一个字符串是否和前面的字符串是匹配的,即实现一个简单的正则匹配,在pattern字符串中,可能会出现两个字符,一个是.这代表任意一个字符,另一个是'*'这代表0个或者多个它前面指向的字符。
动态规划的思路就是找到一个递推的公式,由前往后或者由后往前来求解题目,在字符串匹配问题中,我们的基本的思想就是从前面开始,维护两个指针,一个指针从前往后遍历目标字符串,一个指针从前往后遍历pattern字符串,并不断判断当前两个指针前面的子串是否匹配。这个思想,很容易转换成一张二维表格。我们要做的,就是找到这张二维表格的转换关系或者说递推公式。
那么这张二维表格长什么样子呢?假设我们的的目标字符串是aaaa,pattern字符串是a*b*,那么我们的二维表格如下:
在这张二维表格中,行数是pattern字符串长度+1,而列数是目标字符串长度+1。假设表格叫dp,那么dp[j][i]表示,pattern字符串的子串(0,j)是否和目标字符串的子串(0,i)匹配。如果匹配,该位置就是1,如果不匹配,该位置就是0,那么我们最后的返回结果就是右下角位置的数字。
好了,问题的关键变成了找到表格中0和1的传递关系。我们知道,'.'代表的一个字符,'*'和前面一个字符可以表示任意长度的字符串,当遇到'*'我们如何传递1和0就变成了问题的关键。
我们首先完善表格的第一行和第一列,第一行表示的是,pattern为空字符串时,能和目标字符串的哪些子串匹配,显然除[0][0]外其他都不能匹配。第一列表示的是,当目标字符串为空串时,pattern的哪些子串可以与之匹配,显然pattern只有时空串或者是x*y*这种形式的才可以,即:
arr[0][0] = true;
//第一行剩余元素全部变为false,因为pattern如果是空串,那么只要s不是空串,都不能匹配
for(int i=1;i<=col;i++)
arr[0][i] = false;
//初始化第0列,此时s是空串,所以只能是x*y*这种形式的
//注意,j-1代表的真实的p的索引
for(int j=1;j<=row;j++)
arr[j][0] = (j>1) && (p.charAt(j-1)=='*') && arr[j-2][0];
那剩下的部分如何填充呢,很显然需要一个两层的循环。每次更新一行的值。即每次pattern字符串往下走一个字符,和所有的目标字符串子串进行匹配。接下来需要分两种情况讨论:
假设当前位置是dp[j][i],当遇到'*‘时,'*'的用法无非就两种,代表空串或者代表一个或多个前一个字符。想要dp[j][i]为1,需要满足下面两个条件中的任意一个:
1、dp[j-2][i] = 1,此时'*'代表空串
2、dp[j][i-1] = 1 且 pattern字符串j-2位置的字符和目标字符串i-1位置的字符相同(因为0位置表示了空串,所以数组中i位置代表的是字符串中的i-1位置)或者说pattern字符串j-2位置的字符为'.',此时'*'表示对前一个字符的复制。
如果两个条件都不满足,则dp[j][i]为0
即:
if(p.charAt(j-1)=='*')
arr[j][i] = arr[j-2][i] || (p.charAt(j-2)==s.charAt(i-1) || p.charAt(j-2)=='.') && arr[j][i-1];
那如果遇到的不是*时,问题就很简单了,要么pattern字符串j-1位置的字符为'.',要么二者在该位置的字符相同。当然,还要判断前面的是否匹配,即dp[j-1][i-1]的值。
arr[j][i] = (p.charAt(j-1)=='.' || p.charAt(j-1)==s.charAt(i-1)) && arr[j-1][i-1];
好啦,图片也很明显的表明了数组中0和1的传递规律,仔细想想其实不难呢,嘻嘻。完整的代码如下。
class Solution {
public boolean isMatch(String s, String p) {
int col = s.length();
int row = p.length();
//建立一个boolean数组,数组长度为 row + 1 * col + 1,多的一列一行代表空串的情况
boolean[][] arr = new boolean[row+1][col+1];
arr[0][0] = true;
//第一行剩余元素全部变为false,因为pattern如果是空串,那么只要s不是空串,都不能匹配
for(int i=1;i<=col;i++)
arr[0][i] = false;
//初始化第0列,此时s是空串,所以只能是x*y*这种形式的
//注意,j-1代表的真实的p的索引
for(int j=1;j<=row;j++)
arr[j][0] = (j>1) && (p.charAt(j-1)=='*') && arr[j-2][0];
//主体循环开始
for(int i=1;i<=col;i++){
for(int j=1;j<=row;j++){
//如果当前的pattern字符串是*,需要同时满足下面的两个条件,才能为true,此时s其实是固定住的,在思考的时候可以这么想
//1、如果往前数两行的位置可以匹配,那么这里的*可以代表空,此时可以匹配,
//如果s是aa,p是a*的话,我们不能根据往前数两行来判断,这时必须满足p[j-2]==s[i-1] 或者说 p[j-2]是'.'
//
if(p.charAt(j-1)=='*')
arr[j][i] = arr[j-2][i] || (p.charAt(j-2)==s.charAt(i-1) || p.charAt(j-2)=='.') && arr[j][i-1];
else
arr[j][i] = (p.charAt(j-1)=='.' || p.charAt(j-1)==s.charAt(i-1)) && arr[j-1][i-1];
}
}
return arr[row][col];
}
}
44. Wildcard Matching
44题的题目描述如下:
这道题和10题的思路大致是一样的,甚至比第10题更简单,因为*可以表示任意长度的字符串,且字符内容不受限制,我们还是要维护一张二维的表格,找到0和1的传递规律。
当遇到'*'时,要么'*'当作空字符串使用,此时dp[j][i] = dp[j-1][i],要么当作一个任意字符,此时dp[j][i] = dp[j][i-1]。
这里就不详细介绍了,具体看下代码大家就明白啦。
class Solution {
public boolean isMatch(String s, String p) {
int row = p.length() + 1;
int col = s.length() + 1;
boolean[][] dp = new boolean[row][col];
dp[0][0] = true;
for(int i=1;i97. Interleaving String
97题的描述如下:
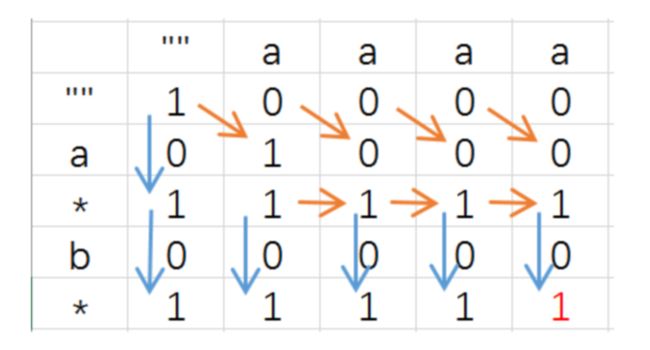
这道题的意思是,判断通过s1和s2的拼接是否可以得到s3,s1和s2中的字符可以穿插使用。s1, s2只有两个字符串,因此可以展平为一个二维地图,使用动态规划的思路,判断是否能从左上角走到右下角。
当s1到达第i个元素,s2到达第j个元素:
地图上往右一步就是s2[j-1]匹配s3[i+j-1]。
地图上往下一步就是s1[i-1]匹配s3[i+j-1]。
示例:s1="aa",s2="ab",s3="aaba"。标1的为可行。最终返回右下角。
class Solution {
public boolean isInterleave(String s1, String s2, String s3) {
if(s1.length() + s2.length() != s3.length())
return false;
boolean[][] arr = new boolean[s1.length()+1][s2.length()+1];
arr[0][0] = true;
for(int i=1;i115. Distinct Subsequences
115题的题目描述如下:
这道题不是求两个字符串是匹配,而是判断S有多少种方式可以得到T。但其实还是动态规划,我们一个定义二维数组dp,dp[i][j]为字符串s(0,i)变换到t(0,j)的变换方法的个数。
如果S[i]==T[j],那么dp[i][j] = dp[i-1][j-1] + dp[i-1][j]。意思是:如果当前S[i]==T[j],那么当前这个字符即可以保留也可以抛弃,所以变换方法等于保留这个字符的变换方法加上不用这个字符的变换方法, dp[i-1][j-1]为保留这个字符时的变换方法个数,dp[i-1][j]表示抛弃这个字符时的变换方法个数。
如果S[i]!=T[i],那么dp[i][j] = dp[i-1][j],意思是如果当前字符不等,那么就只能抛弃当前这个字符。
class Solution {
public int numDistinct(String s, String t) {
int[][] res = new int[s.length()+1][t.length()+1];
res[0][0] = 1;
for(int i=1;i以上就是目前遇到的4道通过动态规划求解字符串匹配的经典问题,我们都是通过维护一个二维表格的方式来得到最终的答案,问题的关键就是得到表格中相邻元素的递推关系,这需要结合实际的问题来进行具体分析。