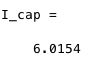随机模拟-Monte Carlo积分及采样（详述直接采样、接受-拒绝采样、重要性采样）

转载请注明出处 http://www.jianshu.com/p/3d30070932a8
作者：@贰拾贰画生

---

1. Monte Carlo 积分

蒙特卡洛方法的思想很简单，就是用随机投点法来模拟不规则图形的面积。
比如在1*1的矩形中，有一个不规则的图形，我们想要直接计算该图形的面积很困难，那怎么办呢？我们可以拿N个点，随机抛在1*1的矩形框中，数一下落入该不规则图形中的点的个数count，那么该不规则图形的面积就可以用count/N近似。

除了求面积，蒙特卡洛方法还有什么应用呢？

求积分。

有函数f(x)，它在区间[0, a]的积分就是x=0, x=a以及f(x)和x轴围成区域的面积，我们将[0, a]划分n份，那么积分可以写成：

我们采用蒙特卡洛采样的思想，右边把极限去掉，只取n个点，那么剩下的部分岂不就是f(x)的均值E[f(x)]？没错，就是n个点的f(x)的均值。

所以，对于f(x)在[a, b]的积分，我们可以通过求f(x)的均值来模拟。

举个小例子，我们求这个积分：

我们随机取[0,1]上的N个点，然后求其均值就是模拟该积分。
MATLAB代码

N_samples = 100000;
f_N = zeros(N_samples, 1);
Z_N = rand(N_samples, 1);
 
for i = 1 : N_samples
    f_N (i, 1) = atan(Z_N(i, 1)) / (Z_N(i, 1) * Z_N(i, 1) + Z_N(i, 1) * sin(Z_N(i, 1)));
end
 
I_cap = mean(f_N)

Z_N保存随机取的N_samples = 100000个点的x值，f_N保存f(x)，然后求f_N的均值，得到的就是积分I。

2. 直接采样

直接采样的思想是，通过对均匀分布采样，实现对任意分布的采样。因为均匀分布采样好猜，我们想要的分布采样不好采，那就采取一定的策略通过简单采取求复杂采样。
假设y服从某项分布p(y)，其累积分布函数CDF为h(y)，有样本z~Uniform(0,1)，我们令 z = h(y)，即 y = h(z)^(-1)，结果y即为对分布p(y)的采样。

直接采样

举个例子：

直接采样有一个问题，就是上图下方的那两个问号。

3. 接收-拒绝采样

接受-拒绝采样的思想是，对于分布p(z)，很难通过直接采样进行采样，但是我们有q(z)，可以通过直接采样或其他采样进行采样，那么我们怎么可以通过q(z)采样得到p(z)的采样呢？
先看下图：

接收-拒绝采样

红色的是p(z), 蓝色的是q(z)，我们对q(z)乘一个参数k，让k能正好包住p(z)，那么对于每一个从q(z)得到的样本z0，我们有一定的概率接受它，概率的大小就是p(z0) / kq(z0)。很容易就能看出来，在p(z)和kq(z)相切的地方的采样，接受率就是1。那么有人问了，接受率能计算出来，但是我们对于一个样本z0，到底怎么判断是接受还是不接受啊？我们有u~Uniform[0,1]，对于每一个样本z0，我们一个u0，如果u0 <= p(z0) / kq(z0)，我们就接受，否则就拒绝。重复此过程，得到的样本就服从分布p(z)。

接受-拒绝采样算法

当然，q(z)的选取要有一定规则：q(z)与p(z)外形要相近，q(z)采样方便。

现在有一个问题，k怎么求？

其实也很简单，看图有 kq(z) >= p(z)，那么k >= p(z) / q(z)，我们求p(z) / q(z)的最大值，即为k。

举个例子，对截断正态分布的接受-拒绝采样。
截断正态分布的意思就是对于正态分布N(a, b) x属于[0, 4]，其在[0, 4]上的积分为1，而不是在负无穷到正无穷的积分为1。截断正态分布不是正态分布，所以，我们知道截断正态分布的概率密度函数。

维基上对截断正态分布的定义：

截断正态分布

分子的小fai是标准正态分布的概率密度函数，分母上的大fai是标准正态分布的累积分布函数。

我们有p(z)服从N(1, 1)， I(0 <= x <= 4)，令q(z)~U[0, 4]，根据上图的公式，p(z)就有了，q(z) = 1/4，所以k = max(p(z) / q(z))，在z = 1（均值）的时候p(z) / q(z)取最大，所以得到k：

这个例子比较巧，分母没有z，我们可以直接判断在z=1时，p(z)/q(z)取最大，如果p(z), q(z)都有z，那么要通过求导的方式求k了。

4. 重要性采样求均值

对于重要性采样，我之前是有个疑问的，既然是采样，为何最后没有得到样本，反而去求均值去了？其他很多介绍重要性采样的文章都没有讲明白这一点，其实重要性采样与接受-拒绝采样有异曲同工之妙。接受拒绝采样时通过接受拒绝的方式对通过q(z)得到的样本进行筛选使得最后得到的样本服从分布p(z)，每个接受的样本没有高低贵贱之分，一视同仁。而重要性采样的思想是，对于通过q(z)得到的样本，我全部接受！全部接受的话会有一个问题，那就是最后样本点分布不能服从p(z)分布，为了矫正这个样本全部接受带来的偏差，我们给每个样本附一个重要性权重，比如，对于p(z0)/q(z0)=1的样本，给的权重大一点，p(z0)/q(z0)=0.1的样本，权重小一点。但是这个权重怎么算呢？哎，我们发现这个p(z0)/q(z0)不就是一个很好的权重标识吗？

重要性采样取得到的是带有重要性权重的服从q(z)分布的样本，这个权重乘以样本之后的结果其实就是服从p(z)分布的。对于这种比较特殊的样本，我们怎么用呢？我们一般用来求均值，所以，这一小节的标题是重要性采样求均值。如果只写重要性采样容易让人产生误解。

重要性采样

应当注意的是，图中p(z)与f(z)的关系，p(z)是一种分布，是相对于z轴的采样点而言的，比如在红色的两个驼峰处，z的取点比较多，在其他地方z的取点就比较少，这叫样本分布服从p(z)。对于f(z)是一种映射关系，将z值映射到其他维度。比如我们熟悉的y = f(x)，将x映射到y。我们所说的求均值就是求f(z)的均值。这一点一定要想明白。

5. 马尔科夫蒙特卡洛采样 & Gibbs采样

这两部分，很多人已经写了不错的文章，我就不写了。
推荐一个博文MCMC(Markov Chain Monte Carlo) and Gibbs Sampling，介绍的已经很清楚了。