傅里叶变换 一维和二维快速傅里叶变换（代码和性能的优化）

1、介绍。

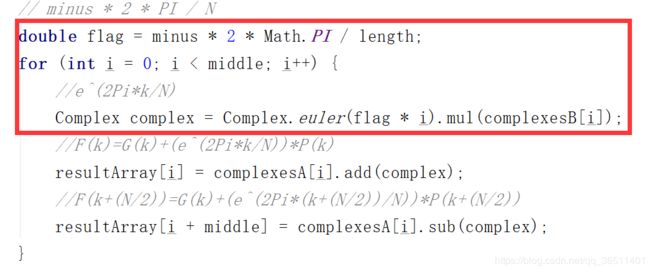
        在类FourierUtils的fftProgress方法中，有这个代码段，我们可以将Complext.euler(flag * i)提前计算好，设置大小为2次幂N，如果没有的话，也要调节到2次幂N。我们设置大小为N,求得复数数组，前半部分存储给FFT使用的，后半部分给IFFT使用。

2、其中复数类和工具类代码不变。可以直接使用文章傅里叶变换 二维快速傅里叶变换（快速的二维离散傅里叶变换、分治法）的复数类和工具类代码。

3、FourierUtils类（只粘贴修改的部分）

package com.zxj.reptile.utils.image;

import com.zxj.reptile.utils.number.Complex;
import com.zxj.reptile.utils.number.NumberUtils;

public class FourierUtils {

    /**
     * 一维快速傅里叶变换FFT  当N不是2次幂时，自动补0
     *
     * @param array 一维数组
     */
    public static Complex[] getFft(double[] array, Complex[] eulerComplexArray) {
        //实际的长度
        int length = array.length;
        //调节过的长度
        int variableLength = eulerComplexArray.length;
        Complex[] variableArray = new Complex[variableLength];
        for (int i = 0; i < variableLength; i++) {
            if (i < length) {
                variableArray[i] = new Complex(array[i]);
            } else {
                variableArray[i] = new Complex();
            }
        }
        return fftProgress(variableArray, 0, eulerComplexArray);
    }

    /**
     * 一维逆快速傅里叶变换IFFT  将结果超过realLength的全部移除
     *
     * @param complexArray 一维复数数组
     * @param realLength   返回的数组长度
     */
    public static double[] getInverseFft(Complex[] complexArray, Complex[] eulerComplexArray, int realLength) {
        int length = complexArray.length;
        Complex[] resultArrays = fftProgress(complexArray, eulerComplexArray.length / 2, eulerComplexArray);
        double[] array = new double[realLength];
        //每个数都要除以N
        for (int i = 0; i < realLength; i++) {
            array[i] = NumberUtils.getRound(resultArrays[i].getReal() / length, 2);
        }
        return array;
    }

    /**
     * 一维快速傅里叶变换FFT和一维逆快速傅里叶变换IFFT递归过程
     *
     * @param complexArray      一维复数数组
     * @param offset            FFT为0，IFFT为N/2
     * @param eulerComplexArray 欧拉数组
     */
    private static Complex[] fftProgress(Complex[] complexArray, int offset, Complex[] eulerComplexArray) {
        int length = complexArray.length;
        if (length == 2) {
            //F(0)=f(0)+f(1),F(1)=f(0)-f(1)
            return new Complex[]{
                    complexArray[0].add(complexArray[1]),
                    complexArray[0].sub(complexArray[1]),};
        } else if (length == 1) {
            return complexArray;
        }
        int middle = length / 2;
        //
        Complex[] a = new Complex[middle];//a(x)=f(2x)
        Complex[] b = new Complex[middle];//b(x)=f(2x+1)
        for (int i = 0; i < middle; i++) {
            a[i] = complexArray[2 * i];
            b[i] = complexArray[2 * i + 1];
        }
        //
        Complex[] complexesA = fftProgress(a, offset, eulerComplexArray);//计算G(k)
        Complex[] complexesB = fftProgress(b, offset, eulerComplexArray);//计算P(k)
        Complex[] resultArray = new Complex[length];//F(k)
        int multiple = eulerComplexArray.length / length;
        for (int i = 0; i < middle; i++) {
            //e^(2Pi*k/N)
            Complex complex = eulerComplexArray[multiple * i + offset].mul(complexesB[i]);
            //F(k)=G(k)+(e^(2Pi*k/N))*P(k)
            resultArray[i] = complexesA[i].add(complex);
            //F(k+(N/2))=G(k)+(e^(2Pi*(k+(N/2))/N))*P(k+(N/2))
            resultArray[i + middle] = complexesA[i].sub(complex);
        }
        return resultArray;
    }

    /**
     * 二维快速傅里叶变换FFT  当N不是2次幂时，自动补0
     *
     * @param arrays 二维数组
     */
    public static Complex[][] getFft(double[][] arrays, Complex[] eulerComplexArray) {
        //实际的行列
        int row = arrays.length;
        int column = arrays[0].length;
        //调节过的长度
        int variableLength = eulerComplexArray.length;
        Complex[][] complexArrays = new Complex[variableLength][variableLength];
        for (int i = 0; i < variableLength; i++) {
            for (int j = 0; j < variableLength; j++) {
                if (i < row && j < column) {
                    complexArrays[i][j] = new Complex(arrays[i][j]);
                } else {
                    complexArrays[i][j] = new Complex();
                }
            }
        }
        return fftProgress(complexArrays, 0, eulerComplexArray);
    }

    /**
     * 二维逆快速傅里叶变换IFFT  将结果行列分别超过realRow和realColumn的全部移除
     *
     * @param complexArrays 二维复数数组
     */
    public static double[][] getInverseFft(Complex[][] complexArrays, Complex[] eulerComplexArray, int realRow, int realColumn) {
        int size = complexArrays.length * complexArrays[0].length;
        complexArrays = fftProgress(complexArrays, eulerComplexArray.length / 2, eulerComplexArray);
        double[][] arrays = new double[realRow][realColumn];
        //每个数
        for (int i = 0; i < realRow; i++) {
            for (int j = 0; j < realColumn; j++) {
                arrays[i][j] = NumberUtils.getRound(complexArrays[i][j].getReal() / size, 2);
            }
        }
        return arrays;
    }

    /**
     * 二维快速傅里叶变换DFT和二维逆快速傅里叶变换IDFT处理过程
     *
     * @param complexArrays     二维复数数组
     * @param offset            FFT为0，IFFT为N/2
     * @param eulerComplexArray 欧拉数组
     */
    private static Complex[][] fftProgress(Complex[][] complexArrays, int offset, Complex[] eulerComplexArray) {
        int length = complexArrays.length;
        //对每行进行一维DFT
        for (int i = 0; i < length; i++) {
            complexArrays[i] = fftProgress(complexArrays[i], offset, eulerComplexArray);
        }
        //倒置，即行和列互换
        complexArrays = Complex.transform(complexArrays);
        length = complexArrays.length;
        //对每行进行一维DFT，实际上是对没倒置前数组的列做一维DFT
        for (int i = 0; i < length; i++) {
            complexArrays[i] = fftProgress(complexArrays[i], offset, eulerComplexArray);
        }
        //倒置回来
        complexArrays = Complex.transform(complexArrays);
        return complexArrays;
    }

    /**
     * 提前生成要用到的关于欧拉计算的数组，因为考虑过将大小调节到2的幂，所以只适合FFT
     *
     * @param length 数组大小
     */
    public static Complex[] getEulerComplex(int length) {
        //调节过的长度
        int variableLength = (int) NumberUtils.getVariablePow(length, 2);
        int middle = variableLength / 2;
        double flag = 2 * Math.PI / variableLength;//2Pi / N
        Complex[] eulerComplexArray = new Complex[variableLength];
        for (int i = 0; i < middle; i++) {
            double angle = flag * i;
            //- 2PI * k / N  给FFT使用
            eulerComplexArray[i] = Complex.euler(-angle);
            //2 * PI * k / N 给IFFT使用
            eulerComplexArray[i + middle] = Complex.euler(angle);
        }
        return eulerComplexArray;
    }
}

4、主要流程代码。

package com.zxj.reptile.test.image;

import com.zxj.reptile.utils.image.FourierUtils;
import com.zxj.reptile.utils.number.ArrayUtils;
import com.zxj.reptile.utils.number.Complex;

import java.util.Arrays;

public class FourierTest {
    public static void main(String[] args) {
        System.out.println("------开始------");
        testDft(1000000);//一维离散傅里叶变换
//        testDft(900, 800);//二维离散傅里叶变换
        System.out.println("------结束------");
    }

    private static void testDft(int row, int column) {
        long time;
        System.out.println("原数据: ");
        double[][] arrays = ArrayUtils.getRandom(row, column, 0, 255);
        System.out.println(String.format("大小为%d行%d列", row, column));
        System.out.println();
        //
        time = System.currentTimeMillis();
        Complex[] eulerComplexArray = FourierUtils.getEulerComplex(row > column ? row : column);
        System.out.println("生成关于欧拉计算的数组花费时间 ：" + (System.currentTimeMillis() - time));
        System.out.println();
        //
        System.out.println("二维快速傅里叶变换FFT: ");
        time = System.currentTimeMillis();
        Complex[][] fftArrays = FourierUtils.getFft(arrays, eulerComplexArray);
        System.out.println("花费时间 ：" + (System.currentTimeMillis() - time));
        System.out.println();
        //
        System.out.println("二维逆快速傅里叶变换IFFT: ");
        time = System.currentTimeMillis();
        double[][] inverseFftArrays = FourierUtils.getInverseFft(fftArrays, eulerComplexArray, row, column);
        System.out.println("花费时间 ：" + (System.currentTimeMillis() - time));
        if (ArrayUtils.equals(arrays, inverseFftArrays)) {
            System.out.println("FFT变换成功");
        } else {
            System.out.println("FFT变换失败");
        }
        System.out.println();
    }

    private static void testDft(int length) {
        long time;
        System.out.println("原数据: ");
        System.out.println(String.format("大小为%d", length));
        double[] array = ArrayUtils.getRandom(length, 0, 255);
        System.out.println();
        //
        time = System.currentTimeMillis();
        Complex[] eulerComplexArray = FourierUtils.getEulerComplex(length);
        System.out.println("生成关于欧拉计算的数组花费时间 ：" + (System.currentTimeMillis() - time));
        System.out.println();
        //
        System.out.println("一维快速傅里叶变换FFT: ");
        time = System.currentTimeMillis();
        Complex[] fftArray = FourierUtils.getFft(array, eulerComplexArray);
        System.out.println("花费时间 ：" + (System.currentTimeMillis() - time));
        System.out.println();
        //
        System.out.println("一维逆快速傅里叶变换IFFT: ");
        time = System.currentTimeMillis();
        double[] inverseFFTArray = FourierUtils.getInverseFft(fftArray, eulerComplexArray, array.length);
        System.out.println("花费时间 ：" + (System.currentTimeMillis() - time));
        if (Arrays.equals(array, inverseFFTArray)) {
            System.out.println("IFFT成功");
        } else {
            System.out.println("IFFT失败");
        }
        System.out.println();
    }
}

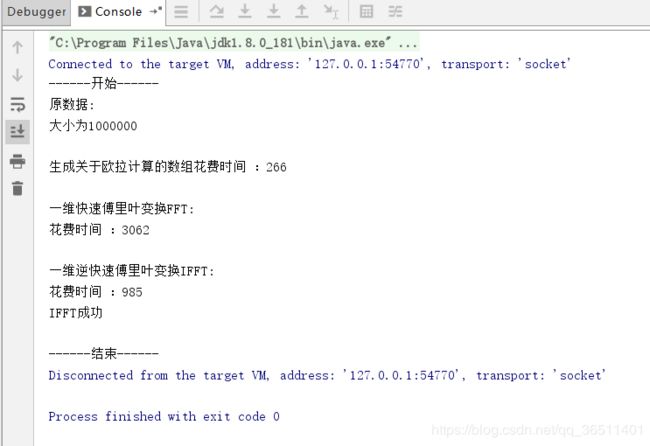
5、测试一维快速傅里叶。在文章傅里叶变换 一维快速傅里叶变换（快速的一维离散傅里叶变换、分治法）中测试大小为1百万时，花费了时间6s多。而现在只要4s左右。

6、测试二维快速傅里叶。在文章 傅里叶变换 二维快速傅里叶变换（快速的二维离散傅里叶变换、分治法）中测试大小为行为800，列为900时，花费了时间4s多。而现在只要2s左右。