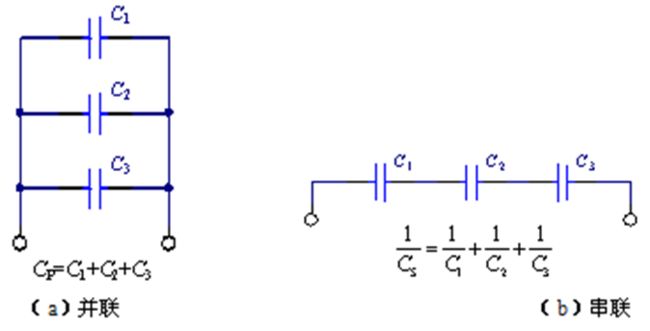
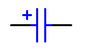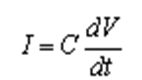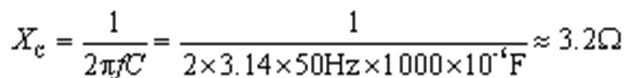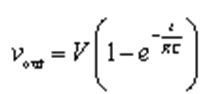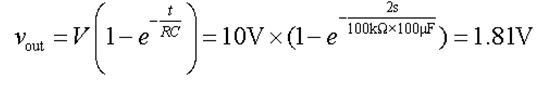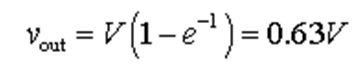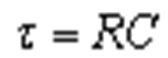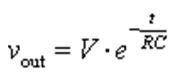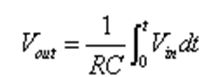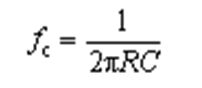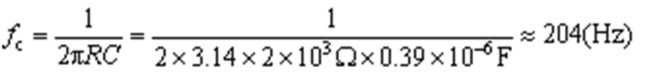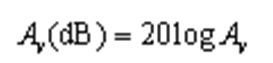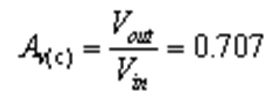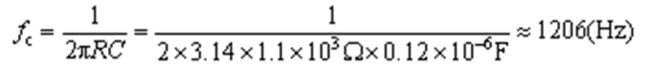电容的加入使得电路对信号有了取舍
信号的频率与幅度
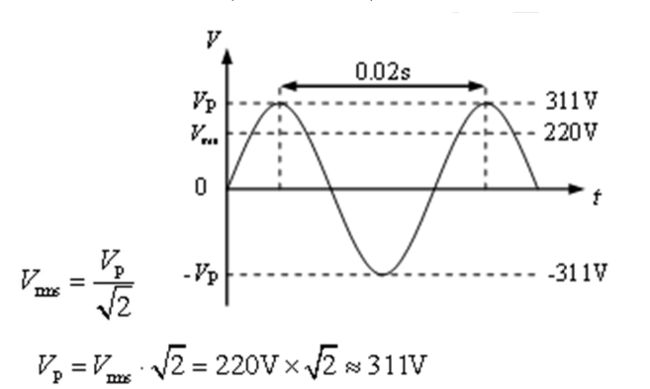
市电“电压220V”是指电压有效值,或称电压的均方根值,缩写为Vrms 。它与电压的峰值 的关系是:
幅度:是在波动或振动中距离平衡位置或静止位置的最大位移 T表示
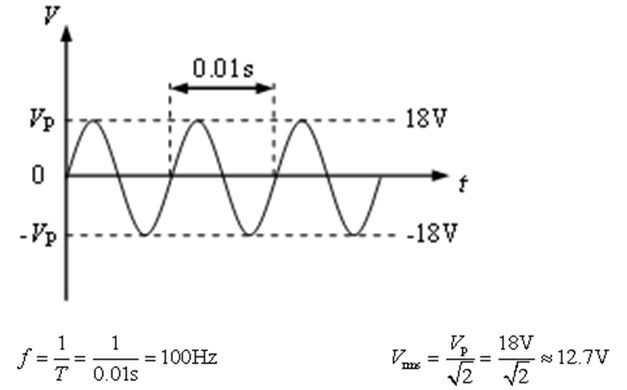
频率:单位时间内完成振动的次数;定义:物质在1秒内完成周期性变化的次数叫频率,f表示。
信号的幅度变化
两个幅度相等、频率不同的信号合成
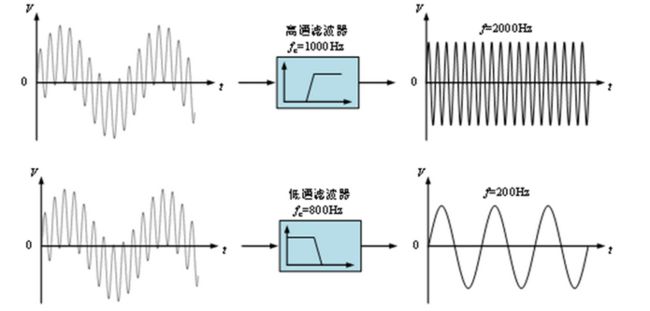
滤波器的使用
元器件A--无极性电容
电容器,简称电容,是一种由电介质分隔的两个导体构成的基础元器件。
可变电容内部有一个固定的多叶金属板,转轴带动另一个可移动多叶金属板,并控制两个多叶金属板的重叠(但不接触)面积,从而改变容量。可变电容的电介质一般为空气
隔直通交
“隔直”是隔离直流信号,“通交”是通过交流信号,这是电容一个最本质的特性。
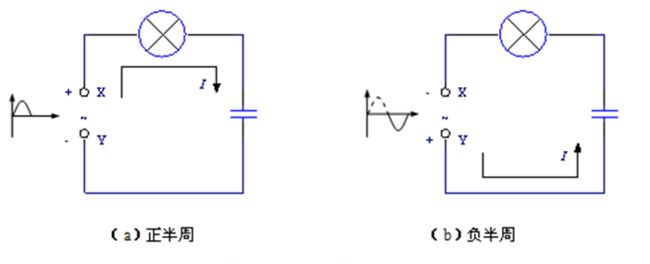
正半周时,电流顺时针流动向电容充电,电路因有电流产生而灯泡点亮。负半周时,电流逆时针流动向电容反向充电,电路有电流,灯泡还是会被点亮。
PS:电容因为内部由电介质(绝缘体)分割两个导体,所以电流实际是不能通过电容的。只不过充电过程中,电子在运动到电容极板的过程中在电路里产生了电流于是在电路中的灯泡因为有电流流过而而被点亮。
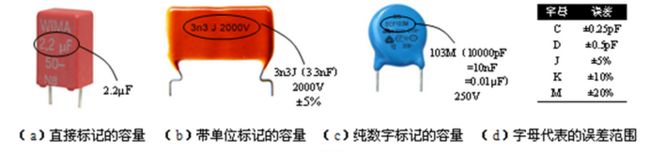
电容的容量
电容的容量描述的是电容存储电荷的能力,容量越大,表明电容能存储的电荷越多。单位法拉,用字母“F”来表示。其他单为:
1F=103mF 1mF=103µF 1µF=103nF 1nF=103pF
标记电容容量的方法: 1. 电容表面印有容量的数值和单位 2.容量加单位缩写 3.纯数字
无极性电容的种类
无极性电容的种类:瓷片电容(ceramic)、云母电容(mica)、涤纶电容(polyester)、镀金属塑料膜电容(metallised plastic film)、聚丙烯电容(polypropylene)、纸介电容(paper)等。
元器件B--极性电容
极性电容(器)与非极性电容的最大区别在于管脚有正、负极之分,在电路中不能混用。
极性电容的特性
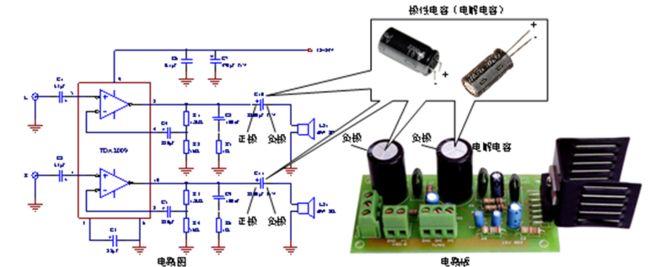
极性电容除了隔直通交特性外,更多体现的是储能特性。在 图中,充电之后的电 容存储电荷,断开开 关,电容和电阻形成 一个闭合的环路,电 容开始向电阻放电, 金属板间电压降低, 至0V时放电停止,电 路中电流消失。在放 电过程中,电容好像一个电池,向电路提供电流,这就是电容的储能特性。
极性电容的种类
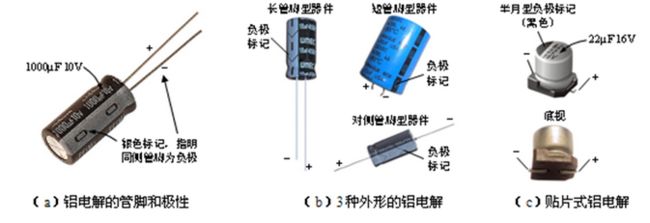
铝电解电容(aluminium electrolytic),简称铝电解,是一种最为常用的极性电容。
钽电解电容(tantalum),简称钽电解,是另一种极性电容。它与铝电解相比,具有较高的稳定性、较小的误差、较小的漏电流等特点。
电路与应用A——电容的应用基础
电荷与能量的存储
与电阻不同,流经电容的电流与电压并不是简单的线性关系,而是用以下这个公式来计算:
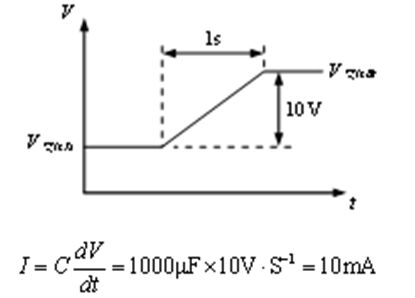
dV/dt表示的是电容两端电 压的变化率,C是电容的容 量。假如在容量为1000µF 的电容两端出现如图示的 电压变化,于是dV/dt=10。 可得电容的电流大小为:
容抗
描述的是电容对信号的阻碍作用,一般用“XC”来表示。容抗它不但取决于电容的容量,还受制于信号的频率。容抗的计算式为
其中,f为信号的频率,C为电容的容量。当f的单位为Hz,C的单位为F时,XC的单位为Ω。假如有一个50Hz的交流信号经过容量为100µF的电容,则容抗为:
如果有一个直流信号经过相同的电容,则容抗为(直流信号的频率f=0Hz):
容抗XC为无穷大,说明电容对于直流信号有无穷大的阻碍,相当于断开。这也就是“隔直通交”的定量解释。
可见,信号频率f越大或容量C越大,容抗XC越小,对信号的阻碍也就越小。
相移
描述的是信号相位的改变。当有一个正弦信号通过电阻时,电阻两端的电压和电流会同时达到峰值,称之为电压与电流同相
当正弦信号通过电容时,电容两端的电压与电路中的电流的变化并不同步。当电流达到最大值时,电压却为0V,反之亦然。电容两端的电压与电流之间有90°的相差,并且电流领先于电压的变化。
电路与应用B——RC电路与时间常数
电容充电
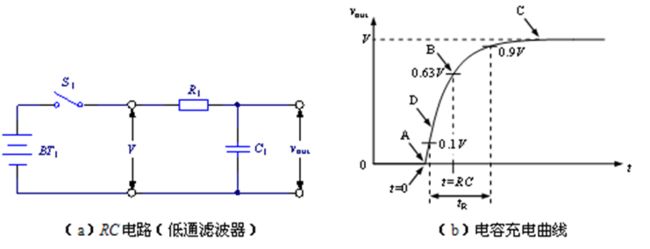
RC电路:当开关S1闭合时,电源BT1可通过电阻R1向电容C1充电。在开关S1闭合的一瞬间开始,电容C1刚刚开始充电,此时C1两端 的电压vout将要变大,如图中的 A点。
随着充电的进行,电容C1两端的电压vout不断变大,最终等于电源的电压V,图中的C点。充电过程中某一时刻电容两端的电压计算公式:
其中,V为RC电路的输入电压, e=2.71828…。t是充电开始之后的某一个时间点。R、C分别是电路中电阻R1阻值和电容C1容量的数值。
假设BT1的电压V=10V,R1=100kΩ、C1=100µF,在电容C1开始充电2秒后两端的电压为:
有一个特殊的时刻,也就是当t=RC时,RC电路的输出电压为:
也就是说,当电容充电了t秒之后,如果t等于电阻阻值和电容容量的乘积,那么RC电路的输出电压 为输入电压V的0.63倍。
在电子学中,把RC电路中 电阻阻值和电容容量的乘 积称为RC时间常数,用希 腊字母“τ”表示,于是有:
电容的放电
在放电过程中电容两端的电压可由下式计算:
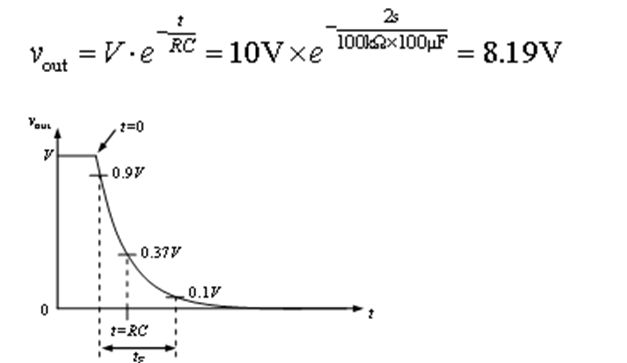
如果电源BT1电压V=10V,R1=100kΩ、C1=100µF,则在电容充满电后开始放电2秒后电容两端的电压为:
RC电路的延时应用
输入信号由低向高跳变时,经过缓冲1后输入RC电路。电容充电的特性使B点的信号并不会跟随输入信号立即跳变,而是有一个逐渐变大的过程。当变大到一定程度时,缓冲2翻转,在输出端得到了一个延迟的由低向高的跳变。
电阻耦合与电容耦合
电阻耦合
无源滤波器
滤波器(filter)是一种去掉输入信号中某一特定频率段成分的电路。
假如高通滤波器中电阻R1=2kΩ、电容C1=0.39µF,则高通滤波器的截止频率fc为:
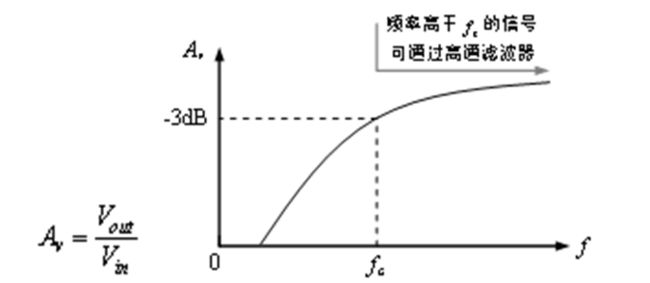
这样,只有频率高于204Hz的信号才可以通过高通滤波器,而低于204Hz的信号将被滤除掉。
无源高通滤波器的幅频特性:横坐标(f)是输入信号Vin的频率,纵坐标(Av)是输出信号Vout的幅度与输入信号Vin的幅度的比值,也就是电路的电压增益(也叫电压放大倍数):
电子学中还常常使用分贝为单位来表示电路的增益,计算方法是对电压增益取以10为底的对数并乘以20,转换式为:
对于高通滤波器来说,当输入信号Vin的频率等于截止频率fc时,输出信号Vout与输入信号Vin的幅度比值为0.707,即:
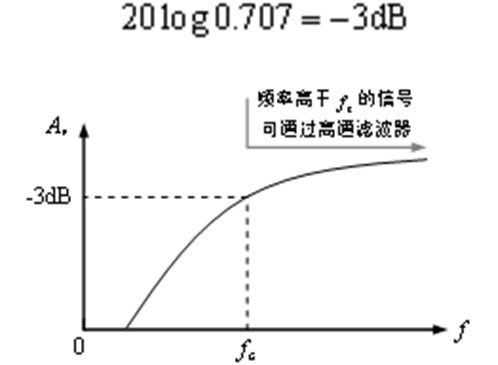
如果使用分贝为单位:
无源低通滤波器的截止频率fc:
假如电阻R1=1.1kΩ、电容C1=0.12µF,低通滤波器的截止频率为: