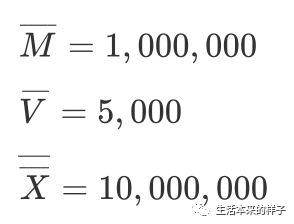罗马数字是总共由 7 个字母符号表示:I(1)、V(5)、X(10)、L(50)、C(100)、D(500)和 M(1000)。
表一:罗马数字对应的阿拉伯数字
| 罗马数字 | 阿拉伯数字 |
|---|---|
| I | 1 |
| V | 5 |
| X | 10 |
| L | 50 |
| C | 100 |
| D | 500 |
| M | 1000 |
他们按照以下 4 个规则可以组合成表示任意的正整数。
(1)
一个罗马数字重复多少次,就表示这个数多少倍,比如罗马数字 I 表示的是数字 1,重复两次,即 II,表示的数字是 2,同理,III 表示数字 3,XX 表示数字 20,CC 表示数字 200 等;
需要注意的是,同一个罗马数字最多只能连续重复 3 次,如数字 400 就不能表示为 CCCC(重复了 4 次),而是要用 CD 来表示,数字40不能表示为 XXXX(同样重复了 4 次),而要表示为 XL 等。
但有一种特殊情况,因为古罗马人用 IV 作为古罗马神话主神朱庇特(IVPITER,古罗马字母里没有 J 和 U)名字的简写,他们不希望神的名字看上去像个数字,因此有时用 IIII 代替 IV。
另外,符号 D、L 和 V 不可以连续重复出现,比如用 DD 表示 1000 的写法是错误的,正确的是要用 M,表示 1500 的罗马数字是 MD,而不是 DDD。
(2)
如果在较大的罗马数字后面(或右边)放置较小的罗马数字,表示的数字为这些数字相加得到的数,如较大的罗马数字 V 后面放置较小的罗马数字 I,即 VI,表示的数字则为 V 与 I 相加得到数 6。
同理,
VII = 7 (5 + 2 = 7)
LXXX = 80 (50 + 10 + 10 + 10 = 80)
MC = 1100 (1000 + 100 = 1100)
(3)
如果在较大的罗马数字前面(或左边)放置在较小的罗马数字,表示的数是用较大的数减去较小的数所得到的值,如较大的罗马数字 V 前面或左边放置较小的罗马数字 I,即 IV,表示的数字则为 V 减去 I 得到的数 4。
同理,
IX = 9 (10 – 1 = 9)
XC = 90 (100 – 10 = 90)
用这种方式来表示罗马数字时,有以下几点需要注意:
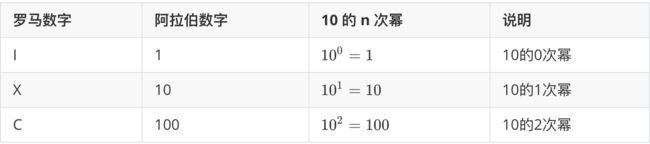
i) 充当减数的只能是 I,C 或 X,不能是 L 或 V,即罗马数字对应的数是 10 的 n 次幂才能充当减数。另外,由于 M 在罗马字母中表示的数最大,也不能充当减数(罗马数字没有 0 或负整数)。
被减数 - 减数 = 差,
如 32 - 10 = 22,
被减数是 32,减数是 10,差是 22。
表二:减数的只能是 I,C 或 X
比如数字 45,
不能写成 VL(50 - 5),
而是要写成 XLV(XL + V,即 40 + 5);
ii) 只能从一个罗马数字中减去另一个罗马数字,而不能减去两个或两个以上的罗马数字,比如说数字 8,
不能写成 IIX(X - I - I,即 10 - 1 - 1 = 8),
而是要写成 VIII(V + I + I + I,即 5 + 1 + 1 + 1 = 8);
iii) 从一个罗马数字(设为 a)中减去另一个罗马数字(设为 b)所得的差(设为 c),不能超过减数(即 b)的 10 倍以上。
例如,
你可以从数字 10 中减去 1,
因为 10 - 1 = 9,9 比 1 的 10 倍(10)小;
但是不能从数字 100 中减去 1,
因为 100 - 1 = 99,99 比 1 的 10 倍(10)大。
所以,
数字 9 可以用 IX 来表示,
但数字 100 不能用 IC 来表示,
而是要用 XCIX(XC + IX,即 90 + 9 = 99)来表示。
根据第 i) 点和第 iii) 点,可以得到以下规则:
*符号 I 只能出现在符号 V 或 X 的前面(或左边); *
*符号 X 只能出现在符号 L 或 C 的前面(或左边); *
符号 C 只能出现在符号 D 或 M 的前面(或左边)。
(4)
如果在罗马数字上方加一条横线,表示将该数值乘以 1000,即原数的 1000 倍,
如果上方有两条横线,表示的数字是原数的 1, 000, 000 倍。
如:
罗马数字举例:
尝试应用上述规则,写出以下阿拉伯数字对应的罗马数字
35,
65,
99
求解过程如下:
35 = 10 + 10 + 10 + 5,即 X + X + X + V(XXXV),所以 35 = XXXV;
65 = 50 + 10 + 5,即 L + X + V(LXV),所以 65 = LXV;
99 = (100 - 10)+(10 - 1),即 XC + IX(XCIX)所以 99 = XCIX 。