一、分析需求
1.对共享单车满意度评分数据进行清洗,去除空缺值等
2.对用户满意度分数的整体情况进行分析
3.对于收押金这一举措,用AB测试思路来检测收押金是否会影响用户满意度
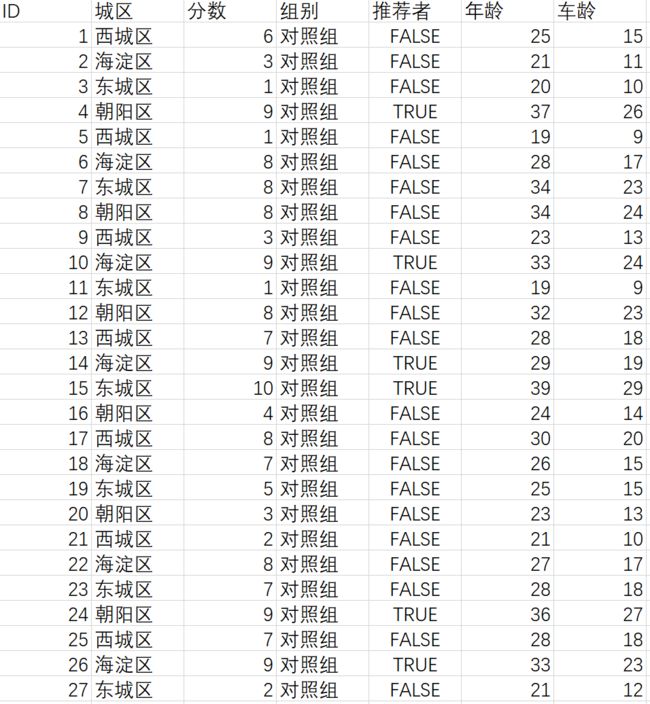
二、数据情况(实验数据)
北京四个城区调研客户对共享单车的满意程度,并分为了对照组和实验组,分别对收押金前后的满意程度进行了统计
三、分析过程
1.清洗数据填补空值
对数据进行整理清理,其中分数有些许空缺值,填补缺失值采用的统计量是去除空值后的分数的平均值,填补缺失值大小是5.458333,实现语句:
setwd("C:/Users/emera/Desktop/共享单车评分数据")
R_homework <-
read.csv("共享单车评分数据.csv",fileEncoding ="UTF-8-BOM")
#查看数据整体情况
str(R_homework)
#查看是否有空值
is.na(R_homework$城区)
is.na(R_homework$分数)
is.na(R_homework$组别)
is.na(R_homework$推荐者)
is.na(R_homework$年龄)
#填充空值
alternative_value<-
mean(R_homework$分数,na.rm = TRUE)
R_homework[is.na(R_homework$分数), "分数"] <-alternative_value
is.na(R_homework$分数)
2.对分数整体显现情况进行初步分析
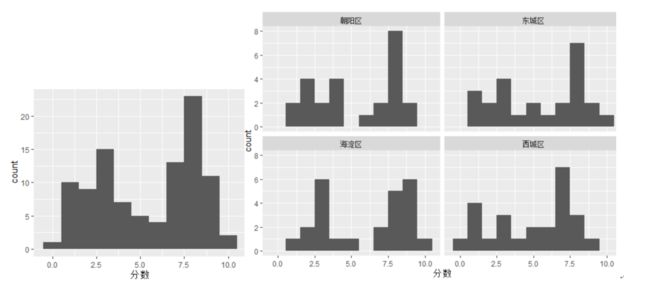
从直方图中可以看出,朝阳区和东城区给出8分的用户最多,西城区给出7分的用户最多。海淀区分数两级分化情况比较严重,给最多的分数是9分和3分,同时高分(分数7分以上)数量比其他区域高,但低分(3分以下)的数量也很高。
从箱型图中我们可以进一步看出,朝阳区、东城区、西城区用户的平均分相近,海淀区平均分最高,但是海淀区的分数也是最分散的。从小提琴图中,我们可以看到西城区高分面积最大,低分面积最小,海淀区呈现两极分化的葫芦形,东城区各分数段数量分布比较均匀,朝阳区数据离散度较小。
实现语句:
#直方图
library(ggplot2)
a <-
ggplot(R_homework,aes(分数))
a +geom_histogram(binwidth = 1)
facet_wrap(~城区,nrow=2,ncol=2)+
#箱型图
b <-
ggplot(R_homework,aes(城区,分数))
b + geom_boxplot()
#小提琴图
c <-
ggplot(R_homework,aes(城区,分数))
c +geom_violin(draw_quantiles = c(0.25,0.5,0.75))
3.各个城区用户给分和年龄关系分析
我们对散点图进行线性拟合。从图中可以看出,各个区域的样本取样较为随机,不存在某一年龄段取样集中的不合理现象。对图形进行观察,发现拟合程度都近似,各个区域打分均表现出和年龄的正相关性。其中朝阳区和东城区的拟合情况最为集中,海淀区和西城区的拟合函数更为陡峭(斜率更高)。有趣的是,各个区域25-30岁的用户打分都在拟合函数之上,25岁以下和30岁以上大多在拟合函数之下。也就是说如果我们用拟合函数最各年龄段的满意度预估,25-30岁区间的满意度更有可能高于预估值,25岁以下和30岁以上区间的满意度更有可能低于预估值。
实现语句:
#散点图拟合年龄和分数关系
g <-
ggplot(R_homework,aes(年龄,分数))
g + geom_point(alpha =0.25)+
geom_smooth(method='lm',col='red')+
theme_bw(base_family= "Avenir",base_size = 15)+
facet_wrap(~城区,nrow=2,ncol=2)+
labs(x='年龄(age)')+
labs(y='分数(score)')+
labs(title='用户满意度调查(分数与年龄关系)')
4.对“收押金”措施是否对西城区用户满意分有显著影响设计A/B测试
1.原假设H0,发红包对提升用户满意分没有影响,即未发红包对照组满意分均值X1=发红包实验组满意分均值X2
备选假设H1,发红包可对用户满意分有显著影响,即未发红包对照组满意分均值X1=!发红包实验组满意分均值X2
因为假设是问是否有显著影响,好的影响和不好的影响都包含在此假设内,因此采用双侧检测。
2.使用函数t.test()计算P值。
实现方式:
Ttestdata <-read.csv("Ttestdata.csv")
scoreA <-
Ttestdata[Ttestdata$"组别"=="对照组"&Ttestdata$"城区"=="西城区", "分数"]
scoreB <-
Ttestdata[Ttestdata$"组别"=="实验组"&Ttestdata$"城区"=="西城区", "分数"]
#进行T检测
t.test(scoreA,scoreB,alternative= ("two.sided"),conf.level = 0.95)
计算结果:
data: scoreA and scoreB
t = 0.2778, df = 20.926,p-value = 0.7839
alternative hypothesis:true difference in means is not equal to 0
95 percent confidenceinterval:
-2.079380 2.720406
sample estimates:
mean of x mean of y
5.153846 4.833333
3.按照显著性水平α=0.05看,P值0.78大于0.05,所以原假设H0成立,不能证明收押金对用户满意分有显著影响