首先要讲一下CRC16是什么 。
CRC是一种常见的校验,而CRC16呢,主要是因为校验结果是16个位,当然还有CRC8,CRC32.
你以为我就这么简单地解释吗?是的,我就这么简单的解释一下好了。当你阅读这篇文章,要想更好地理解这篇文章,你需要你去看一下什么 是CRC16校验。
我们常见的Modbus 的CRC校验,也是CRC16校验的一种。接触过modbus 协议的人,应该对CRC16校验就不陌生了。
通俗的讲,CRC16是一条运算公式,而它的运算数据至少是一个字节。它的运算过程就是将一个字节的每一个位,都参与计算 。
下面是我从百度百科找来的一段描述:
硬件计算过程
1.设置CRC寄存器,并给其赋值FFFF(hex)。
2.将数据的第一个8-bit字符与16位CRC寄存器的低8位进行异或,并把结果存入CRC寄存器。
3.CRC寄存器向右移一位,MSB补零,移出并检查LSB。
4.如果LSB为0,重复第三步;若LSB为1,CRC寄存器与多项式码相异或。
注意:该步检查LSB应该是右移前的LSB,即第3步前的LSB。
5.重复第3与第4步直到8次移位全部完成。此时一个8-bit数据处理完毕。
6.重复第2至第5步直到所有数据全部处理完成。
7.最终CRC寄存器的内容即为CRC值。
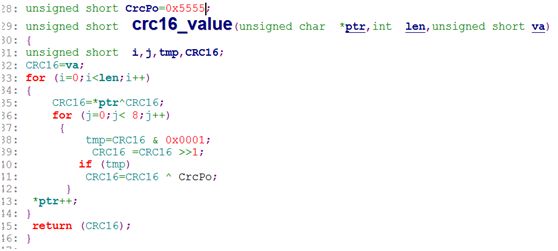
下面我们再来看一下一段CRC16 的算法:(也是网上找的)
其中prt是要计算的数据,len是字节个数,va是多项式。
那么重点来了。
从硬件计算过程和算法函数可以看到, 这个CRC16算法中,最重要的一个参数就是多项式了,当然还有一个辅助参数是初始值。
不同的CRC16,其多项式是不一样的。
而不同的初始值与多项式,就组成了不同的CRC16校验。
可以看出,常见的CRC16无非也就这几种,其实还有一个常见的多项式是A001。
不管CRC16 怎么变化,也是万变不离其宗的。
下面我们就展开这个不离其宗进行介绍,如何有效的去破解CRC16.
情况一 修改最后一个字节为00或80.
破解方法:
将xx xx xx 00 的CRC16 值 0xYYYY
与xx xx xx 80 的CRC16 值 0xZZZZ 进行异或,
即0xYYYY异或0xZZZZ 即可得到多项式 0xNNNN
举例
以一个标准的CRC16为例,其多项式为0xA001
分别计算11 22 33 44 00 和11 22 33 44 80的结果
得到的结果为
11 22 33 44 00 7435
11 22 33 44 80 D434
7435与D434 异或得到的结果为A001 .
我们再拿一个非标准的多项式,比如0x1234为例。
分别计算11 22 33 44 00 和11 22 33 44 80 的结果
11 22 33 44 00 17FF
11 22 33 44 80 05CB
然后将0x17FF和0x05CB进行异或,得到的结果就是0x1234。
所以,得到的一个结论就是:
在一串数组或报文里,如果只改变最后一个字节的最后一个位,得到的两个CRC16结果进行异或,算出来的就是多项式。
为什么会得出这样的结论呢
让我们可以看一下代码运算的最后一步。
1122334400和1122334480的差别就是最后一个位,因为最后一个字节的最高位是最后参与运算的。而运算就是将从1122334400运算出来的结果,再判断最后一位是否为1,如果为1,再将结果运行,也就是和多项式进行异或,也就是1122334480在整个运算过程,在运算到最后一个位的时候,结果是0x17FF了,这时候,再判断最高位是否为1,然后最高位是1,再将0x17FF与多项式0x1234进行异或,得到的0x05CB。就是1122334480的CRC结果了。
所以,我们要反计算出多项式值,就需要找出至少两组报文,只修改最后一个字节的最高位,将得出的两个CRC结果进行异或,就反算出了多项式了。
而初始值一般是0x0000或者0xFFFF。如果将0x0000,0xFFFF代入计算都得不出结果,一般的话,可以将初始值从0x0000到0xFFFF遍历,就可以计算出来的。即便遍历一个U16花的时间也就几秒钟了。这就是所谓的辅助暴力破解。
下面我们就以一组数据为例,我先不要说多项式是多少。根据下面的数据计算出多项式。
1122334400 66BB
1122334480 259A
然后我们把66BB和259A进行异或,得到的结果是 4321 。
没错,多项式就是4321,不知道你有没有算对呢。咋一看,反计算CRC16也不是很难呀。
看一下工具计算的结果,我没有蒙你们。
情况二:无法改变最后一个字节的最高位。
比如,只能改变倒数第二个字节,怎么办呢。或者其它字节的
这种情况下就不能直接将CRC结果异或了。
举例来说吧。还是标准的CRC16, 多项式是A001。
112233440055 2874
112233448055 E815
112233440066 3D34
112233448066 FD55
2874异或E815 ,结果为 C061
3D34异或FD55 ,结果为 C061.
可以看出,在数组里,如果只改变其中一个位,其它元素不变的情况或者变成一样的话,有一个位的0或者1 变化得到的两个CRC16值进行异或,异或的结果是一样的。
只是,如果变化的是最后一个字节的最高位,那两个CRC16值异或的结果直接就是多项式了。
像这种情况怎么办呢,明明多项式是A001。但是CRC16值异或的结果确是C061。
我们知道数组112233440055 里,肯定存在一个或多个多项式和初始值,经过CRC16运算,得到的结果是2874。
我们写个程序遍历一下。
unsigned short crc16_crc(unsigned char *ptr,int len,unsigned short va) //
{
unsigned short i,j,tmp,CRC16;
CRC16=0x00;
for (i=0;i { CRC16=*ptr^CRC16; for (j=0;j< 8;j++) { tmp=CRC16 & 0x0001; CRC16 =CRC16 >>1; if (tmp) CRC16=CRC16 ^ va; } *ptr++; } return (CRC16); } 这个函数呢,prt是要计算的数据,len是字节个数,va就是多项式。 也就是我们要通过这个函数来遍历所有的多项式,看看有多少个结果是匹配的。 (这里为什么会有0x2874和0x7428呢,因为有些是低字节在前,有些是高字节在前) 可以看出,刚好值是A001。为什么呢。因为我刚好设置的初始值是0x000,刚好遍历出来的结果,得到的就是有A001。这个不算啊。我们换个初始值再重新计算一遍。假如初始值你不知道,但是多项式就是0xA001。我们再来一遍。 于是得到的新的结果是: 112233440055 5FC8 112233448055 9FA9 112233440066 4A88 112233448066 8AE9 我们还是先使用老办法 5FC0异或9FA9,结果是C061 4A88异或8AE9,结果是C061. 惊喜不惊喜,意外不意外。这个初始值呢,后面再给大家讲一讲,为什么一开始可以不关心初始值。 然后我们程序再跑一遍,注意,这时候跑出来的结果是错误的 因为我的crc16函数默认初始值是0x0000,但实际使用的初始值不是0000,遍历每一个多项式。执行下来,可以说1S就可以得到遍历结果了,结果是B562。这个多项式和A001差太远了吧。当然,你也可以说将初始值和多项式一起遍历,肯定可以得到出结果的。要遍历40亿遍呢。这个时间估计你不会乐意等的。而且,多项式和初始值一起遍历,可能得到有很多的组合。如果得出100个组合,那你是否又怎么从这100个组合里选出哪个多项式和初始值呢。当然可以再将这100个组合再重新遍历呢。 确认地说,按理我对CRC16地理解,这个CRC16校验是一一对应型。 也就是给定两个字节,也就是一个U16从0000到FFFF作CRC16运算,会得到65536个结果。也是每一个U16的数据,都对应一个U16的结果,没有重复的。 简单地说,假如我有1,2,3,4这四个数作密文,密文对应关系为: 1>2 2>4 3>1 4>3 是这样一种对应关系。只是CRC16呢,是从0到65535都可以找到另一个0到65535里的一一对应关系。 如果你理解这个,你会发现,当将多项式和初始值一起遍历,你会发现,每一个初始值,都能找到一个多项式经过CRC16运算,会匹配到结果的。这个就是所谓的碰撞。那遍历下来了,你将得到可能65536个结果,或者更多。那你还需要将这65536个结果里再代入到另一个报文里去验证是否正确。这个时间和工作量是比较大的,如果你没有一台32核CPU的电脑或者一颗愿意等待的心,我劝你还是放弃这个方法。 下面就是我的方法了 情况二的破解方法: 112233440055 5FC8 112233448055 9FA9 112233440066 4A88 112233448066 8AE9 5FC0异或9FA9,结果是C061 4A88异或8AE9,结果是C061. 我们假设这四组数据,不知道多项式和初始值。虽然我告诉你,我是用A001作测试的,你都不敢相信。 下面的方法很重要了。 废话多说,直接上代码: unsigned short crc16_crc(unsigned char *ptr,int len,unsigned short va) // { unsigned short i,j,tmp,CRC16; CRC16=0x00; for (i=0;i { CRC16=*ptr^CRC16; for (j=0;j< 8;j++) { tmp=CRC16 & 0x0001; CRC16 =CRC16 >>1; if (tmp) CRC16=CRC16 ^ va; } *ptr++; } return (CRC16); } int main() { int i; unsigned short out; unsigned short out2; unsigned char test_buff1[]={0x11,0x22,0x33,0x44,0x00,0x55}; unsigned char test_buff2[]={0x11,0x22,0x33,0x44,0x80,0x55}; unsigned char test_buff3[]={0x11,0x22,0x33,0x44,0x00,0x66}; unsigned char test_buff4[]={0x11,0x22,0x33,0x44,0x80,0x66}; for(i=0;i<0xffff;i++) { out=crc16_crc(test_buff1,sizeof(test_buff1),(unsigned short)i); out2=crc16_crc(test_buff2,sizeof(test_buff2),(unsigned short)i); if(((out^out2)==0xC061)) { printf("第一组和第二组数据结果 :%x \r\n",i); } } for(i=0;i<0xffff;i++) { out=crc16_crc(test_buff3,sizeof(test_buff3),(unsigned short)i); out2=crc16_crc(test_buff4,sizeof(test_buff4),(unsigned short)i); if(((out^out2)==0xC061)) { printf("第三组和第四组数据结果 :%x \r\n",i); } } 到了这里,估计你还在想这个结果怎么来着,为什么这样计算就可以得到结果呢。 当然,有可能得到的结果是有多个,但是一般结果不会超时10个。而且,基本上用两组数据运算,得到共同结果的,肯定就是多项式值了。 到这里,你可能会问,我知道了多项式,不知道初始值怎么办,那简单,可以将初始值遍历一下就出来了。 函数里prt是要校验的数据,len是字节个数,va是初始值。多项式就是CrcPo=0xA001. 然后遍历得到结果,初始值是0X1234。 下面我们再破解一个新的CRC16. 还是原来的数据,但是多项式和初始化我先不告诉你。你跟着方法来走一遍。 112233440055 1E67 112233448055 6FCD 112233440066 3132 112233448066 4098 (十六进制) 1E67异或6FCD是71AA 3132异或 4098 也是71AA 现在我们不知道多项式和初始值,我们先用刚才的方法找出多项式。 这样,我们就找出了多项式值是0x5555。下面我们再找出初始值。 可以看出,有两个结果匹配出来了。但为什么会有两个初始值可以匹配出来呢。 是因为我使用的多项式值是0x5555,因为不是所有的多项式都能保证CRC16是一一对应的。 那么问题就在这里。初始值可以设置不同的值,多项式值是不是可以任意取呢。 不是的。 因为这个CRC16的算法中,是一个特殊的公式计算。并不是所有的多项式都能满足CRC16的一一对应关系。有可能某些多项式,会出现1对应999,10也对应999,100也对应999。 这种情况下,碰撞的概率就会更大了。碰撞是用于破解协议和密码中常使用的手段。往往是根据协议或加密算法中,找到一定的漏洞之后,再加以一定的碰撞测试,就有可能找到匹配出密码所需要的数据,从而完成非正常解密,也达到破解的过程。 在常见的CRC16算法中,常见的还有查表法,为什么可以使用查表法呢,就是输入和输出是一一对应的。输出结果是U16,就能保证输入的U16里,没有一个输出结果是重复的。根据这个特性呢,可以将CRC16算法隐藏重要数据。文章最后讲到。 所以,情况二的破解方法就是, 1 先找到二组或四组数据。(只改变其中一个位的,其它字节数据不变) 112233440055 1E67 112233448055 6FCD 112233440066 3132 112233448066 4098 (十六进制) 2 将对应的两组数据的CRC16进行异或。 1E67异或6FCD是71AA 3132异或 4098 也是71AA 3 通过遍历多项式来匹配异或结果与我们手动异或结果是一致的。 4 找出多项式后,再将多项式代入,遍历初始值。 下面对CRC16 作个大概的总结吧 以上方法呢,是针对普通的CRC16校验的。 如果你细心观察网上的代码或者别的介绍,你会发现还有什么右移和左移的区别。 我举例使用的代码是右移的,你可以看到函数里,是使用了右移的操作。因为这个算法是使用了右移的,所以在计算最后一个字节的话,最高位是参与最后一次运算的,这使得情况一中,如果只改变化最后一个字节的最高位,得到的两个CRC16值进行异或,得到的就是多项式了。 如果你的算法使用的是左移,那么参与最后一次运算的就是最后一个字节的最低位了。这时候应该改变的是最后一个字节的最低位了。 延伸扩展一下。 CRC16除了作校验之外,还有什么功能呢。 有的。 可以用于隐藏特殊字节或重要字节进行传输。 这个功能估计99%接触CRC16的人都不太使用过或了解过吧。 举例说明一下吧,以标准的CRC16为例。因为标准的CRC16是输入输出是一一对应的。 比如我有一段报文要传输,112233440088 ,其中,88 这个字节是很重要的,是我不想通过明文传输让别人发现的。 112233440088的CRC校验是71B4. 这样我就可以将88隐藏起来。 得到新的报文是 112233440071B4. 在接收设备接到这个报文之后,由于协议是双方知道的,接收设备就可以从112233440000到1122334400FF进行遍历,找到一个唯一的值计算出来的CRC16是71B4。那么就知道这个重要的数据就是88了。 然后发送方可以将112233440071B4再计算CRC16再发送, 112233440071B45033 就可以保证数据的完整性,也增加了破解的难度以及大大降低了碰撞的概率,也更容易混淆破解的人了。 一个CRC16 可以隐藏两个字节。 一个CRC8可以隐藏一个字节。 一个CRC32可以隐藏四个字节。 这种算法中,往往是用于保护重要的数据,同时也增加破解的难度。当然,使用这种算法的,一般主要是国外的设备为主,别问我是怎么知道的。 最后特别感谢 http://www.21ic.com/tools/HotPower/HotCRC.html 这个在线计算CRC工具,给我的测试提供了便利。也推荐给大家。 后期还会写一些关于编程,协议,工控等偏向技术的文章,敬请关注与留言。 如有转载,请注明出处 https://www.jianshu.com/p/1c1f986b0ac8