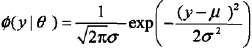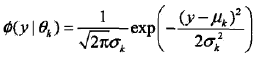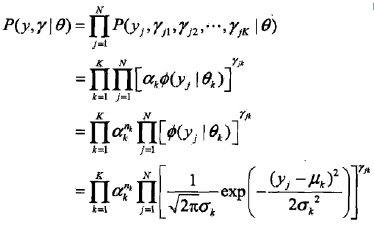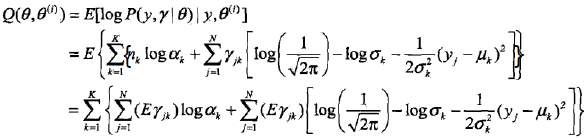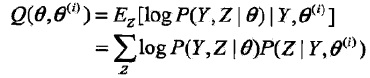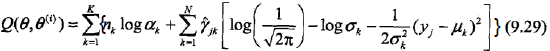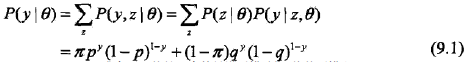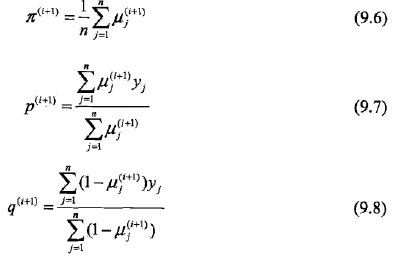在开始讲解之前,我要先给看这篇文章的你道个歉,因为《2012.李航.统计学习方法.pdf》中该节的推导部分还有些内容没有理解透彻,不过我会把我理解的全部写出来,而没理解的也会尽可能的把现有的想法汇总,欢迎你和我一起思考,如果你知道为什么的话,还请在评论区留言,对此,不胜感激。
当然,若你对EM算法都一知半解,那还是去看一下我总结的“EM算法 - 1 - 介绍”吧,不然你连我问的疑问都看不懂。
OK,mission start!
单高斯分布模型(GSM)
首先,为了更好的说明高斯混合模型,这里先简单介绍下GSM,GSM看名字就知道,模型中只有一个高斯分布,只不过在处理问题时我们会遇到:只知道结果,但不知道能实现该结果的最佳高斯分布,即:不知道高斯分布的参数。
这个问题解决起来很容易,只要用极大似然估计就可以了。
从几何上讲,单高斯分布模型在二维空间应该近似于椭圆,在三维空间上近似于椭球。遗憾的是在很多分类问题中,属于同一类别的样本点并不满足“椭圆”分布的特性。这就引入了高斯混合模型。
高斯混合模型GMM
什么是GMM
GMM简单的说就是从几个GSM中生成出来的。即,如果GSM的概率密度函数用
表示的话,那GMM就是:
称为第k个分模型,其中θk= (μk,σk2)。
tip: 9.24式中的ak是某个高斯分布的权值,这就是说:样本集合Y中的各个元素一定是从这K个高斯分布中得到的,如果把所有高斯分布的重要性定义为1的话,那其中第k个高斯分布的重要性就是ak,其中a1+a2+...+aK = 1。 用另一种方式理解就是:所有的高斯分布在样本集合中被使用的概率一共是1, 于是第k个高斯分布被使用的概率就是ak,其中a1+a2+...+aK = 1。 |
为什么这么重视GMM,而不使用其他的分布?
实际上不管是什么分布,只K取得足够大,这个分布模型就会变得足够复杂,就可以用来逼近任意连续的概率密度分布。只是因为高斯函数具有良好的计算性能,所GMM被广泛地应用。
GMM的EM算法的推导
假设观测数据y1, y2,..., yN由GMM生成
其中,θ = (a1,a2, ..., ak; θ1, θ2, ..., θk)。
我们的目标是用EM算法估计GMM的参数θ。
1,明确隐变量,写出完全数据的对数似然函数
可以设想观测数据yj,j = 1, 2,..., N,是这样产生的:首先依概率ak选择第k个高斯分布分模型φ(y |θk);然后依第k个分模型的概率分布φ(y |θk)生成观测数据yj。
这时观测数据yj是已知的,观测数据yj来自的第k个分模型是未知的(k =1, 2, .., K),于是这个就是隐变量,我们用rjk表示,其定义如下:
PS:隐变量rjk是0-1随机变量。
有了观测数据yj及未观测数据rjk,那么完全数据是
(yj,rj1, rj2, ..., rjk), j = 1, 2, ..., N
于是,可以写出完全数据的似然函数
式中
tip: 第一个等号:在满足θ的高斯分布中,第j样本点出现的概率是P(yj, rj1, rj2, ..., rjK | θ),于是代表“所有的样本点出现的概率”的P(y,r | θ)就推出了第一个等号。 第二个等号:由9.27式可得,若第j个观测来自第k个分模型时,rjk=1,即,akφ(yj|θk)]^rjk = akφ(yj|θk)],反之,akφ(yj|θk)]^rjk = 0。 于是将K个akφ(yj|θk)]^rjk连乘,就表示了第j个样本集合属于第k个分模型,即P(yj, rj1, rj2, ..., rjK | θ)的展开 后面两个等号是基本的数学知识,就不再解释了。 |
那么,完全数据的对数似然函数就是
2,EM算法的E步:确定Q函数
tip: 上面的第三个等号的推导,就是把(a式)中的nk带进去,然后把E放到里面。 |
疑问1: 在上一个总结中已经知道Q函数的定义是 于是,上面的Q函数是怎么对应到Q函数的定义的? 或者说怎么用Q函数的定义来推导出上面的式子,即: Q(θ, θ(i)) = E[logP(y, r|θ)|y, θ(i)] = logP(y, r |θ)P(r | y, θ(i)) = ??? |
![]() 是在当前模型参数下第j个观测数据来自第k个分模型的概率,称为分模型k对观测数据yi的响应度。
是在当前模型参数下第j个观测数据来自第k个分模型的概率,称为分模型k对观测数据yi的响应度。
疑问2: 上面推导的第二个等号和第三个等号怎么得来的? |
最后将
代入9.28式,即得
3,确定EM算法的M步
这一步就简单了,Q函数已经知道,即9.29式,那对Q函数中的θ对应的各参数求偏导,并令其为0就可以了,其结果如下:
4,重复以上计算,知道对数似然函数不再有明显的变化为止。
GMM的EM算法的整理
输入:
观测数据y1, y2,..., yn,高斯混合模型;
输出:
高斯混合模型参数;
解:
例子(三硬币模型)
假设有3枚硬币,分别记作A, B,C。这些硬币正面出现的概率分别是π,p和q。
进行如下硬币实验:
先投掷硬币A,根据其结果选B或C,正面选硬币B,反面选C。
然后投掷选出的硬币,若投掷的结果是正面则记做1,反之记做0。
独立的重复n此实验(这里,n=10),观测结果如下:
1,1,0,1,0,0,1,0,1,1
假设只能观测到投掷硬币的结果,不能观测投掷硬币的过程。问:如何估计三硬币正面出现的概率,即,三硬币模型的参数。
解:
1,我们先整理下思路。
三硬币模型可以写作
其中,θ = (π, p, q);y是观察到的硬币最终的正反面;Z是硬币A的投掷结果,是没有未观察到的,是隐变量。
然后将观测数据表示为Y =(Y1, Y2, ..., Yn)T,未观测数据表示为Z = (Z1, Z2, ..., Zn)T,则观测数据的似然函数为
即
然后要求是求模型参数θ的极大似然估计。
那么我们就利用上面的算法。
先选取参数的初值,记做θ(0)= (π(0), p(0), q(0)),然后不停的迭代下面的E步和M步计算参数的估计值,直至收敛。
假设第i次迭代后参数的估计值为θ(i)= (π(i), p(i), q(i)),则EM算法的第i+1次迭代如下。
E步:计算在模型参数θ(i)下观测数据yj来自投掷硬币B的概率
M步:计算模型参数的新估计值
2,开始进行数字计算
假设模型参数的初值为
π(0) = 0.5, p(0) = 0.5, q(0) = 0.5
第一次迭代,由9.5式,对yj = 1与yj = 0均有μj(1) = 0.5
利用迭代公式9.6 ~ 9.8,得到
π(1) = 0.5, p(1) = 0.6, q(1) = 0.6
第二次迭代,由9.5式得μj(2) = 0.5
利用迭代公式9.6 ~9.8,得到
π(2) = 0.5, p(2) = 0.6, q(2) = 0.6
第二次迭代时参数就不再变化了,因此迭代停止,于是模型参数θ的极大似然估计就的出来了,即
π = 0.5, p =0.6, q = 0.6
tip: 如果取初值π(0) = 0.4, p(0) = 0.6, q(0) = 0.7,那么得到的模型参数的极大似然估计是π = 0.4064, p = 0.5368, q = 0.6432。 这就是说,EM算法与初值的选择有关,选择不同的初始值可能得到不同的参数估计值。 |
参考资料:
http://www.cnblogs.com/zhangchaoyang/articles/2624882.html
转载自:http://blog.csdn.net/xueyingxue001/article/details/51374199