HD 钱包是目前常用的确定性钱包 ,HD 是 Hierarchical Deterministic(分层确定性)的缩写。所谓分层,就是一个大公司可以为每个子部门分别生成不同的私钥,子部门还可以再管理子子部门的私钥,每个部门可以看到所有子部门里的币,也可以花这里面的币。也可以只给会计人员某个层级的公钥,让他可以看见这个部门及子部门的收支记录,但不能花里面的钱,使得财务管理更方便了。
BIP 32是 HD 钱包的核心提案,通过种子来生成主私钥,然后派生海量的子私钥和地址,但是种子是一串很长的随机数,不利于记录,所以我们用算法将种子转化为一串助记词 (Mnemonic),方便保存记录,这就是 BIP 39,它扩展了 HD 钱包种子的生成算法。BIP43 对 BIP32 树结构增加了子索引标识 purpose 的扩展 m/purpose'/ *。 BIP44是在 BIP43 和 BIP32 的基础上增加多币种,通过 HD 钱包派生多个地址,可以同时管理主网和测试网的比特币,BIP44 提出了 5 层的路径建议,如下:
m/purpse’/coin_type’/account’/change/address_index,
BIP44 的规则使得 HD 钱包非常强大,用户只需要保存一个种子,就能控制所有币种,所有账户的钱包。
BIP39助记词
一组容易记忆的词 - 用于生成确定性钱包。BIP39 包含俩部分内容 第一部分 是生成助记词 第二部分讲助记词转化成种子 种子(Seed)之后会在BIP32 用生成确定性钱包。
助记词的作用
相对于二进制或者十六进制,单词和句子更容易让人们记住。生成助记词 熵的位数必须是32bit的倍数编码,随着熵的提高 安全性提高 助记词也变多了我们将初始熵长度称为ENT。ENT允许的大小是128-256位。校验和(CS)的长度为熵的长度/32 位
该校验和被附加到初始熵的末尾。接下来,这些连接的比特被分成11位的组,每个编码从0到2047的数字,用作词表中的索引。最后,我们将这些数字转换成单词,并将这些连词作为助记句。
下表以文字描述了初始熵长度(ENT),校验和长度(CS)和生成的助记符句子(MS)的长度之间的关系。
总结一下
1.创造一个128到256位的随机顺序(熵)。
2.提出SHA256哈希前几位,就可以创造一个随机序列的校验和。
3.把校验和加在随机顺序的后面。
4.把顺序分解成11位的不同集合,并用这些集合去和一个预先已经定义的2048个单词字典做对应。
5.生成一个12至24个词的助记码。
CS = ENT / 32
MS =(ENT + CS)/ 11
| ENT | CS | ENT + CS | MS |
- ------- + ---- + -------- + ------ +
| 128 | 4 | 132 | 12 |
| 160 | 5 | 165 | 15 |
| 192 | 6 | 198 | 18 |
| 224 | 7 | 231 | 21 |
| 256 | 8 | 264 | 24 |
助记词转化为种子
用户可能决定使用密码来保护他们的助记符。如果密码不存在,则使用空字符串“”代替。
为了从助记符创建二进制种子,我们使用带有用作密码的助记符句子(以UTF-8 NFKD表示)的PBKDF2函数和用作盐的字符串“助记符”+密码(再次以UTF-8 NFKD表示)。迭代计数设置为2048,HMAC-SHA512用作伪随机函数。派生密钥的长度为512位(64字节)。
这种种子可以在以后用于使用BIP-0032或类似方法生成确定性钱包。
种子的安全性
如果一个 HD 钱包助记词是 12 个单词,一共有 2048 个单词可能性,如何算出随机的生成的助记词可能性是一个排列问题,根据公式: n!/( n - r )! ,既 2048!/(2048-12)! = 5.2715379713014884760003093175282e+39。
我们可以举个类比,地球上的沙子数量在大约是1 后面 18 个零。如果你可以每秒生成 一百万个助记词,那么一年可以生成 1000000606024365=3.1536e+13,大约需要 1.6715937e+26 年遍历所有助记词
BIP32 分层确定性钱包
分层确定性钱包包含从树结构所生成的钥匙。这种母钥匙可以生成子钥匙的序列。这些子钥匙又可以衍生出孙钥匙,以此无穷类推。这个树结构表如下图所示。
从种子中创造HD钱包
HD钱包从单个root seed中创建,为128到256位的随机数。HD钱包的所有的确定性都衍生自这个根种子。任何兼容HD钱包的根种子也可重新创造整个HD钱包。所以简单的转移HD钱包的根种子就让HD钱包中所包含的成千上百万的密钥被复制,储存导出以及导入 这里的seed 就是根据BIP39 生成的改变索引可以让我们延长母密钥以及创造序列中的其他子密钥。比如子0,子1,子2等等。每一个母密钥可以右20亿个子密钥。
向密码树下一层重复这个过程,每个子密钥可以依次成为母密钥继续创造它自己的子密钥,直到无限代。
小记:seed 根基HMAC-SHA512 生成主私钥 称为m 和 主链编码 chain code
主私钥推导出主公钥M
扩展密钥
1.生成HD Wallets钱包的时候除了会生成主私钥(m)和主公钥(M),还会生成一个链码(chain code)。
2.利用master private key + chain code可以得到指定的子私钥(sub private key);
3.利用 master public key + chain code可以得到指定的子公钥(sub-public key);
4.为了方便起见,HD Wallets引入了extended的概念,以方便使用。即:
扩展型私钥extended private key包含了private key和chain code
扩展型公钥extended public key包含了public key 和 chain code
扩展密钥通过Base58Check来编码,从而能轻易地在不同的BIP0032-兼容钱包之间导入导出。扩展密钥编码用的Base58Check使用特殊的版本号,这导致在Base58编码字符中,出现前缀“xprv”和“xpub”。这种前缀可以让编码更易被识别。因为扩展密钥是512或者513位,所以它比我们之前所看到的Base58Check-encoded串更长一些。
私有子密钥
分层确定性钱包使用CKD(child key derivation)方程去从母密钥衍生出子密钥。
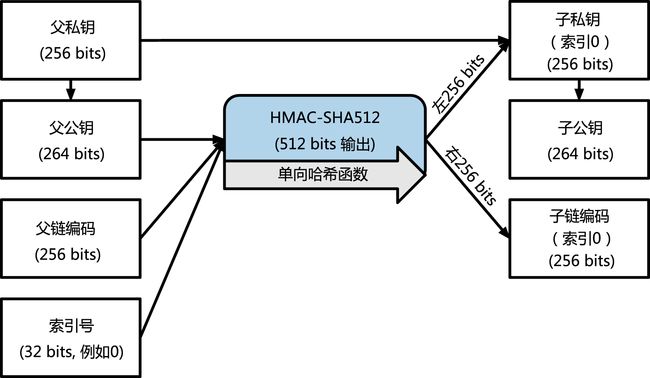
子密钥衍生方程是基于单项哈希方程。这个方程结合了:
• 一个母私钥或者公共钥匙(ECDSA未压缩键)
• 一个叫做链码(256 bits)的种子
• 一个索引号(32 bits)
链码是用来给这个过程引入看似的随机数据的,使得索引不能充分衍生其他的子密钥。因此,有了子密钥并不能让它发现自己的相似子密钥,除非你已经有了链码。最初的链码种子(在密码树的根部)是用随机数据构成的,随后链码从各自的母链码中衍生出来。
这三个项目相结合并散列可以生成子密钥,如下。
母公共钥匙——链码——以及索引号合并在一起并且用HMAC-SHA512方程散列之后可以产生512位的散列。所得的散列可被拆分为两部分。散列右半部分的256位产出可以给子链当链码。左半部分256位散列以及索引码被加载在母私钥上来衍生子私钥。在下中,我们看到这种这个说明——索引集被设为0去生产母密钥的第0个子密钥(第一个通过索引)。
子私钥不能从非确定性(随机)密钥中被区分出来。因为衍生方程是单向方程,所以子密钥不能被用来发现他们的母密钥。子密钥也不能用来发现他们的相同层级的姊妹密钥。如果你有第n个子密钥,你不能发现它前面的(第n-1)或者后面的子密钥(n+1)或者在同一顺序中的其他子密钥。只有母密钥以及链码才能得到所有的子密钥。没有子链码的话,子密钥也不能用来衍生出任何孙密钥。你需要同时有子密钥以及对应的链码才能创建一个新的分支来衍生出孙密钥。
公共子钥匙推导
正如之前提到的,分层确定性钱包的一个很有用的特点就是可以不通过私钥而直接从公共母钥匙派生出公共子钥匙的能力。这就给了我们两种去衍生子公共钥匙的方法:或者通过子私钥,再或者就是直接通过母公共钥匙。
那子私钥自己可被用做什么呢?它可以用来做公钥和比特币地址。之后它就可以被用那个地址来签署交易和支付任何东西。
因此,扩展的公共钥匙可以再HD钱包结构的分支中,被用来衍生所有的公钥(且只有公共钥匙)。
这种快捷方式可以用来创造非常保密的public-key-only配置。在配置中,服务器或者应用程序不管有没有私钥,都可以有扩展公共钥匙的副本。这种配置可以创造出无限数量的公共钥匙以及比特币地址。但是不可以花送到这个地址里的任何比特币。与此同时,在另一种更保险的服务器上,扩展私钥可以衍生出所有的对应的可签署交易以及花钱的私钥。
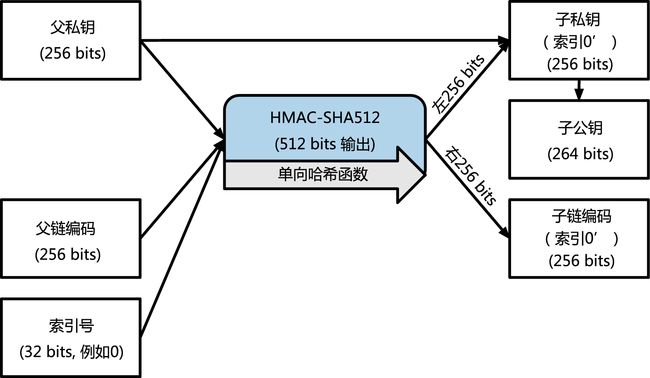
硬化子密钥的衍生
从扩展公共钥匙衍生一个分支公共钥匙的能力是很重要的,但牵扯一些风险。访问扩展公共钥匙并不能得到访问子私人密钥的途径。但是,因为扩展公共钥匙包含有链码,如果子私钥被知道或者被泄漏的话,链码就可以被用来衍生所有的其他子私钥。一个简单地泄露的私钥以及一个母链码,可以暴露所有的子密钥。更糟糕的是,子私钥与母链码可以用来推断母私钥。
为了应对这种风险,HD钱包使用一种叫做hardened derivation的替代衍生方程。这就“打破”了母公共钥匙以及子链码之间的关系。这个硬化衍生方程使用了母私钥去推到子链码,而不是母公共钥匙。这就在母/子顺序中创造了一道“防火墙”——有链码但并不能够用来推算子链码或者姊妹私钥。强化的衍生方程看起来几乎与一般的衍生的子私钥相同,不同的是是母私钥被用来输入散列方程中而不是母公共钥匙
当强化私钥衍生方程被使用时,得到的子私钥以及链码与使用一般衍生方程所得到的结果完全不同的。得到的密钥“分支”可以被用来生产不易被攻击的扩展公共钥匙,因为它所含的链码不能被用来开发或者暴露任何私钥。强化的衍生也因此被用来在上一层级,使用扩展公共钥匙的的密钥树中创造“间隙”。
简单地来说,如果你想要利用扩展公共钥匙的便捷来衍生公共钥匙的分支而不将你自己暴露在泄露扩展链码的风险下,你应该从强化母私钥,而不是一般的母私钥,来衍生公共钥匙。最好的方式是,为了避免了推到出主钥匙,主钥匙所衍生的第一层级的子钥匙最好使用强化衍生。
HD钱包密钥识别符(路径)
HD钱包中的密钥是用“路径”命名的,且每个级别之间用斜杠(/)字符来表示(见表4-8)。由主私钥衍生出的私钥起始以“m”打头。因此,第一个母密钥生成的子私钥是m/0。第一个公共钥匙是M/0。第一个子密钥的子密钥就是m/0/1,以此类推。
密钥的“祖先”是从右向左读,直到你达到了衍生出的它的主密钥。举个例子,标识符m/x/y/z描述的是子密钥m/x/y的第z个子密钥。而子密钥m/x/y又是m/x的第y个子密钥。m/x又是m的第x个子密钥。
HD path 密钥描述
m/0 从主私钥(m)衍生出的第一个(0)子密钥。
m/0/0 第一个私人子密钥(m/0)的子密钥。
m/0'/0 第一个子强化密钥first hardened child(m/0')的第一个常规子密钥。
m/1/0 第2个子密钥(m/1)的第一个常规子密钥
M/23/17/0/0 主密钥衍生出的第24个子密钥所衍生出的第17个子密钥的第一个子密钥所衍生出的第一个子密钥。
HD钱包树状结构的导航
HD钱包树状结构提供了极大的灵活性。每一个母扩展密钥有40已个子密钥:20亿个常规子密钥和20亿个强化子密钥。而每个子密钥又会有40亿个子密钥并且以此类推。只要你愿意,这个树结构可以无限类推到无穷代。但是,又由于有了这个灵活性,对无限的树状结构进行导航就变得异常困难。尤其是对于在不同的HD钱包之间进行转移交易,因为内部组织到内部分支以及亚分支的可能性是无穷的。
两个比特币改进建议(BIPs)提供了这个复杂问的解决办法——通过创建几个HD钱包树的提议标准。BIP0043提出使用第一个强化子索引作为特殊的标识符表示树状结构的“purpose”。基于BIP0043,HD钱包应该使用且只用第一层级的树的分支,而且有索引号码去识别结构并且有命名空间来定义剩余的树的目的地。举个例子,HD钱包只使用分支m/i'/是为了表明那个被索引号“i”定义的特殊为目地。
在BIP0043标准下,为了延长的那个特殊规范,BIP0044提议了多账户结构作为“purpose”。所有遵循BIP0044的HD钱包依据只使用树的第一个分支的要求而被定义:m/44'/。
BIP0044指定了包含5个预定义树状层级的结构:
m / purpose' / coin_type' / account' / change / address_index
第一层的目的地总是被设定为44'。第二层的“coin_type”特指密码货币硬币的种类并且允许多元货币HD钱包中的货币在第二个层级下有自己的亚树状结构。目前有三种货币被定义:Bitcoin is m/44'/0'、Bitcoin Testnet is m/44'/1',以及Litecoin is m/44'/2'。
树的第三层级是“account”,这可以允许使用者为了会计或者组织目的,而去再细分他们的钱包到独立的逻辑性亚账户。举个例子,一个HD钱包可能包含两个比特币“账户”:m/44'/0'/0' 和 m/44'/0'/1'。每个账户都是它自己亚树的根。
第四层级就是“change”。每一个HD钱包有两个亚树,一个是用来接收地址一个是用来创造找零地址。注意无论先前的层级是否使用是否使用强化衍生,这一层级使用的都是常规衍生。这是为了允许这一层级的树可以在可供不安全环境下,输出扩展的公共钥匙。被HD钱包衍生的可用的地址是第四层级的子级,就是第五层级的树的“address_index”。比如,第三个层级的主账户收到比特币支付的地址就是 M/44'/0'/0'/0/2。
HD 路径 主要描述
M/44'/0'/0'/0/2 第三个收到公共钥匙的主比特币账户
M/44'/0'/3'/1/14 第十五改变地址公钥的第四个比特币账户
m/44'/2'/0'/0/1 为了签署交易的在莱特币主账户的第二个私钥
总结:
- 通过Bip39 生成 seed 和 助记词
- Bip32 生成 主私钥 私钥 可以生成公钥
- 通过主私钥 或者 主公钥 可以推导子私钥 或者 子公钥 这里可以加上path
- Bip 44 给path加上含义
参考 http://zhibimo.com/read/wang-miao/mastering-bitcoin/Chapter04.html
参考https://github.com/bitcoin/bips/blob/master/bip-0039.mediawiki