20182301 2019-2020-1 《数据结构与面向对象程序设计》实验7报告
课程:《程序设计与数据结构》
班级: 1823
姓名: 赵沛凝
学号:20182301
实验教师:王志强
实验日期:2019年11月1日
必修/选修: 必修
1.实验内容
- 定义一个Searching和Sorting类,并在类中实现linearSearch,SelectionSort方法,最后完成测试。要求不少于10个测试用例,提交测试用例设计情况(正常,异常,边界,正序,逆序),用例数据中要包含自己学号的后四位,提交运行结果图。
- 重构你的代码
把Sorting.java Searching.java放入 cn.edu.besti.cs1823.(姓名首字母+四位学号) 包中(例如:cn.edu.besti.cs1823.G2301)把测试代码放test包中,重新编译,运行代码,提交编译,运行的截图(IDEA,命令行两种) - 参考http://www.cnblogs.com/maybe2030/p/4715035.html ,学习各种查找算法并在Searching中补充查找算法并测试,提交运行结果截图
- 补充实现课上讲过的排序方法:希尔排序,堆排序,二叉树排序等(至少3个)
测试实现的算法(正常,异常,边界),提交运行结果截图(如果编写多个排序算法,即使其中三个排序程序有瑕疵,也可以酌情得满分) - 编写Android程序对实现各种查找与排序算法进行测试,提交运行结果截图,推送代码到码云(选做,加分)
2. 实验过程及结果
第一个:
- 第一个实验比较简单,只要写出linearSearch,SelectionSort方法,这两种方法在前面都有涉及,代码如下:
- SelectionSort方法
public static void selectionSort(Comparable[] data) {
int min;
for(int index=0;index- linearSearch方法
public static Comparable linearSearch(Comparable[] data,Comparable target){
Comparable result = null;
int index = 0;
while(result == null && index < data.length){
if(data[index].compareTo(target)==0)
result = data[index];
index++;
}
return result;
}- 这两个方法用于测试时只需要获取一个关键词,first、last、telephone,代码如下:
player[0] = new Contact("d", "j", "2301");
Contact target1 = new Contact("","","0505");
Contact found[] = new Contact[10];
found[0] = (Contact) Searching.linearSearch(player,target1);
- 最后,判断是否找到
for(int i=0;i<8;i++){
System.out.println("Test"+(i+1)+":");
if(found[i] == null)
System.out.println("Player was not found.");
else
System.out.println("Found: "+ found[i]);
}第二个
- 第二个更加简单,第一步主要理解方法重构
- 重构就是通过调整程序代码,但并不改变程序的功能特征,达到改善软件的质量、性能,使程序的设计模式和架构更趋合理,更容易被理解,提高软件的扩展性和维护性。
- 第二步复习命令行
- 详细命令行介绍见链接二
- 在使用命令行的时候,出现了问题,详见问题3.
第三个
- 首先学习查找算法,并进行代码实现,如下:
- linearSearch
public static int linearSearch(int[] data,int target){
int result = 0;
int index = 0;
while(result == 0 && index < data.length){
if(data[index]==target)
result = data[index];
index++;
}
return result;
}- InsertionSearch
public static int InsertionSearch(int[] a, int x , int left, int right){
if(xa[a.length-1]){ //不加这句会抛出异常,若找的数不在范围内,则mid可能越界//
return -1; }
int mid = left + (x-a[left])/(a[right]-a[left])*(right-left);
if(left>right){
return -1; }
if(xa[mid]){
return InsertionSearch(a,x,mid+1,right);
} else{
return a[mid];
}
} - FibonacInsearch
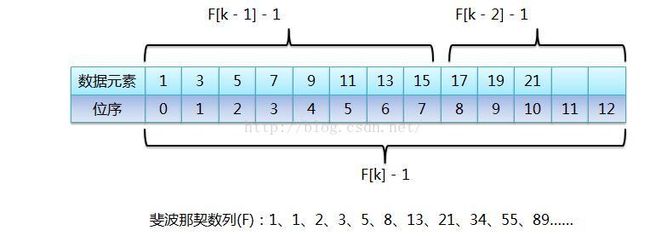
- 斐波那契查找就是在二分查找的基础上根据斐波那契数列进行分割的。在斐波那契数列找一个等于略大于查找表中元素个数的数F[n],将原查找表扩展为长度为Fn,完成后进行斐波那契分割,即F[n]个元素分割为前半部分F[n-1]个元素,后半部分F[n-2]个元素,找出要查找的元素在那一部分并递归,直到找到。详细了解斐波那契查找见链接3
public static void fibonacci(int[] f){
f[0]=0;
f[1]=1;
for(int i=2;if[k]-1){
k++;
}
int[] tmp = new int[f[k]-1];
System.arraycopy(a,0,tmp,0,a.length);//拷贝a元素到tmp中
for(int i=a.length;ia[mid]){
left=mid+1;
k-=2;
}
else{
if(mid - 二叉树查找
- 在二叉树查找时,进行传参时遇到了一个问题,见问题二。
//二叉树查找
private static Node root;
private Node temp;
public Searching2() {
root = null;
}
public void add(int data1) {//向二叉树插入元素
if (this.root == null) {
root = new Node(data1);
temp = root;//存下第一个节点
} else {
addW(root,data1);
}
}
public void addW(Node x,int data1) {//判定插入元素的位置
//当数据大于等于节点时,放右子树
if (data1 >= x.getData()) {
if (x.getRight() == null) {
x.setRight(new Node(data1));
} else {
addW(x.getRight(),data1);
}
}
else {//数据小于节点时,放左子树
if (x.getLeft() == null) {
x.setLeft(new Node(data1));
} else {
this.addW(x.getLeft(),data1);
}
}
}
public void print() {
root.print(); System.out.println();
}
public Node BSTreesearch(Node x,int data2) {//在二叉树中寻找元素
if(x==null)
return null;
if(data2==x.getData()){
return x;
}
else if(data2- 分块查找
public static int blocksearch(int[] index,int[] data,int target,int m){
int i = Bsearch(index,target);
System.out.println("在第"+i+"块");
if(i>=0){
int j = m*i;
int k = m*(i+1);
for(;j- 哈希查找
public static int[] addhashlinear(int[] data){
int[] result=new int[13];
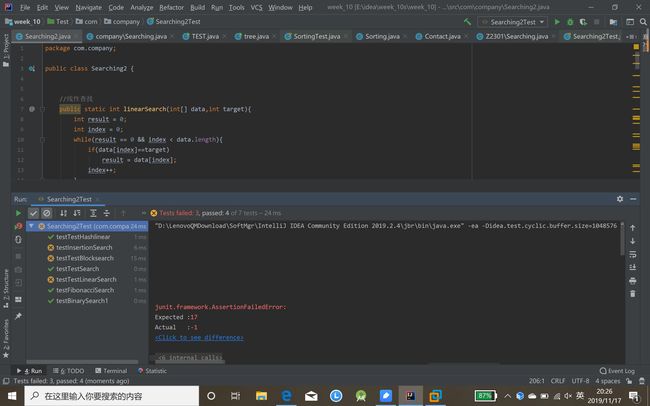
for(int i=0;i- 以上查找算法均正确,在测试中可检验出通过or错误,如图:
实验四
- 复习上课讲的排序方法并进行测试,代码如下:
- 希尔排序
public class shell {
public static void main(String[] args){
int gap,a,d,count=0,temp,l,okk;
int[] c=new int[10];
Arrays.fill(c,0);
String e,ok="";
Scanner scan=new Scanner(System.in);
System.out.println("输入数组数字:(空格隔开)");
e=scan.nextLine();
String[] f=e.split(" ");
count=f.length;
for(a=0;a0;gap=gap/2){
for(d=gap;d<=f.length-1;d++){
l=d;
temp=c[l];
if(c[l]=0&&temp - 堆排序
public class dui {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int a, b, c, d, dd,head, kk, temp, i = 1;
String e;
System.out.println("请输入堆元素(以空格隔开)");
e = scan.nextLine();
String[] f = e.split(" ");
int[] count = new int[f.length];
// int[] fin=new int[f.length];
//以数组形式构造树
for (a = 0; a < f.length; a++) {
count[a] = Integer.parseInt(f[a]);
}
kk = count.length;//待排序的元素个数
String pp="";
for(int oo=0;oo= 3) {
temp = kk;
i=1;
while (temp > 1) {
c = temp / 2 - 1;
if (c==-1)
c=0;
if (i == 1) {
if (kk % 2 == 0) {
if (count[c * 2 + 1] > count[c]) {
int kkk = count[c];
count[c] = count[c * 2 + 1];
count[c * 2 + 1] = kkk;
}
}
if (kk % 2 != 0) {
if (count[c * 2 + 1] > count[c * 2 + 2] && count[c * 2 + 1] > count[c]) {
int kkk = count[c];
count[c] = count[c * 2 + 1];
count[c * 2 + 1] = kkk;
} else if (count[c * 2 + 2] > count[c * 2 + 1] && count[c * 2 + 2] > count[c]) {
int kkk = count[c];
count[c] = count[c * 2 + 2];
count[c * 2 + 2] = kkk;
}
}
} else {
if (count[c * 2 + 1] > count[c] || count[c * 2 + 2] > count[c]) {
if (count[c * 2 + 1] > count[c * 2 + 2]) {
int kkk = count[c];
count[c] = count[c * 2 + 1];
count[c * 2 + 1] = kkk;
} else {
int kkk = count[c];
count[c] = count[c * 2 + 2];
count[c * 2 + 2] = kkk;
}
}
}
temp--;
i++;
}
b = count[0];
count[0] = count[kk - 1];
count[kk - 1] = b;
kk--;
i++;
}
for(d=0;d<3;d++){
for(dd=d;dd<3;dd++){
if(count[dd] - 二叉树排序
public class tree {
public static void main(String[] args){
int a,b,c,d,count;
int[] h=new int[10];
Arrays.fill(h,0);
leaf root=null;
String f,g;
Scanner scan=new Scanner(System.in);
System.out.println("请输入数组数字(空格隔开)");
f=scan.nextLine();
String[] e=f.split(" ");
for(c=0;c current.root) {
if(current.right==null) {current.right=temp; break;}
else current=current.right;
}
if(temp.root 第五个
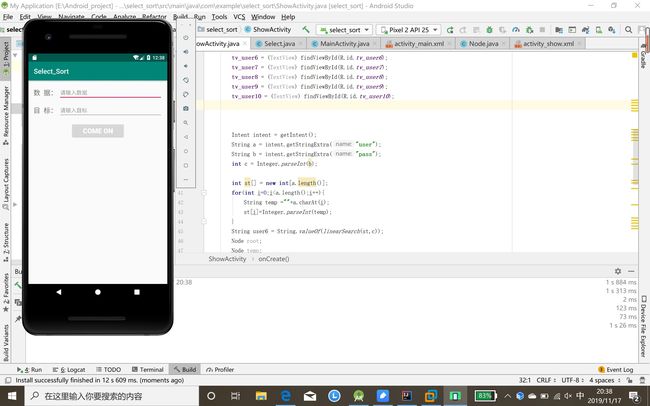
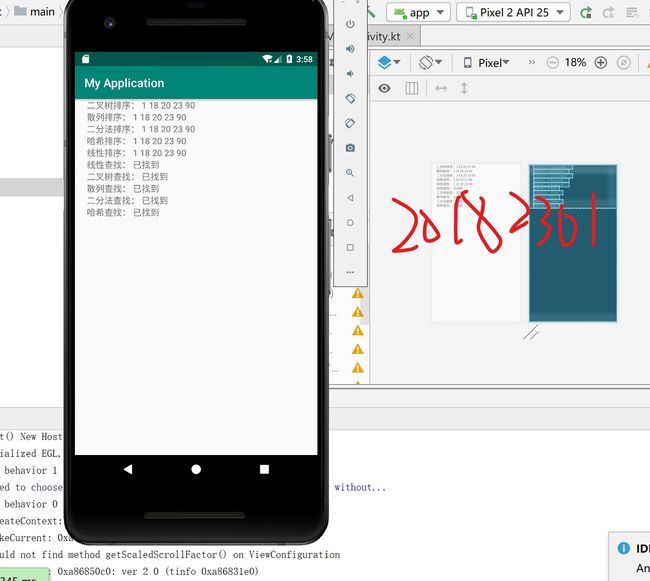
- Android重点在于接口问题,搞清楚后就迎刃而解啦
3. 实验过程中遇到的问题和解决过程
- 问题1:为什么要进行代码重构?重构可以到达的目标是什么?何时需要代码重构?重构的方法是什么?
- 问题1解决方案:
- 为什么要进行代码重构?
- 需求的不断变更是重构的最根本原因,而且重构是每一个开发人员都要面对的功课。
- 代码架构最初的设计也是经过精心的设计,具有良好架构的。但是随着时间的推移、需求的剧增,必须不断的修改原有的功能、追加新的功能,还免不了有一些缺陷需要修改。为了实现变更,不可避免的要违反最初的设计构架。经过一段时间以后,软件的架构就千疮百孔了。bug越来越多,越来越难维护,新的需求越来越难实现,最初的代码构架对新的需求渐渐的失去支持能力,而是成为一种制约。最后新需求的开发成本会超过开发一个新的软件的成本,这就使这个app的生命走到了尽头。
- 代码重构就能够最大限度的避免这样一种现象。系统发展到一定阶段后,使用重构的方式,不改变系统的外部功能,只对内部的结构进行重新的整理。通过重构,不断的调整系统的结构,使系统对于需求的变更始终具有较强的适应能力。
- 重构可以到达的目标是什么?
- 持续偏纠和改进软件设计
- 使代码更被其他人所理解
- 帮助发现隐藏的代码缺陷
- 从长远来看,有助于提高编程效率,增加项目进度(进度是质量的敌人,质量是进度的朋友)
- 何时需要代码重构?
- 模糊的不具有任何意义的方法名。
- 臃肿的类
- 长方法
- 大量的传参
- 现有的代码对它要实现的功能显得过于复杂,并且你分析过它。
- 修改后的代码远比现存的代码逻辑要清晰。
- 有足够的时间,人手,财力来支持对项目进行回归测试。
- 现有的代码陈旧无效率。
- 无人认领的,写的很烂的代码都属于此类。
- 代码禁区。这部分代码只有一个人可以修改,而且修改可能带来更大的隐患。
- 重构的方法是什么?
- 提取类/抽离方法
- 像“臃肿的类”(xmppmanager.h)这种代码臭味应该将原有类中的方法和属性移动到适当数目的新类中去。旧类中对应新类的方法和属性应该被移除。另外,有时候一些类过于臃肿是因为它包含了被其他类使用本应该是其他类的成员方法的成员方法。这些方法也应该被迁移到合适的类中。
- 分离条件
- 许多时候,一个方法很长是因为包含好几个分支语句(if-else)。这些分支条件可以被提取和移动到几个单独的方法中。这确实能大大改善代码可读性和可理解性。
- 引入参数对象/保留全局对象
- 好几个参数被传入方法。问题主要与需要从已有方法中增加或者移除一个方法参数有关。在这种场景,建议将相关方法参数组成一个对象(引入参数对象),让方法传递这些对象而不是每个单独的参数。
- 用符号常量替换无意义数字
- 对于有意义的并且到处被使用的字面常量,应该为它们分配一个命名常量。这能大大增强代码可读性和可理解性。
- 重命名方法
- 正如上面提到的,模糊不清的方法名会影响代码的可使用性有些模糊不清的名称应该重命名为有意义的可能与业务术语有关的名称,来帮助开发者通过业务上下文更好地理解代码。
- 内存优化
- 检查工程的内存使用情况,及时Release。
- 去除硬编码,将文案统一至模块化的宏定义文件
- 将一些通过的文案,常用的文案统一便写到宏定义文件
- 提取类/抽离方法
- 问题2:按照原本的二叉树查找代码,难以将root整个树的根传过去,并进行递归,于是新写了一个方法,如下:
- 问题2解决方案:
public int BS(int target){
Node k =BSTreesearch(root,target);
int po = k.getData();
return po;
}- 相对应的测试代码
@Test
public void testTestSearch() {
Node root;
Node temp;
int[] number = new int[]{20,18,23,1,9,10};
Searching2 tree = new Searching2();
for(int m=0;m最后测试成功
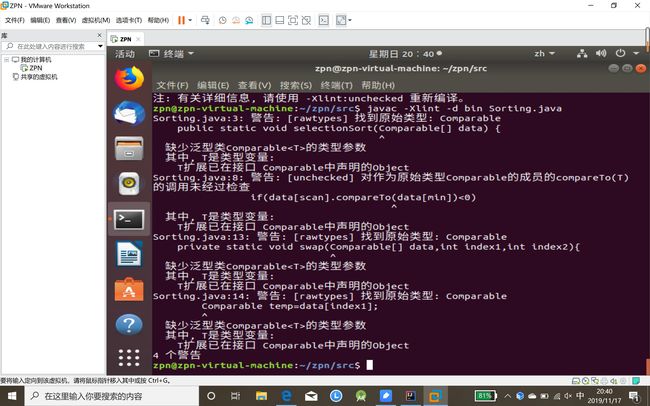
问题3:在使用虚拟机的命令行代码时,出现了如下问题:
- 问题3解决方法:
- 因为使用集合时没有定义泛型,这不是错误,只是警告,不影响使用,如果使用泛型就不报那个警告了。jdk1.5以后再定义容器的时候要加上泛型
- 解决方案有三个,如图:
其他(感悟、思考等)
本次实现较为简单,基本上是复习老师上课讲的内容,以后自己也要多多复习。
参考资料
- 代码重构意义和方法
- Linux命令大全
- FibonacInsearch