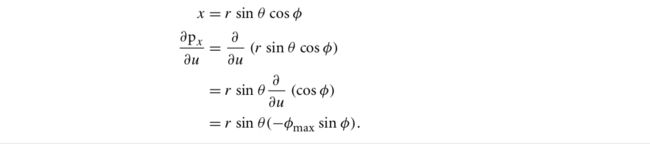3.1 Base Shape Interface(基本图形接口)
pbrt中所有的图形都继承自一个基类class Shape,它的代码简略如下:
class Shape {
public:
Shape(const Transform *ObjectToWorld, const Transform *WorldToObject,
bool reverseOrientation);
virtual ~Shape();
virtual Bounds3f ObjectBound() const = 0;
virtual Bounds3f WorldBound() const;
virtual bool Intersect(const Ray &ray, Float *tHit,
SurfaceInteraction *isect,
bool testAlphaTexture = true) const = 0;
// Shape Public Data
const Transform *ObjectToWorld, *WorldToObject;
const bool reverseOrientation;
const bool transformSwapsHandedness;
};
可以看到它的主要两个成员变量ObjectToWorld和WorldToObject,因为pbrt中所有的图形都是定义在物体坐标系(object coordinate space)的,例如所有的圆形的中点都在它自身物体坐标系的原点,ObjectToWorld和WorldToObject这两个变换用来实现物体坐标系到世界坐标系的转换。
另外两个成员reverseOrientation和transformSwapsHandedness感觉用的不多,先忽略。
还有一点需要注意的是所有的shapes存储的transformations都是指针,而不是具体的对象。因为pbrt中有一个Transforms的对象池,详见2.7节。
3.1.1 Bounding(边界)
因为在渲染中许多对象的计算是很耗时的,如果有一个3D立方体(也就是第二章的包围盒)可以正好包住它,如果一条光线并没有经过这个包围盒,那就可以避免对这个对象进行昂贵的计算了。
一个和坐标轴对齐的包围盒只需要6个浮点型的内存(两个对角线的点),并且计算一条射线和包围盒是否相交是几乎不耗时的操作。因此每个Shape的实现都必须实现返回它自身包围盒的接口。也就是上面代码块中的ObjectBound()和WorldBound()。
ObjectBound()返回的是物体空间的包围盒,WorldBound()返回的是世界坐标系的包围盒。pbrt提供了一个默认的WorldBound()的方法,就是先计算物体坐标系下的包围盒,再变换到世界坐标系下。如下:
Bounds3f Shape::WorldBound() const {
return (*ObjectToWorld)(ObjectBound());
}
但许多Shapes可以根据自身的特点计算出更小更紧凑的包围盒。如下图的一个例子:
图a是先计算在物体空间中计算出包围盒,然后把包围盒变换到世界坐标系(图a的实线矩形),但是变换到世界坐标系后的矩形已经不是坐标轴对齐了,实际上它的包围盒是虚线的正方形(太大了不紧凑,不好)。而图b中,先把三角形变换到世界坐标系,然后计算它的包围盒,这样的包围盒就比图a的紧凑多了。
3.1.2 Ray-Bounds Intersections(光线-边界相交)
Shape的具体实现必须要提供一个(有可能两个)方法来测试光线和shape的交点。第一个是Shape::Intersect(),接口长这个样子,它返回第一个交点的几何信息:
virtual bool Intersect(const Ray &ray, Float *tHit,
SurfaceInteraction *isect, bool testAlphaTexture = true) const = 0;
还有几点要注意的:
1.Ray结构体中国有tMax成员变量,对应的是ray的终点,交点程序必须忽略在终点后面的交点。
2.如果发现一个交点,该交点和光线起点的距离将存储到tHit指针指向的数据中,如果沿着ray有多个交点,则tHit记录的是最近的一个。
3.交点的信息存储在SurfaceInteraction结构体中,它完整记录一个表面的几何属性。这个class在整个pbrt中用的非常多,它让光线跟踪器的几何部分彻底从着色和光照部分独立出来。
4.传递到intersection routines的rays是在世界坐标系中,因此shapes需要在intersection tests之前先把他们转换到物体坐标系中。返回的交点信息应该在世界坐标系中。
另一个intersection test method是Shape::IntersectP(),它只是检查是否相交,而不会返回交点的详细信息...
3.1.4 Surface Area和3.1.5 Sideness略过。
3.2 Spheres(球)
球面是一种特殊的二次曲面,二次曲面是用x,y,z二次多项式描述的表面。球面是最简单的一种曲面,很适合作为光线跟踪器学习的起点。pbrt工程中支持六种曲面:球,圆锥,碟形(一种特殊的圆锥),圆柱,双曲面,抛物面。
许多表面有两种描述的方式:隐式形式(implicit form)和参数形式(parametric form)。一个描述3D表面的隐式函数为:
所有满足这个条件的点就组成这个表面。对于一个中心在原点的单位球体,它的隐式方程就是x2+y2+z2 - 1 = 0.
许多表面也用参数形式来用2D点映射3D表面的点。例如,对于一个半径r的球体,可以用一个2D球面坐标(θ , φ),其中θ范围从0到π ,φ从0到2π:
如下图(截了第5章的一个图,书中在此处没有好的图展示)
我们可以将函数f (θ , φ)转换到一个范围为[0, 1]2的函数f (u, v)(这实际上就是纹理坐标!),也可以通过限制θ和φ的范围来产生一个局部球体,只需要θ ∈ [θmin, θmax]和φ ∈ [0, φmax],
下图展示了一个纹理贴图,左边的纹理贴满了整个球,右边的只贴了球的局部(u的(0 ~ 1)对应φ的(0 ~ φmax), v的(0 ~ 1)对应θ的(θmin ~ θmax))。
下面看下Sphere Class的构造函数和成员变量,它继承Shape Class,简单看下它的代码:
class Sphere : public Shape {
public:
// Sphere Public Methods
Sphere(const Transform *ObjectToWorld, const Transform *WorldToObject,
bool reverseOrientation, Float radius, Float zMin, Float zMax,
Float phiMax)
//省了...
private:
// Sphere Private Data
const Float radius;
const Float zMin, zMax;
const Float thetaMin, thetaMax, phiMax;
};
从构造函数的参数和成员变量可以看出,这些都是构造一个球面(或局部球面)的必要参数,比较简单略过不提。
3.2.2 Intersection Tests(相交测试)
首先看下球面相交测试的接口,如下:
bool Sphere::Intersect(const Ray &r, Float *tHit, SurfaceInteraction *isect,
bool testAlphaTexture) const {
//省略...
}
返回值表示球和光线是否有交点,如果有交点,则会返回对应ray的t值(tHit),以及交点的表面的信息(SurfaceInteraction),testAlphaTexture参数还不知道干嘛的,先忽略。
ray和球面的相交测试因为球的中心位于原点而变得较简单。但前提是先要把ray先转换到球的物体坐标系中。代码如下:
Ray ray = (*WorldToObject)(r, &oErr, &dErr);
代码中的oErr和dErr是变换计算产生的误差,具体可以看3.9节的浮点型算法(自己看了下感觉挺复杂的有时间再研究吧...)。
接下来,因为中心在原点,半径为r的球的隐式表达式为:
而ray的公式为
将光线公式代入球面公式,得到
除了t之外其他系数都是已知的。我们展开公式,并将这些系数归纳,这是一个关于t的二次方程,
其中
求解这个二次方程,自己推算了一波(十几年没解过方程了...)
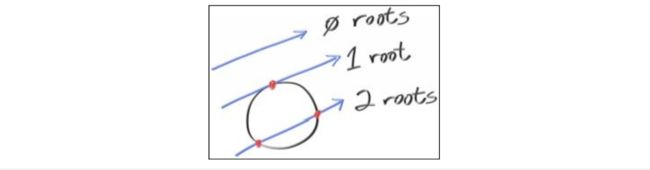
结果有三种可能,无解,一个解,两个解,对应ray和球不相交,相切,有两个交点,如下图(出自《Ray Tracing in One Weekend》)
pbrt工程中用Quadratic()工具函数来解二元一次方程,注意它忽略了相切的情况(可能是考虑浮点型计算结果等于0.0的机会极少吧),若不想交则返回false,若相交则返回两个交点对应的t0和t1值,且t0小于t1。
得到t0和t1后,还要考虑许多的细节,主要是ray自身的t的范围是[0,tmax],还有如果是局部球面,还要另外计算,这个书中有详述,这里不写了。
得到交点后,继续就出对应的u,v值,略过不提。
下面是求在交点处表面的一些重要信息,并利用它们构造SurfaceInteraction对象返回。主要有该交点的表面偏导数 ∂p/∂u, ∂p/∂v,和法线偏导数∂n/∂u,∂n/∂v。偏导数,也可以说是变化率,比如
∂p/∂u实际上就是点p在u方向上的变化率,但是要注意的是其实p和u分别是在不同的空间坐标中的,p是在球面自身的物体空间,是3D空间,而uv实际上在范围[0,1]的2D纹理空间,如下图:
可以把p对u的变化率理解为p在球面的纬度方向上的变化率,v对应是经度方向。p是一个向量,即p(px, py, pz),很容易可以知道在纬度方向z坐标是无变化的,因此∂pz/∂u为0。另外书中以∂px/∂u为例推导了如何求解.我直接截了书上的图:
经过化简和咕嘟咕嘟...,最后得到
3.2.3 法线向量的偏导数
法线向量的偏导数∂n/∂u,∂n/∂v的求法过程就复杂多了,该怂的时候就要怂,跳过就好,需要就直接抄公式。
后面的3.3~3.5节讲 圆柱,碟形,圆锥,双曲面等其他图形接口,与球面类似,不再记录。
下面重点记录下三角形。
3.6 三角形网格
在计算机图形学中,三角形是用的最多的图形。。复杂的场景可以用成千上万的三角形来建模,来展现很好的细节效果。如下图的模型包含了400万个三角形。
通常为了高效使用内存,会将整个三角形网格的顶点存放在一个数组里,并使用另一个数组存放每个三角形的顶点偏移。
对于比较紧凑的三角形网格,顶点和面的数量关系可以近似认为是(书中使用欧拉-庞加莱方程来证明,不过我没怎么看懂...)
也就是说,顶点是数量约等于面的数量的两倍。因为每个面和三个顶点关联,所有顶点总共会(平均)被关联6次(想象一下6个三角形组成一个正六边形,六边形的中心)。因此,当顶点被共享时,分摊下来每个三角形需要12个字节来存储偏移值(3个 4字节的32位整型),加上一个顶点大小的一半也就是6个字节(,假设一个顶点是由3个4字节的浮点型组成,也就是一个顶点原本需要12个字节)--也就是每个三角形占18个字节。而如果是直接存储顶点,那需要36个字节。当存在表面法线和纹理坐标时,这种方式的效果将更好。
TriangleMesh class的代码简略如下:
struct TriangleMesh {
// TriangleMesh Public Methods
TriangleMesh(const Transform &ObjectToWorld, int nTriangles,
const int *vertexIndices, int nVertices, const Point3f *P,
const Vector3f *S, const Normal3f *N, const Point2f *uv,
const std::shared_ptr> &alphaMask,
const std::shared_ptr> &shadowAlphaMask,
const int *faceIndices);
// TriangleMesh Data
const int nTriangles, nVertices; //三角形数量,顶点数量
std::vector vertexIndices; //索引(偏移值)数组
std::unique_ptr p; //顶点数组
std::unique_ptr n; //法线数组
std::unique_ptr s; //切线数组
std::unique_ptr uv; //uv数组
std::shared_ptr> alphaMask, shadowAlphaMask; //还没用过,估计是用来做如半透明,阴影等效果的mask
std::vector faceIndices; //面的索引
};
看到这个类想必熟悉图形API的接口的人都会觉得很眼熟,就是我们用opengl画三角形时都会定义的数组啊!
3.6.1 三角形
Triangle class也实现Shape接口。它代表一个单一的三角形。看下它的成员变量:
class Triangle : public Shape {
public:
//省略...
private:
// Triangle Private Data
std::shared_ptr mesh;
const int *v;
int faceIndex;
};
如代码所示,Triangle存储很少的数据--只有一个指向含有该三角形的TriangleMesh的指针,以及一个指向它的三个顶点索引的指针。从它的构造函数可以看出:
Triangle(const Transform *ObjectToWorld, const Transform *WorldToObject,
bool reverseOrientation,
const std::shared_ptr &mesh, int triNumber)
: Shape(ObjectToWorld, WorldToObject, reverseOrientation),
mesh(mesh) {
v = &mesh->vertexIndices[3 * triNumber];
}
需要注意的是v是一个指向顶点索引的指针.
接下来讲了CreateTriangleMesh(), ObjectBound(),WorldBound()等接口,较简单不记录了。
3.6.2 三角形的Intersection
三角形的相交测试也是实现Shape的Intersect接口,如下:
bool Triangle::Intersect(const Ray &ray, Float *tHit,
SurfaceInteraction *isect, bool testAlphaTexture) const {
//略...
}
在pbrt中三角形和ray的相交测试方法比较有意思,首先将当前世界空间坐标变换到一个另一个特殊空间坐标(暂且叫相交坐标),在该坐标下,ray的起点位于原点,ray的方向指向+z方向。三角形的顶点也变换到相交坐标下,然后再进行相交测试。这样相交测试会更加简单,例如,交点的x和y坐标必定为0。另外的优势在3.9.3节中提到(还没研究)。
计算世界坐标到相交坐标具体有三步:平移T,置换P,和切变S。具体实现没有将三个变换分别求出再计算他们的聚合变换矩阵M=SPT, 而是在每一步直接变换顶点,这样更加高效。
首先看第一步,T矩阵很容易得出
我们将这个变换作用到三角形的三个顶点,代码如下:
// Translate vertices based on ray origin
Point3f p0t = p0 - Vector3f(ray.o);
Point3f p1t = p1 - Vector3f(ray.o);
Point3f p2t = p2 - Vector3f(ray.o);
第二步,将ray的方向向量的绝对值最大的一个维度,作为变换后的z轴。另外的两个维度则随意放置到变换后的x轴和y轴。这样可以确保变换后+z轴方向一定是非0的。
例如,如果ray的方向最大的维度是x轴,那么置换矩阵为:
这样看起来不够明显,可以把它和一个向量相乘
这样可以看出,这个置换矩阵的作用其实就是把dx,dy,dz交换了下位置,dx最大因此它被放在了z轴的位置。下面是代码:
// Permute components of triangle vertices and ray direction
int kz = MaxDimension(Abs(ray.d));
int kx = kz + 1;
if (kx == 3) kx = 0;
int ky = kx + 1;
if (ky == 3) ky = 0;
Vector3f d = Permute(ray.d, kx, ky, kz);
p0t = Permute(p0t, kx, ky, kz);
p1t = Permute(p1t, kx, ky, kz);
p2t = Permute(p2t, kx, ky, kz);
第三部,用一个切变矩阵把ray变换到+z轴上:
要看到它的效果最好的方法就是将它和方向向量相乘,你会神奇的发现结果就是[0, 0, 1, 0] !
现在,只把三角形顶点的x和y坐标切变,我们可以等到判断完是否相交后,再把顶点的z坐标切变(因为判断相交不需要顶点的z坐标)。代码如下:
// Apply shear transformation to translated vertex positions
Float Sx = -d.x / d.z;
Float Sy = -d.y / d.z;
Float Sz = 1.f / d.z;
p0t.x += Sx * p0t.z;
p0t.y += Sy * p0t.z;
p1t.x += Sx * p1t.z;
p1t.y += Sy * p1t.z;
p2t.x += Sx * p2t.z;
p2t.y += Sy * p2t.z;
接下来的任务就是ray从原点出发,沿着+z方向,看它是否和变换后的三角形相交。这个问题等同于一个2D问题,也就是只考虑xy坐标就行,判断(0,0)是否处在三角形三个顶点的xy坐标之内。如下图:
为了理解相交算法如何工作,首先回忆2.5节中,两个向量的叉乘得出以它们为边的平行四边形的面积。在2D中,向量a和b,面积就是
三角形的面积是它的一般。因此,在2D中,顶点为p0,p1,p2的三角形的面积是(原书的公式有点小错误)
应该注意到,叉乘的结果是有正负符号的,也就是说得出平行四边形或三角形的面积都是有符号的。如下图:
p0和p1是三角形的两个顶点,如果第三个顶点在向量p0p1的左边,那三角形的面积就为正,在右边则为负。我们可以用这个三角形面积特性定义一个有符号边界函数(a signed edge function),假设第三个点是p,那么这个signed edge function为:
通过这个特性,如果一个点对于三角形的三个边的edge function的值的符号都相同,那么说明该点相对三条边都在同一侧(注意三条边是向量,并且是首尾相连的向量),那么必定处于三角形的内部。
多亏前面的坐标转换,我们要测试的点p是(0, 0),因此可以简化公式,对于一条edge系数e0,有:
同理可以算出e1,e2.代码如下:
// Compute edge function coefficients _e0_, _e1_, and _e2_
Float e0 = p1t.x * p2t.y - p1t.y * p2t.x;
Float e1 = p2t.x * p0t.y - p2t.y * p0t.x;
Float e2 = p0t.x * p1t.y - p0t.y * p1t.x;
得到三个edge function的值后,第一步,我们首先判断这三个值的符号是否相同,若不同则表示没有交点;第二步,如果这三个值的和为0,说明ray非常接近三角形的边缘,我们也认为是没有交点。代码如下:
// Perform triangle edge and determinant tests
if ((e0 < 0 || e1 < 0 || e2 < 0) && (e0 > 0 || e1 > 0 || e2 > 0))
return false;
Float det = e0 + e1 + e2;
if (det == 0) return false;
接下来考虑如何求ray的t值。因为ray是从原点开始,是单位长度,且是沿着+z轴,因此交点的z坐标的值正好等于参数值t!为了求交点的z值,首先需要把三角形的三个顶点的z值进行切变变换(上面还没做)。然后,利用重心坐标对三个顶点进行插值就可以求得交点的z值。这些重心坐标如下:
这个插值z由下式得到:
代码如下:
// Compute scaled hit distance to triangle and test against ray $t$ range
p0t.z *= Sz;
p1t.z *= Sz;
p2t.z *= Sz;
Float tScaled = e0 * p0t.z + e1 * p1t.z + e2 * p2t.z;
if (det < 0 && (tScaled >= 0 || tScaled < ray.tMax * det))
return false;
else if (det > 0 && (tScaled <= 0 || tScaled > ray.tMax * det))
return false;
// Compute barycentric coordinates and $t$ value for triangle intersection
Float invDet = 1 / det;
Float b0 = e0 * invDet;
Float b1 = e1 * invDet;
Float b2 = e2 * invDet;
Float t = tScaled * invDet;
(重心坐标系的知识可以参看《Fundamentals of Computer Graphics》第2章相关章节)
最后求讲下∂p/∂u 和 ∂p/∂v,因为三角形是平面,所以只要给定了三角形在3D世界坐标系的顶点坐标和在2D uv坐标系上的uv坐标,所有对于三角形平面上的所有点,∂p/∂u 和 ∂p/∂v都是一样的。直接截了书上的求解过程:
因为考虑许多误差的细节,所以代码会比公式稍复杂,不再记录了,需要再直接看书吧。