理性关卡设计手册：如使用RLD理论指导游戏关卡开发？

前言

作为本系列的开篇(理性设计手册系列)，本篇的内容对于理性关卡设计理论来说，具有着极为重要的意义，请耐心阅读 --编译者Katana

作者：卢克·麦克米兰（Luke McMillan）

设计是高度个人化的一项工作-我对此没有任何异议，并且我已经看到许多独特且多样化的设计方法。过去困扰我的是看起来像某种围绕着有效设计实践的神秘主义。"禅系”（Zen）设计理念来源于音乐创作的背景之下，规则和启发占据了主导地位。这对我而言却并不适用，尤其是当你考虑到这些“胡说八道”的理论将可能带来相关的财务风险时，Dan Cook，Raph Koster，Joris Dormins，Steve Swink，Ernest Adams和Jesse Schell（仅举几例！）已经在将“炼金术”转变为科学理论的道路上取得了重大进展。这种理解游戏的新方法，其分支之一是Rational Design(即理性设计)或者Rational Level Design [RLD]。我以前在这里写过一些关于这个概念的文章，但是从一开始我并没有公开地发表过任何文章。

我本来最初的目的是把这一切理论都整合编写成免费开源的教科书，命名为“ The Rational Designers Handbook”(即理性设计师手册)。后来我改变了主意，决定将自己的工作手册变成一系列在Gamasutra上的博客文章。这样，我可以让其他的游戏开发者、学者和教育工作者自行选择、共同创作。因此，这里是理性设计师手册的第一部分-导论。

什么是理性的关卡设计(The Rational Level Design) / RLD？

理性关卡设计（RLD）是一种客观地量化用户体验元素的方法，目的是创造一致的游戏体验。RLD最常用于理解各种游戏元素如何影响难度。由于难度在确定用户体验中起着重要作用（愤怒和无聊之间的不稳定平衡！），因此我们可以使用RLD中的目标——数字驱动系统来打造用户体验。虽然RLD现在不仅仅用于创建游戏关卡，但RLD标签已经被定义，被用来描述使用这种数据驱动方法的设计活动。

我们为什么要使用RLD？

RLD最常用于具有重大财务责任的项目中，或者是有多团队合作的项目。尽管RLD是基于一组客观的度量来构建用户体验，但它在大型生产环境中的广泛使用，很大程度上是为了降低风险的结果。

在RLD中，游戏元素的修改和创建是基于对用户数据的观察和数学回归方法创建的近似值。RLD的主要优点是，它通过量化通常被认为是过于无形或抽象而无法用传统方法表示的生产过程，将设计师团队联系起来。

对学生和那些学习设计的来说，RLD还是一个有效的工具。与“禅系”设计不同，禅系的设计更倾向于经验和直觉，而不是具体的度量。而RLD方法提供了一个框架和流程，可以帮助有效减轻设计中的某些奥秘(黑盒)。许多采用RLD方法的设计师最终将其概念融入到自己的设计风格中，并创造出一种Zen/RLD的混合体，这种混合体由经验告知，由逻辑推进。

行业工具&必备知识

RLD受益于这样一个事实：即实现它所需的许多工具都是现成的，有时是免费的，而且通常都有完整的文档记载。尽管一些大型发行商和开发者已经开发了他们自己的内部工具，但是你也可以实现自己的RLD Pipeline。

• 网格纸（是的，我说纸！）

• 尺子，笔，量角器，三角尺，科学计算器等
  

• 某种类型的电子表格应用程序
  

除了工具之外，对数学的良好理解也将大有帮助。

本文的目的&RLD手册的后续更新

本文（和后续文章）旨在为希望将RLD用作其自身设计过程一部分的人员提供参考。本系列涵盖RLD的许多示例，以及它们是如何作为开发和分析工具来实现的。重要的是要注意，本系列文章是游戏设计的广泛知识体系的一部分。在整个系列中，你将看到其他来源的链接和参考。我强烈建议你能花时间阅读这些作者的作品。最重要的是要承认设计过程通常是非常个人化的，你最终需要选择最能引起共鸣的模型和结构。

流程和“不固定”的东西：我们如何创建难度编号？

要了解我们如何在RLD流程中创建难度编号，我们需要了解两个主要问题：

1. 从数学上讲，复杂度的线性增长往往会导致游戏难度的指数级增长。可以认为这是你的RLD表格和玩家实际心理之间的联系，它们与这些表格的最终产品相互作用。

2. RLD始终是起点，并且设计中总会有一些无法用编号客观表达的元素。

3. 当编号失败时，将朝着混乱的方向去创建有趣的游戏关卡体验。

线性增长&指数难度

为了理解我们的RLD编号来自何处，我们需要仔细检查第一点。线性复杂度，会导致难度呈指数级上升。维数是此过程中使用的关键术语之一。从数学上讲，维数是我们枚举一组修饰符(Modifier)的所有可能结果所需的空间维数。

举例来说，假设我们基于六面骰子的结果来创建游戏。这个六面骰子将被视为我们的修饰符。从统计学上讲，我们说六面骰子是一个概率空间，由六个结果组成。玩家可以掷骰子，并有六分之一的机会掷出任何数字。这种类型的“事件”只有一个维度，因为我们只需要一个轴就可以。虽然这有点平淡无奇，但我们的枚举看起来像这样……（图1）

图1

如果我们将游戏扩展到包含两个骰子（修饰符）的结果，那么我们需要使用两个轴来枚举一组事件（图2）。

图2

在两次掷骰子事件中，我们可以看到一个轴是如何修改另一个轴(一加一等于二)，依此类推。我们还可以看到每次一个元素被添加到我们的设计中时，它是如何指数级增加玩家必须处理的潜在的排序结果。通过使用2个六面骰子，我们已经从6个结果变成了36个结果。不仅如此，通过添加一个额外的修饰符，某些结果出现的概率将变得更加复杂，这将会变的有趣起来。通过简单地使用两个修饰符，我们得到了一个更为复杂的概率空间：像总值为2或12的事件，变成了36分之一的概率事件，而总值合计为7的事件则变成了六分之一的概率事件。尽管线性增长的修改导致了概率空间呈指数级上升，人类有能力应对这些巨大的概率空间。许多人认为，这是我们在模式识别中找到这种乐趣的原因之一。

我们可以用不同的方式将这一概念可视化，其中一种方法是通过将玩家在任何一点(阶段)上可能拥有的选项数量作为分支决策树来考虑。在上面的图片中，我们可以看到在任何一个阶段（左）有三个选项比仅只有两个（右）要复杂得多。

注：19.11.12日凌晨时，数值策划群的一位群友所提到的关卡中的层次感便是由此而来，实质上是通过不同阶段所面临的概率空间来进行控制。

图3

图3描绘了RLD问题——每当我们修改或添加一个元素到游戏中时，难度的增长率不是线性的，而是呈现出指数级增长的趋势，直到游戏将变得完全不可能通过的程度。

创建我们的RLD编号

既然我们理解了复杂度的线性增加是如何导致难度指数增加的，那么现在可以将其纳入关卡设计的上下文(环境)中。假设你面临一个跳跃挑战，平台之间的间隙呈线性递增。此示例是使用默认的物理和控件类型在Unreal Development Kit（UDK）中创建的。在这里，我创建了一个测试关卡来了解我的空间度量，即了解实际空间测量值与我作为玩家的经验之间的关系。（图4）

图4

在这里我有四个平台，我想在它们之间跳跃。每个连续的平台都使用的是间隙的线性增加。在此示例中，我每次都将相继的每个平台通过16UU（虚幻单位/现实世界中的测量值大约为32厘米）[1]隔开。使用此空间测试，我将要求一组新的测试人员在没有任何预先培训的情况下在平台之间跳转。每次测试完成后，我都会记录每个平台上的失败次数，当然我也会亲自观察这些测试，这样我就可以将任意数字等同于玩家的经验。这些类型的实验真正有趣的是，你会发现失败率始终会呈指数级增长，即使是在分离平台中的间隙仅呈线性增长的情况下。

难度总是提升到指数增长点。当你试图以图形方式绘制数据时，这是最好的表示方法。基于这个准确的实验，我发现十分之一的测试者在第一次尝试时就没有通过简单跳跃。十分之二的测试者在第一次尝试中没有通过中等跳跃，十分之六的测试者在第一次尝试中没有通过困难跳跃。然后，这导致我创建了一个表格（图5），有三个难度等级：简单、中等和困难。然后，根据测试数据的失败率为每个难度等级分配一个数字。“ RLD难度值”是每十次尝试中的失败尝试次数。最困难的一种跳跃，现在被分配的难度是“六”，因为十次尝试中有六次失败，并且这种模式的延续遍及到我的表格。

图5

需要注意的一件重要的事情是，简单的任务总是需要一些风险因素，并且难度在成为不可能之前是有限度的。（图6）

图6

修饰符&尺寸

所以我们现在有了一组简单的数字，可以用来设计跳跃挑战。但是这些数字做出了一些假设

1.玩家将总是跳至处于相同水平高度的平台上。

2.连续八次轻松跳跃的挑战和一次困难跳跃的挑战一样困难。

从经验中我们知道，事实并非如此。为了纠正这两个问题，我们需要查看我们的修饰符是什么，以及它们的值应该是什么。

图7

在此示例的上下文(环境)中，我们应该考虑的第一个修饰符应该是重力（图7）。我们知道，在玩家将无法到达平台之前，平台的高度是有限的。我们也知道，平台会有一个非常低的位置(Point)，以至于玩家着陆时会因重力而导致死亡。通过进行空间测试，我们可以量化这些数字，并使用一些简单的数学方法从这些点开始向后计算。

图8是使用任何新游戏引擎时应创建的沙箱环境类型的示例。这些环境将根据游戏而变化，但是在第一人称游戏（UDK最适合这种环境）的情况下，你将需要一种方法来测试诸如奔跑速度，跳跃距离等内容。最重要的是，这些类型的测试环境对于了解游戏的“感觉”是非常宝贵的。基于此交互，尝试将感觉转化为一个客观的度量体系。

图8

UDK中创建的一系列跳跃平台-我将使用的引擎。每组由九个不同的平台组成，这些平台逐渐增加高度和间隙的宽度。这个沙箱的目的是寻找出玩家可以做什么的极限，然后将其用作我们的最大跳跃/(不可能跳跃)值，以此计算出我们的RLD度量。

注：这里要提及一下我所在团队的编剧，与他合作制作关卡时，他通过数学方法的方式准确地计算出玩家的极限跳跃距离以及可跳跃高度，与此处所呈具有异曲同工之妙。此种通过计算基于玩家处所得数值驱动设计的方式，为建立一套客观的度量体系打好了基础。

图9

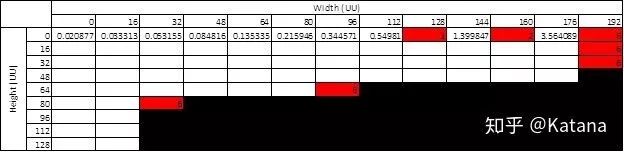
我们从最初的测试数据中知道，对于一个在不同水平高度的平台之间跳跃的玩家来说，我们的RLD编号是什么。我们知道，有十分之一的测试人员未能通过128UU跳跃，十分之二的测试人员未能通过160UU跳跃，十分之六的测试人员未能通过192UU跳跃（在上表中以红色突出显示）。基于此数据，我们现在知道，对于概率空间中宽度x高度的任何单个排列，我们都不应超过RLD编号为六的值。

在这一点上，您需要动手做一些数学运算-特别是我们需要使用我们拥有的数据，并找到最好的方法来插值丢失的数据。我们知道难度往往是指数级的，因此有理由认为我们应该考虑将指数回归作为起点。="http://www.xuru.org/rt/TOC.asp">可以在此处找到一套回归工具。

图10

使用该工具（图10），输入了每个点的数据。有时，你会发现需要尝试多种回归方法，然后才能获得可接受的误差范围。在这种情况下，指数回归不起作用，而对数回归则起作用。（图11）

图11

现在我已经得到了一个公式来使用，然后我可以使用这个公式来插值一个序列中丢失的所有数据。当我将结果图形绘制出时，可以看到我的指数级曲线开始形成。我们现在得到的是沿一个轴的每个排列的近似失败率。现在，我们的任务是回到我们创建的空间测试中，并试图找出每个序列的极限。就本示例而言，我们将使用6这个数字来表示最大值。）

图12 [2]

至此，你有两个选择，我将按照优先顺序列出它们。

1.根据你对问题的理解插入剩余值，但仅使用数字1、2和6表示从容易到困难 //即手动控制

2.使用回归工具以数学方式计算出这些值。

尽管方法二在数学上是正确的，但它往往不能准确地反映出问题的心理影响。例如，当你跑到其中一个壁架上时，可能会出现怀疑、紧张、放松等内部状态，从而扭曲实际结果。正是因为这个原因，我个人喜欢手动插值。同样，这再次证明了RLD是设计中某些元素的一个很好的起点。从上表中可以看到，我发现高度的小幅增加并没有真正使跳跃挑战变得更加困难，直到我们接近64UU高。一旦确定了这些最高点，我们就可以定义任何超出限制的内容（用黑色突出显示）或任何实际上不应视为风险的内容（即值小于1）。

对于类似的情况，你通常会发现你最终得到了一组模仿该模式的RLD编号。（图13）

图13 [3]

你可以通过使用绘图工具在试验系统中对这些曲线中的每条曲线进行微调，也可以使用用于创建原始序列的回归工具。试错法涉及在每个序列上实时绘制数据图形，然后调整每个序列中的数字，直到获得图形化的斜率，类似于使用正确的对数回归方法创建的斜率。

现在，如果你是一名设计师，并且对用于内插这些值的时候所用到的数学计算感到迷惑不解，那么你需要听听我的讲解，让我来帮助你弄清楚这些值的秘密，信不信由你。

汽车售后ECU(电子控制单元)调整软件通常具有表格系统，该表格系统将基于有限的数据集自动执行对数，指数和多项式回归！它们的工作方式通常与Microsoft Excel的线性回归工具相同，但使用的是经过修改的公式。最好的部分是，如果你计划对你的RLD编号进行规范化，将其打入你选择的调谐软件中，它将为你提供相当完整的数据点集，供你进行调整！

任意的修饰符

在此示例的上下文中，我们需要考虑的最后一个修饰符是玩家到达检查点之前所需的连续跳跃量。连续的步数越多，难度就越大-尽管有时很难找到一个客观的来源来帮助我们为这样的修饰符定义一个数字。与重力修正不同的是，在我们认为它是“不可能”的值之前，它可能是一个接近无穷大的数。在这种情况下，你需要使用任意的修饰符。即使这些数字是任意的，你也需要基于某种逻辑。

图14

在图14中，我们有三个不同部分的跳跃挑战。每个区域都被一个“安全区域”分割，玩家可以在这个区域休息并选择进入下一个挑战区域。作为设计师，我们需要一些方法来定义每个部分所采取的步数对难度造成的影响。由于每个安全区域的步数都可能会很长，因此选择一个数字序列（在绘制图形时保持一个相当一致的斜率）非常重要。实际上，可以从音频工程领域获得一个好的经验法则。如果你有一个非常安静的小提琴演奏者，你需要多少个额外的小提琴演奏者将音量加倍？这听起来很奇怪，你大约需要十个小提琴演奏者才能使音量加倍！同样的原理也适用于这个例子和对困难的感知。因此，你的数字序列应该是一个接近线性的发展(near linear progression)。

图15

在上面的例子中，我创建了一系列的修饰符，然后我将可以使用它们来修改跳跃挑战中每个部分的整体难度。这些数字是以上面的小提琴例子为基础的–当我们将某物乘以10时；我们大概将感知到的难度翻了一番。作为首席设计师，你将始终需要为这样的系统指定一个上限，以便团队中的其他人可以共享一套一致的游戏空间开发规则。

数字心理学

有人认为RLD是一种过度解构主义、数学化和枯燥的游戏体验设计方式。当单独使用时，似乎没有任何类型的测试。这似乎是事实，但是当正确和一致地使用时，RLD在塑造用户体验方面则是一个强大的工具。困难在游戏体验中扮演着重要的角色，为了保持玩家的参与度，游戏的设计应始终带有焦虑的高峰和低谷，但是在这种“自然”的过程中意想不到的中断则会是非常有害的。（图16）

图16 [4]

RLD的制作经验

既然我们对修饰符的影响有了清晰的认识，那么我们就可以着眼于制作关卡中的元素-特别是跳跃挑战。尽管RLD看起来像是简陋和没有价值的，但是有一个非常可衡量的心理因素可以使它正确（和错误！）。理想的游戏体验是，焦虑会随着时间的流逝而增加，并且在设计中的元素没有去破坏心流或者沉浸感。而难度对于这种沉浸感和心流具有最大的影响。当事情太容易时，我们往往会感到无聊，而当事情太难时，我们就会感到沮丧。通过使用RLD来打造我们的游戏体验，我们确保难度遵循这个久经考验的真实公式。

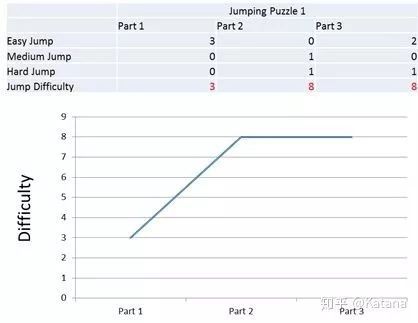
为了展示游戏体验和通过RLD进行细致的关卡构建之间的联系，让我们继续跳跃挑战的示例。我们想设计一个有三个截然不同的部分的跳跃挑战（图17）。每个部分都有一个安全区域作为检查点。我们已经定义了每个跳跃类型的RLD编号，首先基于用户测试，然后通过数学回归（以及更多测试）。我们还通过包含的另外两个修饰符扩展了挑战的维度：重力和步数。现在是时候拿出图表画出一个概念了。

图17

如果要在不带修饰符的情况下绘制此示例的图，那么我们将得出类似于以下示例的内容（图18）。我们面临的挑战很容易开始，但难度却大大增加。

图18

通过只绘制一个修饰符，我们的图形表明我们已经创造了一个突破性的挑战。将焦虑/无聊标签应用到该图时，你可以看到我们如何走出流动通道并进入危险区域（图19）。但是，我们错过了这一跳跃挑战的两个重要修饰符。

图19

一旦添加了额外的修饰符，我们的图表就开始更能反映玩家对挑战的感知（图20）。我们在挑战的第二部分看到的极端峰值有所缓解。但是，挑战的第二部分仍然存在问题。

图20

RLD总是一个修改和完善的过程。关于这一挑战最明显的事情是，中间区域在目前的形式下太困难了。我们需要回头看看修饰符，看看我们能做什么来解决这个问题。我们有几个选择，可以根据我们的指标使用；

1.缩小间隙

2.保持间隙不变并调整垂直度

3.减少步数

RLD的最重要元素之一是识别度量系统的优先级。你将需要至少三个指标–主一级、二级和三级。指标之间的关系通常总是可传递的。也就是说，调整一级指标将产生最大的影响，并且将对二级和三级指标等产生级联效应。

在这个挑战中，如果我只是简单地使用较小的跳跃（即简单的跳跃），那么我知道这很可能会改变挑战，从太难变成太容易。然后我遵从我的第二个指标-垂直修正/重力修正。根据逻辑，要求玩家跳到较低的平台会稍微容易一些。我们仍然保持相同的间距，但只需应用其中一个修饰符来调整数字。

注：指标这个词语等同于度量

基于此逻辑，你可以使用之前创建的表来创建跳跃的组合，从而略微降低难度。在这种跳跃式挑战的情况下，只需将每个连续的步调降低16UU，即可得到理想的结果（图20）。重要的是要注意，我在绘制图纸之前参考了表格并计算了实际示例。这是在预生产过程中进行RLD工作的好处–迭代变得更快，解决设计问题变得更加面向流程，而不是随意的用户需求评价过程。

图21

当我们绘制最终结果的图表时，我们得出了一个大大改进的难度分布（图21）。请记住，困难永远是相对的-随着玩家技能的提高，人们对什么是（不什么是）困难的理解也会随之增加。尽管此图显示了跳跃挑战进入焦虑区域的第三部分，但这应该是你的分布大致所在的位置。

混乱与RLD的主要度量

混乱是当你从这个跳跃挑战开始时，玩家对难度的感知发生的变化…（图22）

图22

对此……（图23）

图23

在这两种情况下，我们的跳台都使用相同的高度和距离度量进行分布，但是挑战的表现形式是不同的，甚至可能是混乱的。

现在当我说混乱时，我的意思不是指杂乱无章或无序，随机和无知的设计决策。在RLD的上下文中，混乱是指所有不能轻易以量化和客观的方式来表达的修饰符（无论是游戏还是玩家的思维，在游戏体验中都是显而易见的）。尽管我们没有量化这些现象，但是我们还是在RLD的过程中使用它们并加以考虑。换句话来说，混乱是RLD的一部分，我们不能用数字来表示它，但它仍然是玩家体验的组成部分。

混乱元素的一个很好的例子是，考虑到美学在跳跃挑战中对难度的感知所起的作用。我们可以在美学上以多种方式实现相同的跳跃挑战。虽然我们可能会改变如何使用各种艺术手段来实现难题或挑战，但数值难度和感知难度可能会有很大的不同。例如，难题或挑战的一种实现可能会有震耳欲聋或者是无声音频，它们使玩家不知所措，而另一种版本则可能是相同的形式，通过音频以外的艺术手段表现出来。

那么哪一个更困难呢？

答案是，从RLD的角度来看，两者都同样困难。只不过单纯从美学(每个人不同的审美观点)上来看，其中一个相对于另外一个会更难一些。

在我的下一篇文章中，我将探讨全局度量的概念，以及我们如何解释这些影响难度度量的“其他”元素。

注：

[1] The conversion between UU and real world measurements depends largely on how the underlying physics system has been written. Although many different games use Unreal Engine, the translation of UU to real world measurements varies slightly.

[2] The black sections indicate permutations that are off limits. In the case of Figure 12, this blacked out sections are impossible under normal circumstances

[3] Just like the example given in Figure 12, more sections have been blacked out in this table to represent permutations which are too simple to be considered a puzzle.

[4] This explanation of the “Flow Channel” is derived from Jesse Schell. The art of game design a book of lenses. Elsevier/Morgan Kaufmann, 1st edition, August 2008.

相关阅读：

如何在游戏设计中引导玩家？剖析2D射击游戏设计中的压缩和漏斗理论

原文链接

https://link.zhihu.com/?target=https%3A//www.gamasutra.com/blogs/LukeMcMillan/20130806/197147/The_Rational_Design_Handbook_An_Intro_to_RLD.php

译者专栏：

https://zhuanlan.zhihu.com/p/91338673

• 稿件合作：一元（微信：smallkisshe）

• 商务合作：Amber（微信：lcxk6876767）

• 投稿邮箱：[email protected]