前言
在上一篇中,我们已经介绍了如何在DEAP中实现进化算法的基本操作,在这一篇中我们试图将各个操作组装起来,用进化算法解决一个简单的一元函数寻优问题。
进化算法实例 - 一元函数寻优
问题描述与分析
给定一个函数,求解该函数的最大值。
该函数图像如下:
该函数的最大值应该出现在处,值为。
可以看到该函数有很多局部极值作为干扰项,如果进化算法过早收敛,很容易陷入某个局部最优。
问题的编码与解码
对于该问题,可以选取很多不同的编码方式。本文计划采用二进制编码,精度要求到6位,那么首先应当确定编码的长度与解码方式。由于有:
所以我们需要的二进制编码长度为26。
利用DEAP自带算法求解
DEAP自带的进化算法介绍
DEAP自带的算法都比较基础,通常可以用来测试问题描述、编码方式和交叉突变操作组合的有效性。需要比较复杂的进化算法时,可以通过在已经有的算子上进行扩充。
| 算法 | 描述 |
|---|---|
| eaSimple | 简单进化算法 |
| eaMuPlusLambda | 进化算法 |
| eaMuCommaLambda | 进化算法 |
简单进化算法 :deap.algorithms.eaSimple
DEAP中预置的简单进化算法流程描述如下:
- 根据工具箱中注册的
toolbox.evaluate评价族群 - 根据工具箱中注册的
toolbox.select选择与父代相同个数的育种个体 - 在族群中进行第一次循环,用工具箱中注册的
toolbox.mate进行配种,并用生成的两个子代替换对应父代 - 在族群中进行第二次循环,用工具箱中注册的
toolbox.mutate进行变异,用变异后的子代替换对应父代 - 从1开始重复循环,直到达到设定的迭代次数
需要注意的是在这个过程中,生成子代有四种情况:受到配种影响;受到变异影响;既受到配种也受到变异影响;既不受配种影响也不受变异影响。
对应的伪代码可以表述为:
evaluate(population)
for g in range(ngen):
population = select(population, len(population))
offspring = varAnd(population, toolbox, cxpb, mutpb)
evaluate(offspring)
population = offspring
进化算法:deap.algorithms.eaMuPlusLambda
该算法的流程如下:
- 根据工具箱中注册的
toolbox.evaluate评价族群 - 在族群中进行循环,在每次循环中,随机选择crossover,mutation和reproduction三者之一:如果选择到crossover,那么随机选择2个个体,用工具箱中注册的
toolbox.mate进行配种,将生成的第一个子代加入到后代列表中,第二个子代丢弃;如果选择到mutation,用工具箱中注册的toolbox.mutate进行变异,将变异后的子代加入到后代列表中;如果选择到reproduction,随机选择一个个体,将其复制加入到后代列表中 - 根据工具箱中注册的
toolbox.select,在父代+子代中选择给定数量的个体作为子代 - 从1开始重复循环,直到达到设定的迭代次数
注意在这个子代生成的过程中,子代不会同时受到变异和配种影响。
对应的伪代码可以表述为:
evaluate(population)
for g in range(ngen):
offspring = varOr(population, toolbox, lambda_, cxpb, mutpb)
evaluate(offspring)
population = select(population + offspring, mu)
进化算法:deap.algorithms.eaMuCommaLambda
与基本相同,唯一的区别在于生成子代族群时,只在产生的子代中选择,而丢弃所有父代。
对应的伪代码可以表述为:
evaluate(population)
for g in range(ngen):
offspring = varOr(population, toolbox, lambda_, cxpb, mutpb)
evaluate(offspring)
population = select(offspring, mu)
调用DEAP自带的进化算法
在调用DEAP自带的算法时需要注意的是,由于内置算法调用的alias已经提前给定,因此我们在register的时候,需要按照给定名称注册。
例如toolbox.register('crossover', tools.cxUniform)就不能被内置算法识别,而应当按照要求,命名为mate,并且显示给出交叉概率: toolbox.register('mate', tools.cxUniform, indpb = 0.5)
按照要求,使用预置的算法需要注册的工具有:
toolbox.evaluate:评价函数
toolbox.select:育种选择
toolbox.mate:交叉操作
toolbox.mutate:突变操作
代码与测试
from deap import algorithms
random.seed(42) #确保可以复现结果
# 描述问题
creator.create('FitnessMax', base.Fitness, weights=(1.0,)) # 单目标,最大值问题
creator.create('Individual', list, fitness = creator.FitnessMax) # 编码继承list类
# 个体编码
GENE_LENGTH = 26 # 需要26位编码
toolbox = base.Toolbox()
toolbox.register('binary', bernoulli.rvs, 0.5) #注册一个Binary的alias,指向scipy.stats中的bernoulli.rvs,概率为0.5
toolbox.register('individual', tools.initRepeat, creator.Individual, toolbox.binary, n = GENE_LENGTH) #用tools.initRepeat生成长度为GENE_LENGTH的Individual
# 评价函数
def decode(individual):
num = int(''.join([str(_) for _ in individual]), 2) # 解码到10进制
x = -30 + num * 60 / (2**26 - 1) # 映射回-30,30区间
return x
def eval(individual):
x = decode(individual)
return ((np.square(x) + x) * np.cos(2*x) + np.square(x) + x),
# 生成初始族群
N_POP = 100 # 族群中的个体数量
toolbox.register('population', tools.initRepeat, list, toolbox.individual)
pop = toolbox.population(n = N_POP)
# 在工具箱中注册遗传算法需要的工具
toolbox.register('evaluate', eval)
toolbox.register('select', tools.selTournament, tournsize = 2) # 注册Tournsize为2的锦标赛选择
toolbox.register('mate', tools.cxUniform, indpb = 0.5) # 注意这里的indpb需要显示给出
toolbox.register('mutate', tools.mutFlipBit, indpb = 0.5)
# 注册计算过程中需要记录的数据
stats = tools.Statistics(key=lambda ind: ind.fitness.values)
stats.register("avg", np.mean)
stats.register("std", np.std)
stats.register("min", np.min)
stats.register("max", np.max)
# 调用DEAP内置的算法
resultPop, logbook = algorithms.eaSimple(pop, toolbox, cxpb=0.5, mutpb=0.2, ngen=50, stats = stats, verbose = False)
# 输出计算过程
logbook.header = 'gen', 'nevals',"avg", "std", 'min', "max"
print(logbook)
计算过程输出(在保存的结果中,nevals代表该迭代中调用evaluate函数的次数;另外也可以令verbose=True直接在迭代中输出计算过程):
gen nevals avg std min max
0 100 279.703 373.129 -0.406848 1655.79
1 53 458.499 416.789 0.154799 1655.79
2 59 482.595 461.698 0.00177335 1655.79
3 52 540.527 472.762 -0.0472813 1655.79
4 59 580.49 514.773 0.0557206 1655.79
5 62 693.469 576.465 -0.393899 1655.79
6 71 875.931 609.527 0.000831826 1656.52
7 62 946.418 608.838 0.221249 1656.52
8 67 881.358 636.562 0.06291 1657.42
9 55 937.741 636.038 0.231018 1657.42
10 59 942.68 662.51 0.00094194 1657.42
11 50 990.668 641.284 1.36174 1657.42
12 49 1056.75 661.558 -0.392898 1657.42
13 60 1254.48 596.379 -0.374487 1657.42
14 56 1196.38 667.938 0.0073118 1657.42
15 61 1255.25 655.171 0.0130561 1657.42
16 57 1258.77 639.582 0.20504 1657.42
17 72 1328.39 587.822 11.0895 1657.42
18 66 1331.57 610.036 0.298211 1657.42
19 67 1297.66 632.126 -0.231748 1657.42
20 64 1246.8 610.818 0.0335697 1657.42
21 58 1099.19 690.046 0.0503046 1657.42
22 60 1068.91 664.985 0.0591922 1657.42
23 49 1243.47 612.2 0.00160086 1657.42
24 47 1231.47 658.94 -0.202828 1657.42
25 57 1233.48 657.109 0.0262275 1657.42
26 53 1410.59 534.754 0.877048 1657.42
27 71 1162.42 704.536 -0.257036 1657.42
28 52 1259.11 639.283 7.61025 1657.42
29 61 1312.6 615.661 1.40555 1657.42
30 56 1251.42 651.842 -0.0276344 1657.42
31 68 1200.02 678.454 0.00783006 1657.42
32 58 1198.2 675.925 -0.0726268 1657.42
33 61 1196.74 679.65 -0.135946 1657.42
34 60 1236.89 635.381 0.0133596 1657.42
35 50 1328.18 600.071 3.61031 1657.42
36 40 1357.62 599.045 -0.367127 1657.42
37 51 1299.96 633.932 -0.0674078 1657.42
38 48 1324.36 610.043 0.95255 1657.42
39 55 1323.23 566.232 0.987755 1657.42
40 58 1282.45 640.85 0.1648 1657.42
41 54 1335.26 593.431 -0.317349 1657.42
42 53 1330.78 593.921 0.0287983 1657.42
43 60 1332.02 597.941 1.32028 1657.42
44 65 1239.09 645.678 0.00144193 1657.42
45 71 1287.96 625.504 -0.372238 1657.42
46 51 1397.84 520.398 0.0150745 1657.42
47 66 1311.83 591.556 0.258935 1657.42
48 66 1160.49 694.509 0.163166 1657.42
49 50 1271.95 642.396 0.000437735 1657.42
50 61 1288.53 619.33 0.149628 1657.42
查看结果:
# 输出最优解
index = np.argmax([ind.fitness for ind in resultPop])
x = decode(resultPop[index]) # 解码
print('当前最优解:'+ str(x) + '\t对应的函数值为:' + str(resultPop[index].fitness))
结果:
当前最优解:28.308083985866368 对应的函数值为:(1657.4220524080563,)
可以看到遗传算法成功避开了局部最优,给出的结果非常接近全局最优解28.309了。
自行编写算法求解
代码与测试
自行编写通常来说会需要比内置函数更长的篇幅,但是也能获得更大的自由度。下面是一个用锦标赛交叉、位翻转突变求解同样问题的例子:
import random
from deap import creator, base, tools
from scipy.stats import bernoulli
random.seed(42) # 确保结果可以复现
# 描述问题
creator.create('FitnessMax', base.Fitness, weights=(1.0,)) # 单目标,最大值问题
creator.create('Individual', list, fitness = creator.FitnessMax) # 编码继承list类
# 二进制个体编码
GENE_LENGTH = 26 # 需要26位编码
toolbox = base.Toolbox()
toolbox.register('binary', bernoulli.rvs, 0.5) #注册一个Binary的alias,指向scipy.stats中的bernoulli.rvs,概率为0.5
toolbox.register('individual', tools.initRepeat, creator.Individual, toolbox.binary, n = GENE_LENGTH) #用tools.initRepeat生成长度为GENE_LENGTH的Individual
# 评价函数
def eval(individual):
num = int(''.join([str(_) for _ in individual]), 2) # 解码到10进制
x = -30 + num * 60 / (2**26 - 1) # 映射回-30,30区间
return ((np.square(x) + x) * np.cos(2*x) + np.square(x) + x),
toolbox.register('evaluate', eval)
# 生成初始族群
N_POP = 100 # 族群中的个体数量
toolbox.register('population', tools.initRepeat, list, toolbox.individual)
pop = toolbox.population(n = N_POP)
# 评价初始族群
fitnesses = map(toolbox.evaluate, pop)
for ind, fit in zip(pop, fitnesses):
ind.fitness.values = fit
# 进化迭代
N_GEN = 50 # 迭代代数
CXPB = 0.5 # 交叉概率
MUTPB = 0.2 # 突变概率
# 注册进化过程需要的工具:配种选择、交叉、突变
toolbox.register('tourSel', tools.selTournament, tournsize = 2) # 注册Tournsize为2的锦标赛选择
toolbox.register('crossover', tools.cxUniform)
toolbox.register('mutate', tools.mutFlipBit)
# 用数据记录算法迭代过程
stats = tools.Statistics(key=lambda ind: ind.fitness.values)
stats.register("avg", np.mean)
stats.register("std", np.std)
stats.register("min", np.min)
stats.register("max", np.max)
logbook = tools.Logbook()
for gen in range(N_GEN):
# 配种选择
selectedTour = toolbox.tourSel(pop, N_POP) # 选择N_POP个体
selectedInd = list(map(toolbox.clone, selectedTour)) # 复制个体,供交叉变异用
# 对选出的育种族群两两进行交叉,对于被改变个体,删除其适应度值
for child1, child2 in zip(selectedInd[::2], selectedInd[1::2]):
if random.random() < CXPB:
toolbox.crossover(child1, child2, 0.5)
del child1.fitness.values
del child2.fitness.values
# 对选出的育种族群进行变异,对于被改变个体,删除适应度值
for mutant in selectedInd:
if random.random() < MUTPB:
toolbox.mutate(mutant, 0.5)
del mutant.fitness.values
# 对于被改变的个体,重新评价其适应度
invalid_ind = [ind for ind in selectedInd if not ind.fitness.valid]
fitnesses = map(toolbox.evaluate, invalid_ind)
for ind, fit in zip(invalid_ind, fitnesses):
ind.fitness.values = fit
# 完全重插入
pop[:] = selectedInd
# 记录数据
record = stats.compile(pop)
logbook.record(gen=gen, **record)
# 输出计算过程
logbook.header = 'gen',"avg", "std", 'min', "max"
print(logbook)
计算过程输出:
gen avg std min max
0 453.042 403.079 0.0541052 1533.87
1 494.408 419.628 0.860502 1626.41
2 543.773 465.404 -0.11475 1626.41
3 551.903 496.022 -0.0620545 1626.41
4 590.134 538.303 -0.0423912 1626.41
5 552.925 523.084 -0.348284 1544.09
6 580.065 532.083 0.000270764 1544.09
7 610.387 567.527 0.0294394 1574.38
8 667.447 556.671 -0.16236 1525.22
9 722.472 551.263 -0.39705 1524.89
10 698.512 548.705 0.0240564 1542.15
11 748.871 585.757 -0.405741 1542.15
12 717.023 580.996 0.00352434 1542.15
13 701.257 575.739 0.0797344 1542.15
14 720.325 593.033 -0.322945 1542.15
15 705.138 612.55 0.846468 1627.42
16 725.673 616.072 0.0259165 1641.05
17 683.245 609.737 -0.0759172 1630.68
18 613.711 613.64 -0.0448713 1627.25
19 648.058 579.645 -0.319345 1648.62
20 655.742 570.835 -0.247798 1613.19
21 692.022 541.547 -0.160214 1543.01
22 737.027 557.312 0.175429 1543.01
23 825.825 595.845 -0.403073 1542.95
24 831.611 600.052 -0.397646 1645.6
25 991.433 564.623 0.095375 1641.16
26 842.529 641.466 -0.406455 1641.16
27 906.907 622.024 4.64596 1641.16
28 791.317 633.509 -0.234101 1641.16
29 896.355 598.829 0.339045 1641.16
30 781.726 625.868 0.0195279 1647.45
31 774.75 645.621 0.134108 1647.45
32 789.524 631.395 -0.388413 1647.45
33 985.497 631.871 0.00160795 1654.93
34 990.838 662.935 0.00156172 1657.21
35 1013.72 695.145 -0.266597 1652.41
36 1073.47 697.062 -0.0762617 1652.32
37 1118.98 667.797 0.508095 1652.32
38 1219.86 602.05 -0.256761 1652.39
39 1247.71 628.152 0.00243654 1652.39
40 1290.97 613.243 -0.374519 1652.39
41 1298.95 607.829 0.0630793 1652.41
42 1309.81 599.807 0.0235305 1652.47
43 1214.13 658.237 0.0027164 1653.03
44 1244.05 656.009 -0.329403 1653.13
45 1369.44 543.688 0.000339235 1653.05
46 1283.87 602.252 0.204417 1653.19
47 1157.28 686.628 0.00359533 1653.19
48 1284.39 630.622 0.0769602 1653.19
49 1301.76 608.879 0.0775233 1656.45
查看结果:
# 输出最优解
index = np.argmax([ind.fitness for ind in pop])
x = decode(resultPop[index]) # 解码
print('当前最优解:'+ str(x) + '\t对应的函数值为:' + str(pop[index].fitness))
结果输出:
当前最优解:28.39357492914162 对应的函数值为:(1656.4466617035953,)
结果可视化
# 结果可视化
import matplotlib.pyplot as plt
gen = logbook.select('gen') # 用select方法从logbook中提取迭代次数
fit_maxs = logbook.select('max')
fit_average = logbook.select('avg')
fig = plt.figure()
ax = fig.add_subplot(111)
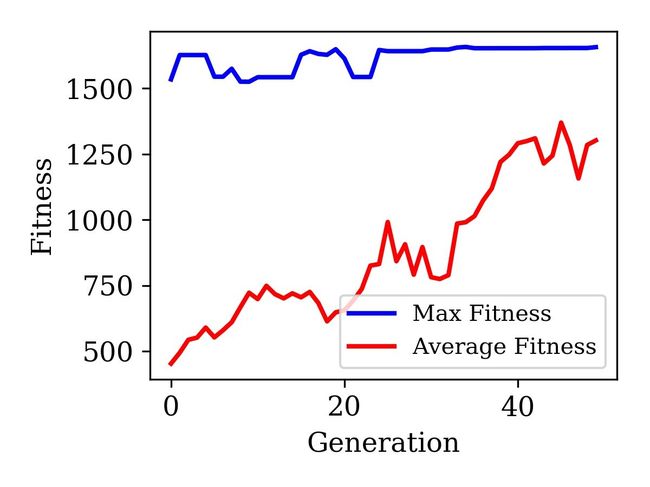
ax.plot(gen, fit_maxs, 'b-', linewidth = 2.0, label='Max Fitness')
ax.plot(gen, fit_average, 'r-', linewidth = 2.0, label='Average Fitness')
ax.legend(loc='best')
ax.set_xlabel('Generation')
ax.set_ylabel('Fitness')
fig.tight_layout()
fig.savefig('Generation_Fitness.png')
得到结果: