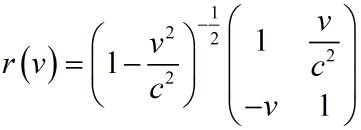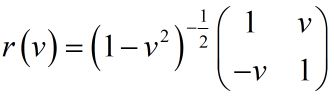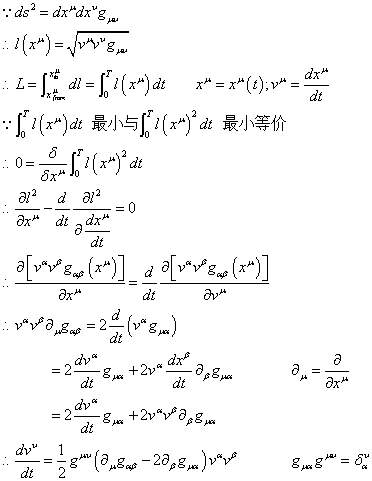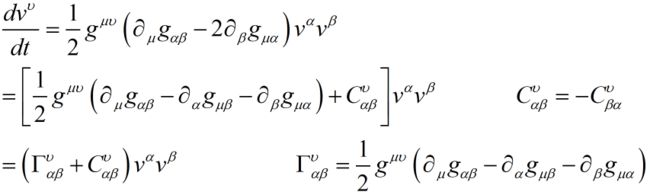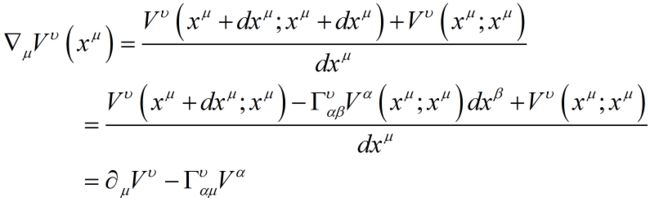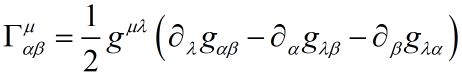这个话题显然不是两三千字可以说玩的,所以我只能写成连续剧啦,哎……
一般我们在教科书上,看到广义相对论的由来基本都是这个样子的:
狭义相对论横空出世,成功地解释了Maxwell方程和迈克尔-莫雷实验等一些列别的当年有问题的实验,接着人们以电磁理论的狭义相对论化的成功案例为出发点,开始尝试当年已有的各种别的理论的相对论化,大部分都取得了成功,但在搞牛顿引力的时候发生了不可调和的障碍,等等等等,于是进程中断,最后爱因斯坦通过水桶实验进而想到了等效原理,从引力质量与惯性质量的相等发现了引力与非匀速直线运动的等价,并最终发现了广义相对论,最终解决了这个大难题。当然在这个序列中肯定还会提一下牛顿引力在当时看来的一些问题比如水星近日点进动,这标志着牛顿引力存在缺陷甚至是根本性的纰漏,所以需要“升级”。
这是最一般的历史流程,我们从狭义相对论出发,自然地将各种线索串联起来,并最终得到了广义相对论。
但,我们也可以从一些完全不同的角度出发来考虑广义相对论的由来,比如,我们接着上次的文章,接着往下走。
在《狭义相对论》一文中,我们已经论述了,在满足一些看上去非常基本没有任何特别之处的条件后,我们自然而然地就得到了狭义相对论所要求的闵科夫斯基时空。
接着,如果我们为时空加上“各向同性”与“时空平移不变”,我们就自然得到了狭义相对论。
那么,一个很自然的问题就来了:如果后面两个条件不加上,会怎么样?
让我们将上面这两个条件换成一个更加宽泛的条件:时空上每个时空点周围的邻域,都同构于一个同样维度的闵科夫斯基时空。
也可以这么说,每个时空点的领域和一个标准的狭义相对论的闵科夫斯基时空之间,只差一个坐标变换。
很显然,这样定义的时空比狭义相对论中的时空要宽泛得多,所以这样的时空及其上的物理学,我们就称为“广义相对论”。
好了,上面是一个框架性的定义,下面开始看看在这个定义下,具体会有一些什么样的好玩的东西。
首先,我们要找出刻画着两者的基础物理量或者说数学对象。
在狭义相对论中,我们已经知道,物质的运动所导致的就是世界线的倾斜,这个过程可以看作是一个时空上的赝转动,或者说Boost,推动。
其中的坐标变换可以写为(为了简化,我们只考虑一个空间方向):
进一步,为了简单又不是一般性,我们可以通过恰当的坐标单位选择,使得这个闵科夫斯基时空的特征速度或者说极限速度为1(这就是自然单位制),从而可以化简为:
这样的坐标变换下,我们最感兴趣的自然就是这么一个东西:里面有什么是不变量么?
容易发现,时空的“长度”是一个不变量:
即,无论v取什么值,这个长度在上述坐标变换下都是不变的。
进一步,这个如果写成真正的三维空间加一维时间的(3+1)维时空形式,那么这个长度就是:
或者可以用张量的手法写为:
而,所有的坐标变换都可以看作是左边的形式不变,改变的是右边的那个张量。同时我们又知道坐标变换对应的就是每个时空点邻域上的那个特有的性质,因此也就是说,这右边的张量现在应该就是我们要找的那个物理量,那个数学对象。
我们称这个张量为“度规张量”,因为它给出了时空上一个邻域内的“长度”的定义。
同时我们也知道,在闵科夫斯基时空中,匀速直线运动所带来的坐标变换是不会改变这个张量的。也就是说,引起度规张量改变的,绝对不是匀速直线运动这么平庸的东西。
因此,我们现在手上所有的就是这么一个东西:
一个时空M,其上的每个点都可以由一组坐标xμ给出,同时,每个坐标位置xμ的邻域内,都有一个只属于其内部的度规张量gμυ(xμ)。
于是,一个很自然的问题就是:在这么一个直观上很“拧巴”的时空上,一个“不受任何外力”的点粒子,会如何运动?
既然说是“不受任何外力”,那也就是说,这枚点粒子的运动是“匀速直线”运动——只不过,现在在这个“拧巴”的时空里,这种“匀速直线”在每一个邻域上都成立,但链接成一个整体的时候则未必了。
这种局部上是匀速直线而整体上却不是的特性,我们可以用一个数学对象来刻画,它成为“联络”。
而,在继续介绍联络之前,我们从另一个角度出发来考虑这个问题。
在传统的物理世界中,“不受外力作用”的粒子的运动轨迹,可以用另一个数学概念来刻画,那就是“最短路径”。
比如在一个什么都没有的空间中,点粒子的运动是直线,因为直线是链接两点的最短路径。而,如果我们来看一个光线从空气射入水中的运动轨迹,此时我们都知道会发生折射现象,而这种折射也可以用“最短路径”来刻画——当然,这里更直观的说法是“最短耗时”。
因此,如果我们将这个原理“借用”到现在的新的时空中,那么这个问题就变成了求这么一个“拧巴”的时空上的最短路径,或者这里更应该说是“极值路径”的问题了:
其中,对线元l的积分和对线元l的平方的积分,在线元l必然不小于零的情况下,很容易证明是等价的,而这里之所以用线元的平方,仅仅是因为这样计算方便(俗称偷懒)。
而,现在的积分其实就是在给定路径x μ(t)的情况下,对这个路径上每一点的线元求积分,即是路径的泛函。而在给定初态末态的情况下,求泛函的极值所对应的路径,要用的就是(固定初末态的)变分为零这个数学工具了,因此后面就是一阵没啥技术含量的计算。
唯一需要说明的,就是度规张量g μυ是存在“逆”的,也就是最后一行右侧的那一段补充:g μυ。这个逆元的作用,就是和度规张量无论以哪种方式惩在一起,最后都得到一个“单位矩阵”,这也是最后一行中比较麻烦的步骤所在。
而,进一步,对于最后一行的结果,我们可以进一步构造如下的东东:
由于现在度规和路径的选择无关,所以这里最后的结果可以说是最一般化以后的结果了,其中Γ部分可以被完全确定下来,而C部分则只能确定到它对于两个下标是反对称的(第二行右侧)。
我们将Γ部分称为时空的“联络”,而C部分称为时空的“扰率”。
其中,在低速情况下,速度矢量v μ的时间分量v t基本保持为1,而其三个空间分量基本为0,从而上面的式子告诉我们:现在点粒子运动受到的“加速度”基本完全就是由度规所决定的了。这就可以类比到各种形形色色的“势能场”上去了,比如我们的终极目标:引力场。
同时,看,我们又看到“联络”这东西了。
联络这货的本意,指的是将一个点的领域和它“隔壁邻居”那个点的领域联系起来的数学对象,即:
你看,这里无穷小间隔的邻域之间坐标变换就是最后那括号中的东西。
因此,回到那个“不受外力作用”的点粒子的“自由”运动问题上来,显然此时既然点粒子的运动不受别的因素的作用,那唯一影响其轨迹的就只是不同点之间的“坐标变换”了,也就是说,只有这个代表了“无穷小间隔上的坐标变换”的联络,是改变点粒子运动轨迹的唯一元凶了——这个结论和上面通过极值曲线得到的结论是温和的。
但,联络这货本身的任意性非常大,而且本身和度规张量没啥关系。
因此,为了消除那些不合适的、非必须的联络的任意性,我们就需要引入一些特殊的限制条件。
让我们考虑这么一个情况:一个点的邻域和闵科夫斯基时空差一个恒等坐标变换,这当然是允许的;而后,它“隔壁”的一个邻点的邻域和这个点的邻域这两者之间差一个空间转动,这当然也是允许的。将这样的构造推广出去,时空的每个点和那个最初的点之间就差一个纯粹的空间转动,别的什么都不差——而且,更重要的是,转动是不会改变度量的。
也就是说,这样得到的时空,从度量的角度来看,和闵科夫斯基时空是完全一直的,但从联络的角度来看,缺暗藏了极大的“引力相互作用”。这样的情况当然是不允许的。
因此,我们就有必要引入一个条件:度规张量在联络作用下是不变的。或者简称呼为“保度规”。
这里就需要解释一下什么叫“不变”了。
让我们考虑标量场在现在这个“拧巴”时空上的“梯度”:
但这个很和谐的关系到了矢量场的“梯度”时,就有点麻烦了,因为现在两个不同时空点上的矢量场隶属于两个不同的邻域,实在两个不同的“闵氏时空”中的。
为了解决这个问题,我们就需要使用联络——它将两个邻域的闵氏时空通过一个坐标变换联系在了一起。
从而,现在对于矢量我们就有:
其中括号中分号后的部分只是为了区分现在这个矢量“隶属于”那个邻域。
现在这个微分法则称为“协变微分”。
然后,由于两个矢量可以和度规张量“合并”称为一个标量,就如一开始说长度线元的时候那样,那么根据微分的莱布尼兹法则,我们就可以很容易地得到关于度规的“协变微分”:
现在,我们终于可以来说说什么叫“度规张量不变”了,这个意思其实就是说对于度规张量的协变微分,在时空上恒等与零:
这个约束条件就被称呼 联络与度规的适配条件,由此我们就可以去掉联络的各种多余的任意性,将其唯一确定为:
你看,和前面通过极值曲线得到的结果是一样的。
非但从两个不同的角度得到的联络是一样的(废话),我们还可以进一步来考虑现在“不受外力作用”的点粒子的运动方程,直接从联络的“坐标变换”的意义出发:既然不受外力作用,那就是说粒子轨迹上的任意一点的切矢量,沿着轨迹的方向看都是“不变”的,即使切矢量在自己方向上的协变微分为零。
用数学公式来写就是:
看上去是不是特简单?而且结果就是上面极值曲线的运动方程。
因此,到这里我们终于可以说:极值曲线和自平行曲线在现在我们的时空中是完全等价的。
当然,在上述推导中,我们是假定了联络对它的两个下标是对称的。我们可以放弃这个要求,从而就可以得到一个反对称的张量C,它是非常任意的,而且,就是在极值曲线的研究中所出现的那个“C部分”。
现在,让我们回顾一下。
在上一篇文章的基础上,我们放弃了“各向同性”与“时空平移不变”这两个要求,该为每个点的邻域都与闵氏时空相差一个坐标变换。这个要求的改变,为我们带来了一个每个点的邻域都不同的时空,且在每个点的邻域这个无穷小局部里,时空观是狭义相对论的,只不过一旦考虑连起来的整体,就不是狭义相对论的了,而是一个处处拧巴的“弯曲时空”。
在这个时空中,我们假定粒子的运动轨迹是极值曲线,然后得到了运动方程与联络的表达。同时,我们又研究了作为连接无穷小间隔的两点及其邻域的坐标变换的联络,并为了消除这种定义的联络的任意性而引入了适配条件,从而得到了粒子的运动方程和联络的表达。
并且,我们发现,这两条路得到的结果,是一样的。
因此,我们现在其实建立在这么三条假设上:
- 假定时空每个点的邻域和闵氏时空就差一个坐标变换;
- 假定粒子运动轨迹是极值曲线(极长或者极短或者驻值)或者自平行曲线;
- 假定度规和联络满足适配条件的约束。
在这三条假定下,我们得到了粒子的运动方程(从极值曲线和自平行入手的结果等价)、联络与度规的关系,以及,相当任意的扰率。
而,爱因斯坦的广义相对论,就是要求扰率恒为零的上述时空的物理理论。
假设我们将扰率恒为零这个假设去掉,我们就得到了爱因斯坦-嘉当理论,其中通过分析我们发现,物质的质量引起时空度规和联络的改变,而物质的自旋则会引起时空扰率的改变。这样的理论在宏观上依然是爱因斯坦的相对论,因为宏观上自旋可以认为可以忽略。但在微观上,特别在致密星体内部,此时自旋就不可忽略,从而可以得到和传统相对论不同的结果。
我们还可以进一步丢掉一些假设。
比如,我们可以去掉度规和联络的适配约束,此时联络是一个自由量,度规是和联络无关的另一个自由量,这样得到的理论在经典范畴里意义不大,但在量子化以后却可以有很不错的表现,被很多前辈用来构造规范场论化的引力理论,然后再将适配约束作为规范条件引入,总之很有意思。
作为比较,传统的广义相对论的量子化方案会考虑将联络作为与身为广义坐标的度规对应的广义动量。
当然,引力的量子化方案也可以不是在广义相对论的范畴里打圈。
比如,彭加莱规范场论认为彭加莱群可以作为和规范场论中的各类李群一样的主丛结构,从而建立一套完全规范场论形式的彭加莱引力理论,其和广义相对论在某种程度上也是非常接近的。
我们还可以再进一步扔掉一些假定。
比如,我们可以扔掉前面三个假定的第一条,于是现在时空点的邻域就可以非常任意了,和闵氏时空可以完全不同。
而,我们知道闵氏时空的特点就是各向同性与处处相等,因此去掉这个假定后的最一般化的时空,就是特征速度非但在不同点上是不同的,在不同方向上也是不同的,且这种不同无法通过坐标变换来消除。
于是,这就是一个赝Finsler时空。
嗯,我又开始扯淡了……
好了,今天的睡前说就讲到这里。
我们这次将的主要内容可以看作是在已经知道时空到底是怎么个扭曲法的前提下(也就是知道了度规张量),物质在上面究竟是怎么运动的(当然我们只考虑点粒子,非点粒子的话就会有潮汐力,这个也很有意思)。可以说是时空中物质的运动学。
广义相对论还有另一大部分的内容,是物质作用下时空的运动学,也就是物质是如何影响时空的扭曲与形变的,这个下次再说。
嗯,本周任务完成了,欧耶~~~
本文遵守创作共享CC BY-NC-SA 4.0协议
通过本协议,您可以分享并修改本文内容,只要你遵守以下授权条款规定:姓名标示 、非商业性、相同方式分享。
具体内容请查阅上述协议声明。
本文禁止一切纸媒,即印刷于纸张之上的一切组织,包括但不限于转载、摘编的任何应用和衍生。网络平台如需转载必须与本人联系确认。
如果喜欢,想要下载App的话,轻戳这里~~
私人推荐订阅专题:《有意思的文章》、《严肃码匠圈》