难度最大最强。算法题拉开分数最大。比如阿里,特别强调算法题。如果业务对算法要求比较高,算法一定要准备。尤其金融方面。比如阿里云。不同岗位准备的东西是不一样的。算法基本功要准备的。
链表js实现难度比较大。递归是必要的。
加一个冒泡排序。一般不会让你写,但是会题目中某一步可能含得有排序。
终止条件和参数传递比较重要。知道用递归,不等于会写。
时间不足,这个可以放弃。遇到了,至少知道思路是什么。理论知道了,源码写不出来,至少能写出一部分了。
实在没打答上了,第一上面基本功要掌握。第二,拿到题目,要理解题目意思。你实在不理解,你可以请教面试官,可不可以给我一些提示?面试官有义务给你提示。如果你前面回答的太烂了,他可能不太愿意提示你。前面东西掌握了,然后思考这题,是用排序啊,递归啊,还是堆栈,已经有思路了。然后可以发挥了。不知道代码怎么写,然后用伪代码。然后分解,能想到哪,就写到哪。写到某一步,比如某个api实在想不出来,可以问面试官。你如果说这个题实在不知道怎么答了,但是你要告诉他这个原理怎么写,核心原理,在哪看过,什么思路。 真的面的算法太难,可能招的不是做前端的。
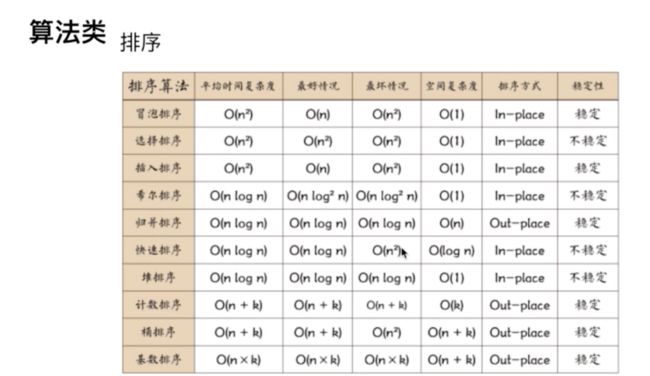
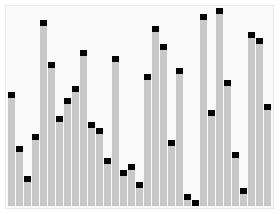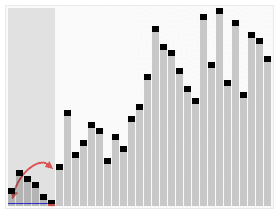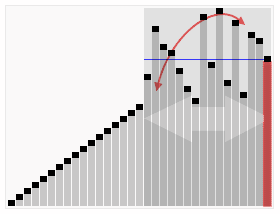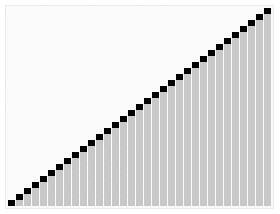
各种排序如下:
1. 快速排序
1.1 算法描述
快速排序由于排序效率在同为O(N*logN)的几种排序方法中效率较高,因此经常被采用,再加上快速排序思想----分治法也确实实用。快速排序是一种既不浪费空间又可以快一点的排序算法。
1.2 算法步骤
先从数列中取出一个数作为“基准”。
分区过程:将比这个“基准”大的数全放到“基准”的右边,小于或等于“基准”的数全放到“基准”的左边。
再对左右区间重复第二步,直到各区间只有一个数。
2. 选择排序
1.1 算法描述
选择排序是一种简单直观的排序算法,无论什么数据进去都是O(n2) 的时间复杂度。所以用到它的时候,数据规模越小越好。唯一的好处可能就是不占用额外的内存空间了吧。通俗来说就是你们中间谁最小谁就出列,站到队列的最后边,然后继续对着剩余的无序数组说你们中间谁最小谁就出列,站到队列的最后边,一直到最后一个,继续站到最后边,这样数组就有了顺序,从小到大。
1.2 算法步骤
在未排序序列中找到最小(大)元素,存放到排序序列的起始位置
从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
重复第二步,直到所有元素均排序完毕。
1.3 算法实现
javascript语言实现
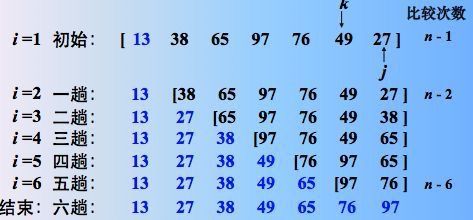
3. 希尔排序
1.1 算法描述
希尔排序,也称递减增量排序算法,是插入排序的一种更高效的改进版本。但希尔排序是非稳定排序算法。
希尔排序是基于插入排序的以下两点性质而提出改进方法的:
插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率;
但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位;
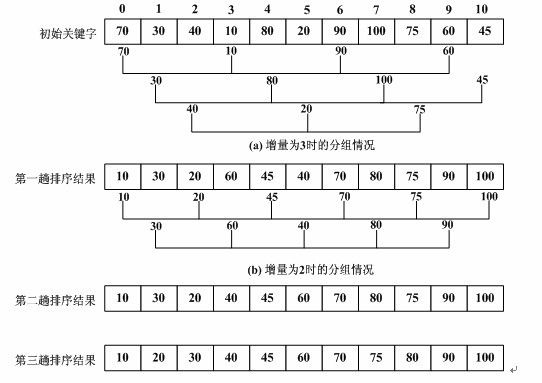
希尔排序的基本思想是:先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录基本有序时,再对全体记录进行依次直接插入排序。
1.2 算法步骤
选择一个增量序列 t1,t2,……,tk,其中 ti > tj, tk = 1;
按增量序列个数 k,对序列进行 k 趟排序;
每趟排序,根据对应的增量 ti,将待排序列分割成若干长度为 m 的子序列,分别对各子表进行直接插入排序。仅增量因子为 1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。
1.3 算法实现
波兰式、逆波兰式与表达式求值
波兰式、逆波兰式是《数据结构》课程中讲解关于栈的时候提到的,栈是很简单的一种数据结构。但是这些理论的提出却是计算机早期发展领域的重大突破,值得仔细回味。
1. 中缀表达式
我们在数学中学到的表达式被称为中缀表达式,操作符号在操作数中间,比如2 + 3 * (5 - 1)。对人类而言,这种表达方式显而易见,求值也很直接,先算乘除再算加减,先算括号内再算括号外。
然而,这个表达式对于计算机而言却很费解。你可能会有疑问:这有什么难理解的嘛,在JavaScript、Python或者Ruby,甚至是Java里面都可以通过eval("2 + 3 * (5 - 1)")来计算这个表达式。当然,这里的计算机并不是指现而今强大的计算机和高级编程语言,而是指上个世纪中页还处于发展初期的计算机。
2. 前缀表达式
早在1920年,波兰科学家扬·武卡谢维奇就发明了一种不需要括号的表示法,可以用来表示一个计算表达式。即将操作符号写在操作数之前,也就是前缀表达式,即波兰式(Polish Notation, PN)。这种表达式直到1960年计算机出现后才发挥出其威力。
比如2 + 3 * (5 - 1)这个表达式的前缀表达式为+ 2 * 3 - 5 1来表示。
阅读这个表达式需要从左至右读入表达式,如果一个操作符后面跟着两个操作数时,则计算,然后将结果作为操作数替换这个操作符和两个操作数,重复此步骤,直至所有操作符处理完毕。从左往右依次读取,直到遇到- 5 1,做计算后,将表达式替换为+ 2 * 3 4,然后从左往右再次读取,直到遇到* 3 4,做计算后将表达式替换为+ 2 12,然后从左往右依次读取,读到+ 2 12,计算得到14,到此结束。
可以看到,这种计算过程也相当复杂,需要多次遍历表达式,而且需要识别一个操作符后面跟着两个操作数这种模式,相比而言,下文中的逆波兰式要更为直接和简单。
如果你熟悉各种编程语言的话,这很像Lisp语言中的表达式(如下代码)。需要注意的是,Lisp语言中的括号并不是数学意义上的的括号,Lisp中的函数是可以携带多个参数的,比如(+ 1 2 3),因此需要使用括号来标明函数参数。
Clojure1.5.1user=>(+2(*3(-51)))14
3. 后缀表达式
后缀表达式也称为逆波兰式(Reverse Polish Notation, RPN),更加广为人知一些,和前缀表达式刚好相反,是将操作符号放置于操作数之后,比如2 + 3 * (5 - 1)用逆波兰式来表示则是:2 3 5 1 - * +。
逆波兰式的计算也是从左往右依次读取,当读到操作符时,将之前的两个操作数做计算,然后替换这两个操作数和操作符,接着读取,重复此步骤。对于这个表达式,读到5 1 -,得到4,然后读取乘号,取出前面的3和上一步的计算结果4,并计算,到12,接着读取加号+,计算2 12 +得到14,计算结束。
上面这个步骤可以很容易的用栈来实现:
从左往右依次读取表达式,如果是数字则将该数字压栈,如果是符号,则将之前的两个数字出栈,做计算后,将计算结果压栈,直到表达式读取结束。栈中剩下的一个数就是计算结果。
逆波兰式看起来像波兰式反过来,比如5 + 1的波兰式是+ 5 1,逆波兰式为5 1 +或者1 5 +。也很明显,逆波兰式并不是简单的将波兰式反过来,因为,减法和除法中减数和被减数、除数与被除数是不能交换的,即- 10 5和- 5 10就完全不一样。
4. 中缀表达式到后缀表达式的转换
因为通过后缀表达式来进行计算只需要一个栈即可,从硬件和软件上实现都是极为便利的,因此逆波兰式在计算机领域的应用更加广泛,因此将中缀表达式转换为逆波兰式非常重要。
依然仅仅使用栈就可以将中缀表达式转换成逆波兰式,转换过程如下:
从左往右遍历中缀表达式中的每个数字和符号,弱是数字就输出,成为逆波兰式的一部分; 如果是右括号,或者是其他符号并且比当前栈顶符号的优先级低,则栈顶元素依次出栈并输出; 然后将当前符号进栈,重复以上操作直到结束。
还是以2 + 3 * (5 - 1)为例:
首先读入数字2,直接将其输出,输出为2,栈为空
接着读入加号+,由于栈为空,因此将其进栈,输出为2,栈为+
接着读入数字3,直接将其输出,输出为2 3,栈为+
接着读入乘号*,比栈顶元素优先级高,进栈,输出为2 3,栈为+ *
读入左括号(,直接进栈,输出2 3,栈为+ * (
读入数字5,直接将其输出,输出为2 3 5,栈为+ * (
读入减号-,栈顶元素为左括号,进栈,输出为2 3 5,栈为+ * ( -
读入数字1,直接将其输出,输出为2 3 5 1,栈为+ * ( -
读入右括号,依次输出栈顶元素,直到左括号,括号不输出,输出2 3 5 1 -,栈为+ *
已经无元素可读,依次输出栈顶元素,直到栈为空,输出2 3 5 1 - * +,栈为空
这样可以仅仅使用栈,首先将中缀表达式转换为逆波兰式,然后用本文第3节中的方法对后缀表达式进行求值,整个过程使用栈来完成即可。
5. 表达式树与逆波兰式
还可以通过另外一种方法来将一个表达式转换成波兰式和逆波兰式,这种方法依赖与树,首先需要根据表达式构建成树,仍然以2 + 3 * (5 - 1)为例,下图是其表达式树。
我们发现这个树的后序遍历结果为2 3 5 1 - * +,刚好是其逆波兰式;而其先序遍历结果为+ 2 * 3 - 5 1刚好为其波兰式;中序遍历就不用说了,就是我们常见的中缀表达式。我们也可以通过这种特性来实现表达式的各种表示方法的转换。
6. 参考
逆波兰表示法
波兰表示法
调度场算法
将表达式转换成逆波兰式
链表,队列,栈相关算法
https://juejin.im/entry/58759e79128fe1006b48cdfd