在集成学习(Ensemble Learning)中除了Bagging和Boosting对数据的横向划分划分之外,还有一个纵向划分(加深)的方法, 一般称为Stacked Generalization(SG)的技术。 SG这个技术已经在Kaggle竞赛中多次崭露头角了, 部分情况下,应用SG技术可以让错误率进一步降低30%。
什么是SG?
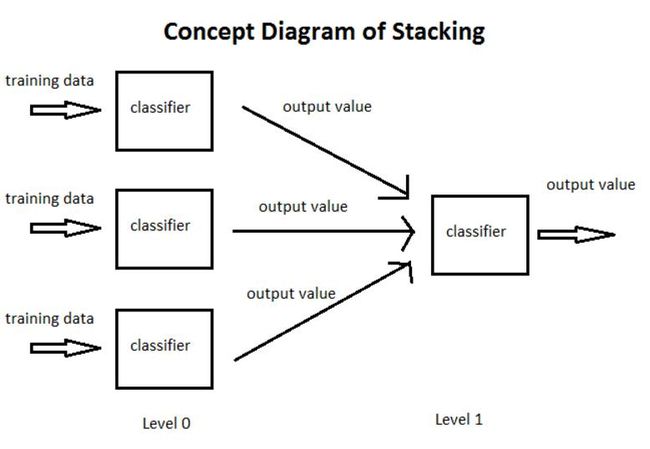
为了阐述, 下面借用了一张很直观的SG的示意图: 数据划分的纵向上有两层学习器, 把Level 0的Base-learner学习器的输出, 作为Level 1学习器的输入, Level 1的学习器又被称为Meta-learner或者Generalizer。 这种集成学习方式就是SG, 也称为Stacking。
SG是怎么诞生的?
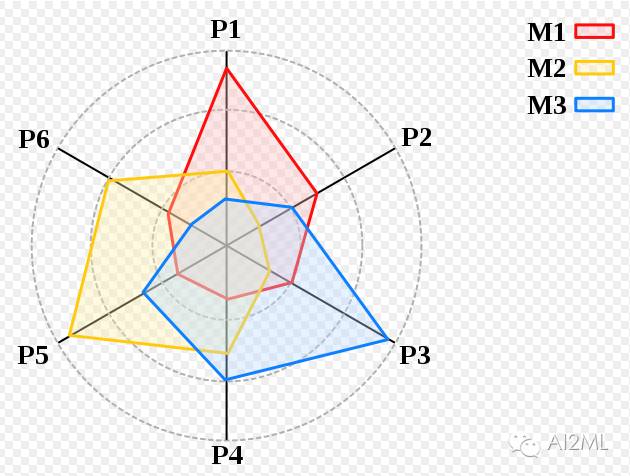
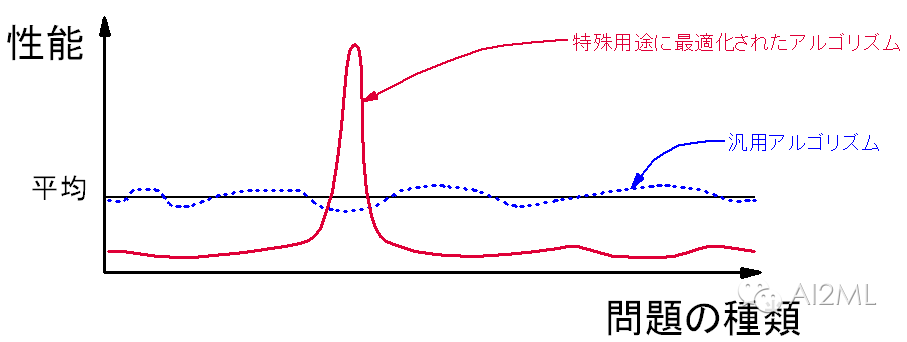
最早重视并提出Stacking技术的是David H. Wolpert,他在1992年发表了SG技术论文:这好比是巧妙的扩展了交叉验证(cross-validation), 通过胜者全得(winner-takes-all)的方式来集成的方法。 Wolpert大神是一个三栖学者, 数学家, 物理学家, 和计算学家。 他更为成名的是1995年提出No-Free-Lunch(NFL)理论。 NFL理论很直观,就是算法差异更多在于适不适合你要解决的问题。 比较多个算法, 例如,问题P1和机器学习M1合适, 但是不可能合适所有的问题。
Wolpert
多个算法的NFL解释
两个算法的NFL解释
也许NFL是对SG技术有效性更深层次思考的一种解释:如何协调不同的算法的适用性呢? SG就是这么一种有效的技术。
SG的基因?
SG是Ensemble Learning中异源集成(heterogenous ensembles)的典型代表。一般来说,同源集成(homogenous ensembles)就是Bagging和Boosting了(还有一个Cascading 的小众集成学习方法, 也可以算是同源集成)。
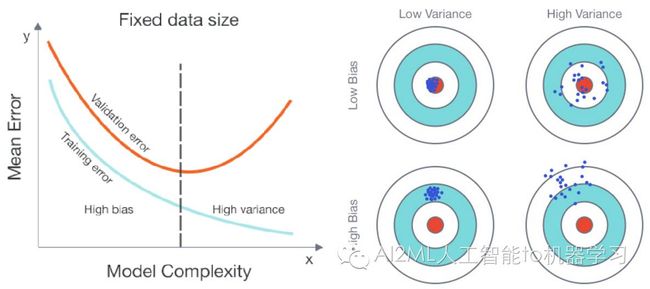
Bias-Variance平衡是机器学习的经典话题, 而集成学习就是在尽量不增加一方, 想法设法降低另外一方, 或者同时降低两者的方法, 而代价就是集成。
一句话, Stacking的基因就是Ensemble中Aggregation方法进一步泛化的结果, 是通过Meta-Learner来取代Bagging和Boosting的Voting/Averaging来综合降低Bias和Variance的方法。 譬如: voting可以通过KNN来实现, weighted voting可以通过softmax(Logistic Regression), 而averaging可以通过线性回归来实现。
Bagging, Boosting和Stacking的差异?
借用三张清晰的比较Bagging,Boosting, 和Stacking的示意图, 如下:
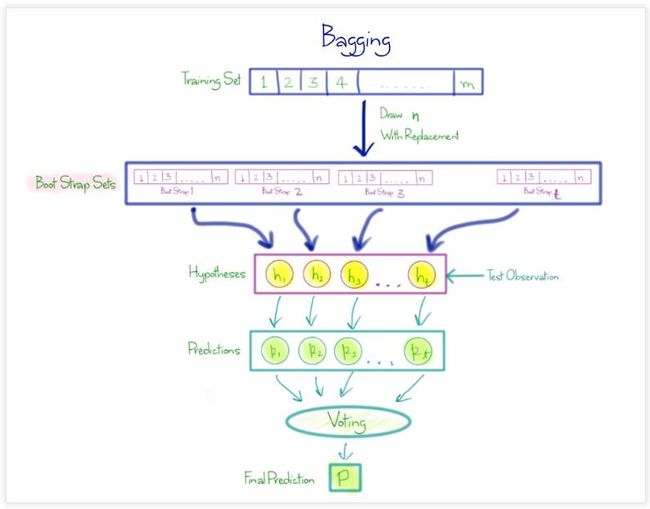
Bagging有一个Bootstrap的数据准备过程, 然后每份数据会学习出一个学习器, 然后基于这组学习的输出结果进行Voting或者Averaging,整个流程可以并行(Parallel)处理。
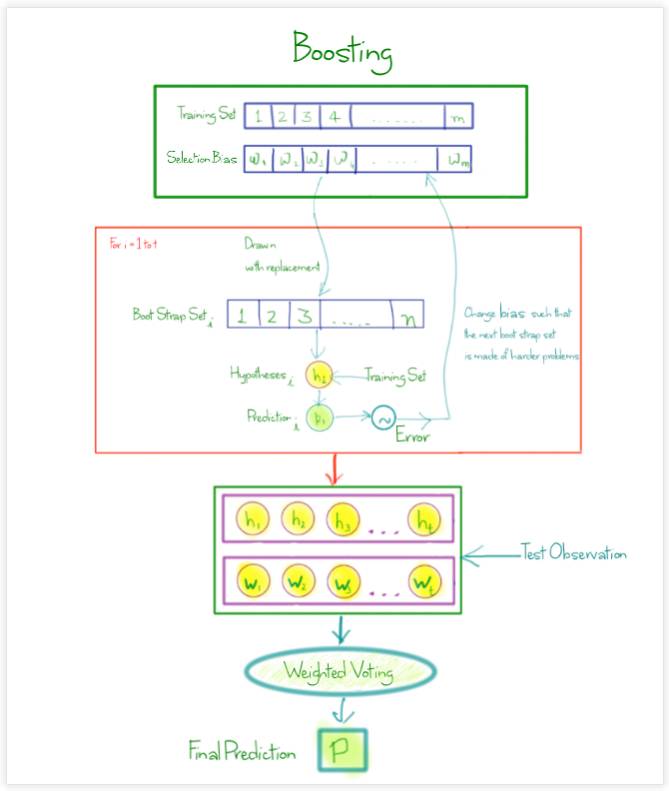
Boosting 根据当前学习器的错误率(Error Rate)来对数据进行筛选, 然后基于高错误率的数据再训练新的学习器,同时调整已有学习器的权重。 最后通过带权重的投票(Weighted Voting)来分类, 整个过程是有依赖顺序(Sequential)的。
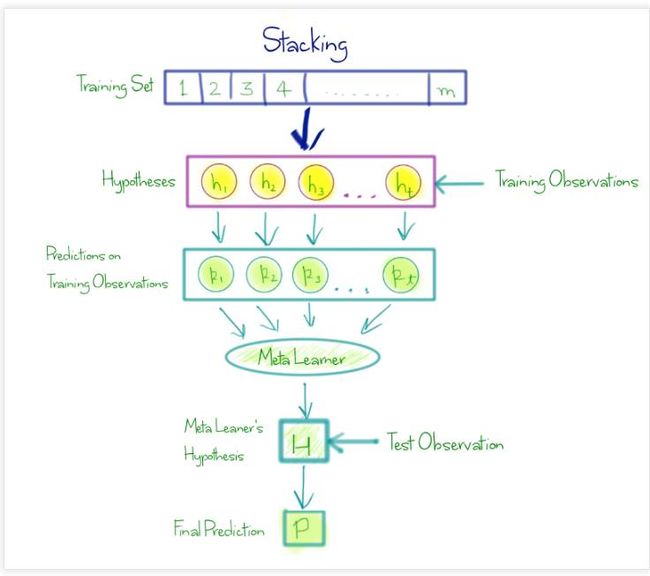
Stacking是先设好学习器base-learner, 然后把base-learner的输出作为meta-learner的输入进行集成。 这个框架简单,但是灵活度很高。
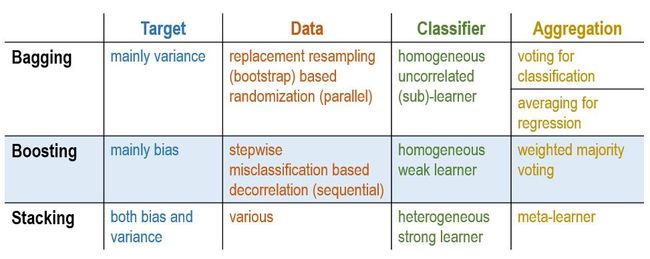
下面,总结下它们在目标, 数据, 分类器和集成方式等方面的差异:
其实, Stacking具有的灵活和不确定性,使得它既可以来实现Bagging方式, 又可以来实现Boosting方式。
SG是如何长成的?
理论方面,SG被Wolpert在1992年提出后,Leo Breiman这个大神, 在1996年把广义线性模型(Generalized Linear Model)和SG方法结合起来提出了 "Stacked Regressions"。 再之后,同样来自伯克利(Berkeley)的Mark J. van der Laan在2007的时候在表述Super Learner的时候, 从理论上证明了Stacking方法的有效性。
实践方面, 除了SG理论本身的突破之外, SG应用的广度和深度也在不停的突破, 其中一个是训练数据的分配(Blending的出现); 而另外一个是深层(3层以上)Stacking的出现。
Blending是一个简单模式, 除了最后一层一个Generalizer之外, 其他每层都是一组学习器, 然后两层之间相互连接一个或者多个的Base-learner学习器。前面我们讲到Stacking的训练, 是把这个集成模型看出一个大的学习器, 进行Cross-Validation的训练。 但是Blending希望把数据按层进行划分训练, 例如:
2层的Blending, 就会拿90%训练输入层, 然后10%数据训练输出层。
3层的Blending, 就会拿70%训练输入层,20%训练中间层, 然后10%的数据训练输出层。
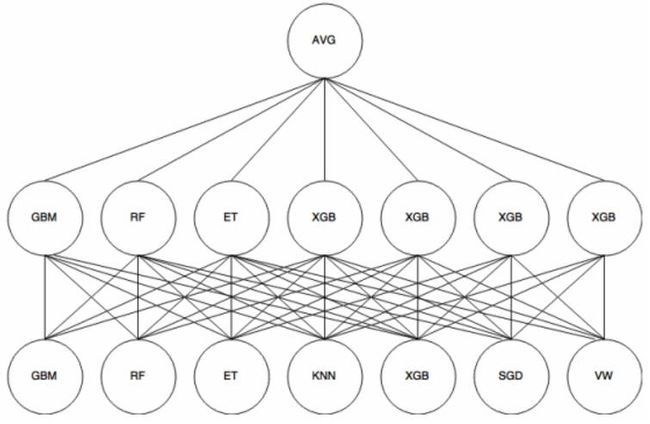
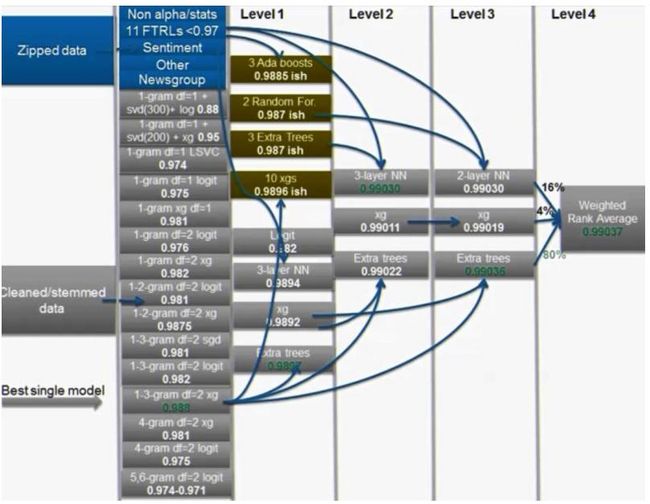
深度方面, Stacking也可以比较深(3层以上), 借用一个图示意如下:
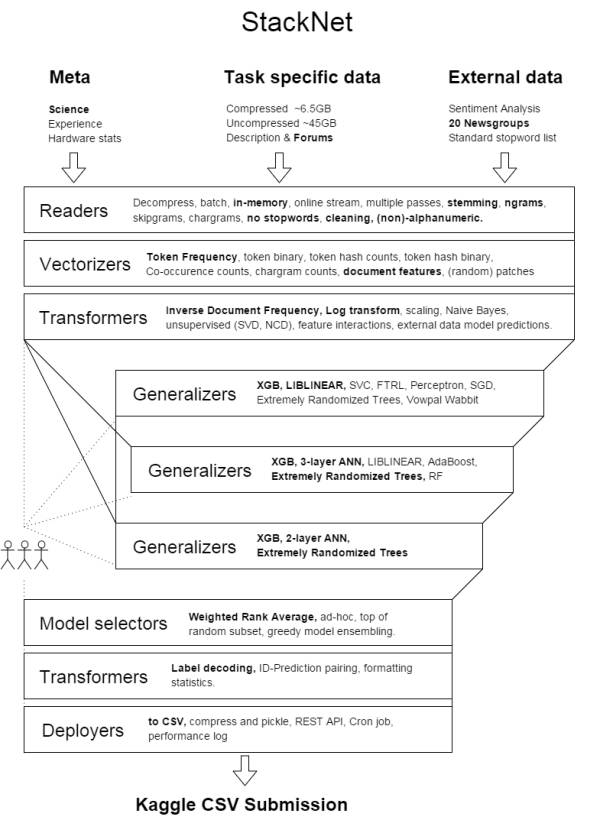
除了上述两方面, 要搞定一个Stacked Generalization框架除了Stacking本身,其实还要做其他很多工作的。 如下图, 借用了别人解释的Kaggle竞赛中建立Stacking框架的概要Overview:
在上面这个图中, 除了列了各种操作, 还列了部分Stacking的Meta-learner, 例如XGB等, 那么有哪些常见的Meta-learner呢?
常见Meta-learner是?
SG的最后的meta-learner层很大程度是要矫正不同学习器之间的Bias。 因此它的选择是个很大的挑战。 早期人们在提如何设计meta-learner时候有两点要求: 1)meta-learner的输入最好是类别的概率,而不是直接类别的标签。 2)结合线性或者非线性回归的计算可以用来集成类别的概率。 下面列一下已经被用过的meta-learner。
1. 统计方法的Meta-Learner:
Voting ( Majority based, Probabilitybased)
Averaging (Weighted, Ranked)
2. 经典容易解释的机器学习算法:
Logistic Regression (LR)
Decision Tree (C4.5)
3. 非线性(non-linear)机器学习算法:
Gradient Boosting Machine (GBM,XGBoost),
Nearest Neighbor (NN),
k-Nearest Neighbors (k-NN),
Random Forest (RF)
Extremely Randomized Trees (ERT).
4. 加权一次/二次线性(Weighted Linear / Quadratic)模型
Feature weighted linear stacking
Quadratic - Linearstacking
5. Multiple response 分析(非线性)框架
Multi-response linear regression (MLR)
Multi-response model trees (MRMT)
6. 无监督(Unsupervised)方法
- 聚类 Clustering
K-Means
Unsupervised Hierarchical Weighted Multi-segmenter
-维度压缩 Dimension Reductoin
t-Distributed Stochastic Neighbor Embedding (t-SNE)
7. 其他, 在线学习, 神经网络,遗传学习, 群体智能 等:
-在线学习 Online stacking (OS)
Linear perceptron with online random tree
Random bit regression (RBR)
Vowpal Wabbit (VW)
Follow the Regularized Leader (FTRL)
-神经网络Artificial neural network (ANN)
2 layer - ANN
3 layer - ANN
-遗传学习 Genetic algorithm (GA)
GA-Stacking
-群体智能 Swarm intelligence (SI)
Artificial bee colony algorithm
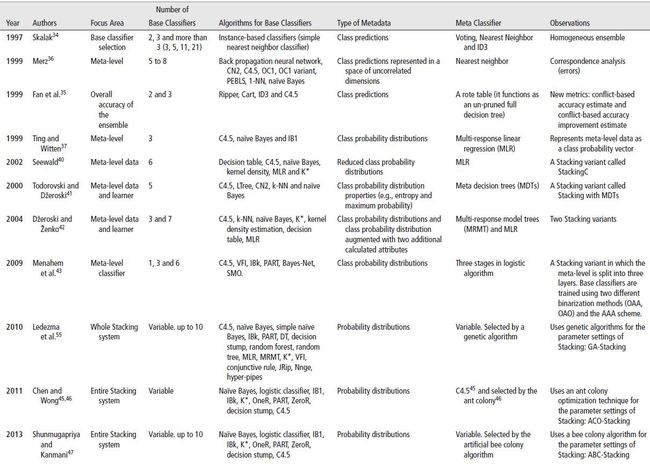
另外, 这有个文章列表显示从1997年到2013年, Meta-learner的设置越来越新颖广泛:
如何测试评价呢?
各种评价标准:
ACC: accuracy
RMS: root-mean-squared error
MXE: mean cross entropy
LFT: lift
BEP: precision/recall break-even point
FSC: precision-recall F score
APR: average precision
ROC: ROC / AUC
CAL: probability calibration
SAR: (ACC + ROC + (1 - RMS) ) / 3 (一种综合的稳定的评价标准)
综上, SG是很强大的集成方式, 某种意义上, 和深度学习类似, 纵向增加了学习深度, 但是也增加了模型复杂型和不可解释性。如何精心的选择Meta-learner 和 Base-learner, 训练方式, 评价标准等也是要重视的经验。
参考:
http://machine-learning.martinsewell.com/ensembles/stacking/
http://www.cs.utsa.edu/~bylander/cs6243/wolpert92stacked.pdf
http://www.santafe.edu/about/people/profile/David%20Wolpert
http://mlwave.com/kaggle-ensembling-guide/
http://www.chioka.in/stacking-blending-and-stacked-generalization/
http://manish2020.blogspot.my/2012_12_01_archive.html
http://blog.fliptop.com/blog/2015/03/02/bias-variance-and-overfitting-machine-learning-overview/
http://blog.kaggle.com/2015/12/03/dato-winners-interview-1st-place-mad-professors/
https://en.wikipedia.org/wiki/Cascading_classifiers
http://www.stata.com/support/faqs/data-management/multiple-responses/
http://gerardnico.com/wiki/data_mining/non_linear
http://puyokw.hatenablog.com/entry/2015/12/12/090000
http://qiita.com/sergeant-wizard/items/d1509f71943b429929cf
https://www.semanticscholar.org/paper/Issues-in-Stacked-Generalization-Ting-Witten/1c58b4c7adee37874ac96f7d859d1a51f97bf6aa
https://www.quora.com/What-are-the-different-ways-to-generalize-logistic-regression-to-multiple-class-labels-instead-of-only-binary
https://discuss.analyticsvidhya.com/t/stacked-generalization/2589
http://blog.csdn.net/u014114990/article/details/50819948
https://www.52ml.net/19553.html
https://github.com/dustinstansbury/stacked_generalization
http://www.tuicool.com/articles/IJza2ij
https://my.oschina.net/airxiechao/blog/755899
http://www.emeraldinsight.com/doi/abs/10.1108/14684520310510091