目录
- 1. 案例
- 2. APDL分析
1. 案例
一个温度为300℃的铜环和一个温度为200℃的铁环,放置到22℃的水中进行淬火。水桶为铁质的圆形。分析中忽略水的流动。
材料参数
| 热性能 | 铜 | 铁 | 水 |
|---|---|---|---|
| 导热系数(W/(m℃) | 383 | 70 | 0.61 |
| 密度(kg/m3 | 8889 | 7833 | 996 |
| 比热容(J/(kg.℃) | 390 | 448 | 4185 |
因为忽略了水的流动,故可将水看为一种材料,直接进行分析
2. APDL分析
finish
/clear
!==============第一步:进行稳态二维轴对称分析===============================
/filname,quench
/prep7
et,1,plane55 ! 选择单元类型
keyopt,1,3,1 ! 设置为轴对称分析
! 定义材料热性能参数
mp,kxx,1,383
mp,dens,1,8889
mp,c,1,390 ! 定义铜的热物理性能参数
mp,kxx,2,70
mp,dens,2,7837
mp,c,2,448 ! 定义铁的热物理性能参数
mp,kxx,3,0.61
mp,dens,3,996
mp,c,3,4185 ! 定义水的热物理性能参数
rectng,0,0.08,0,0.01
rectng,0.08,0.1,0,0.01
rectng,0.1,0.12,0,0.01
rectng,0.12,0.14,0,0.01
rectng,0.14,0.15,0,0.01
rectng,0.14,0.15,0.01,0.055
rectng,0.14,0.15,0.055,0.1
rectng,0.14,0.15,0.1,0.15 ! 建立铁箱矩形
rectng,0.08,0.1,0.01,0.055
rectng,0.1,0.12,0.01,0.055 ! 建立铜环
rectng,0.08,0.1,0.055,0.1 ! 建立铁环
rectng,0,0.08,0.01,0.055
rectng,0.12,0.14,0.01,0.055
rectng,0,0.08,0.055,0.1
rectng,0.10,0.12,0.055,0.1
rectng,0.12,0.14,0.055,0.1
rectng,0,0.08,0.1,0.15
rectng,0.08,0.1,0.1,0.15
rectng,0.10,0.12,0.1,0.15
rectng,0.12,0.14,0.1,0.15 ! 建立水几何模型
aglue,all ! 粘接各矩形
esize,0.003,0, ! 定义单元划分尺寸
asel,s,,,1,21,20
asel,a,,,23,29,1
aatt,2,1,1 ! 附于铁箱和铁环的材料属性
asel,s,,,30,33,3
aatt,1,1,1 ! 附于铜环的材料属性
asel,s,,,31,32,1
asel,a,,,34,39,1
asel,a,,,22
aatt,3,1,1 ! 附于水的材料属性
allsel,all
mshkey,2 ! 定义映射单元划分类型
amesh,all ! 划分单元
asel,s,,,1,21,20
asel,a,,,23,28,1
asel,a,,,31,32,1
asel,a,,,34,39,1
asel,a,,,22
nsla,,1
d,all,temp,20 ! 施加铁箱和水的温度约束条件
asel,s,,,30,33,3
nsla,,1
d,all,temp,300 ! 施加铜环的温度约束条件
asel,s,,,29
nsla,,1
d,all,temp,200 ! 施加铁环的温度约束条件
allsel,all
/solu
antype,trans ! 设定为瞬态分析
timint,off ! 关掉时间积分, 即设定为稳态分析
time,0.01 ! 设定只有一个子步的时间很小的载荷步
deltim,0.01 ! 设定求解时间子步
solve ! 求解
!==============第二步:进行瞬态二维轴对称分析===============================
time,3600 ! 设定求解时间
timint,on ! 打开时间积分
deltim,26,2,200 ! 设置时间步长,最大及最小时间步长
autots,on ! 打开自动时间步长
ddelet,all,temp ! 删除稳态分析中定义的节点温度
outres,all,1 ! 将每个子步的值写入数据库文件
solve ! 求解
finish
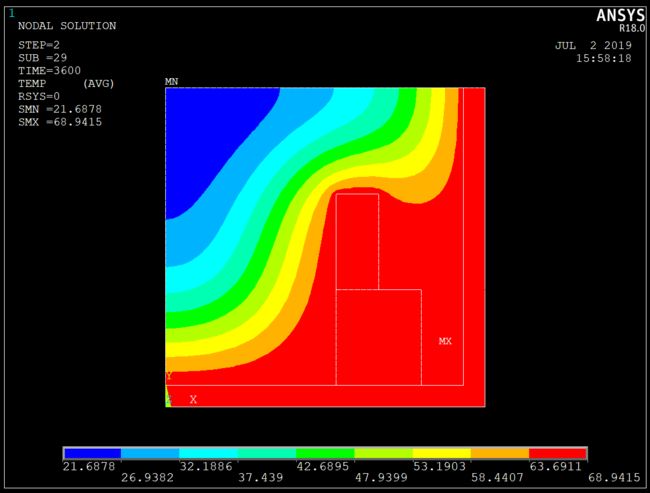
/post1
plnsol,temp,,0