今天,我们来学习如何设计自定义位置的相机
ready
我们只需要了解我们之前的坐标体系,或者说是相机位置
先看效果
Chapter10:Positionable camera
这一章我们直接用概念贯穿整章
1.fov: field of view
它是一个角度
它分为两种:垂直方向岔开的角度(vfov)和水平方向岔开的角度(hfov)
vfov即相机在垂直方向上从屏幕顶端扫描到底部所岔开的视角角度
hfov即相机在水平方向上从屏幕左端扫描到右端所岔开的视角角度
2.aspect:屏幕宽高比
我们之前是通过直接定义屏幕的坐标位置来确定屏幕,现在,我们可以通过相机参数来确定屏幕
目前,我们暂时还用ready中的坐标,相机在原点,屏幕中心在(0,0,-1)
我们习惯采用vfov,这里我们假设一直vfov和aspect
眼睛离屏幕中心的距离为dis(也就是1)
根据 tan(vfov/2) = (屏幕高/2)/dis
得到 屏幕高 = 2 * dis * tan(vfov/2)
则,屏幕上边界为 y_up = dis * tan(vfov/2)
屏幕下边界为 y_bottom = - y_up
屏幕宽 = 屏幕高 * aspect
则,屏幕左边界为 x_left = - 屏幕宽/2
屏幕右边界为 x_right = - x_left
所以,我们目前的相机类如下:
/// camera.h // ----------------------------------------------------- // [author] lv // [begin ] 2019.1 // [brief ] the camera-class for the ray-tracing project // from the 《ray tracing in one week》 // ----------------------------------------------------- #ifndef CAMERA_H #define CAMERA_H #include "ray.h" namespace rt { class camera { public: camera(rtvar vfov, rtvar aspect) :_eye(rtvec(0.,0.,0.)) { rtvar theta = vfov * π / 180; rtvar half_height = tan(theta / 2); rtvar half_width = aspect * half_height; _start = rtvec(-half_width, -half_height, -1.0); _horizontal = rtvec(2 * half_width, 0., 0.); _vertical = rtvec(0., 2 * half_height, 0.); } inline const ray get_ray(const rtvar u,const rtvar v)const { return ray{ _eye, _start + u*_horizontal + v*_vertical }; } inline const ray get_ray(const lvgm::vec2& para)const { return ray{_eye, _start + para.u()*_horizontal + para.v()*_vertical}; } inline const rtvec& eye()const { return _eye; } inline const rtvec& start()const { return _start; } inline const rtvec& horizontal()const { return _horizontal; } inline const rtvec& vertical()const { return _vertical; } private: rtvec _eye; rtvec _start; //left-bottom rtvec _horizontal; rtvec _vertical; }; } #endif
同时,我们如下设置main的相关数据,先来测试一下
Lambertian(rtvec(0,0,1))过滤red和green,完全保留blue
没问题吧,屏幕宽为4,高为2,两边少的部分是被视锥体切掉了
从原点往左右边界连线,左三角面和右三角面内的部分才可见
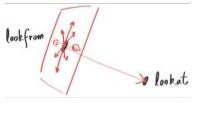
3.lookfrom:相机所在位置
4.lookat:相机视线指向的位置点
相机在lookfrom位置看向lookat点
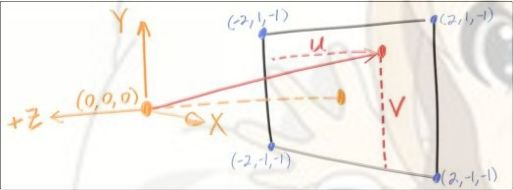
5.相机平面
相机平面是过lookfrom垂直于视线(from->at)的一个平面
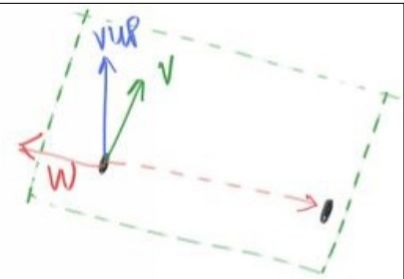
类似于坐标系,确定平面当然也需要正交基向量,而相机三维正交基一般采用uvw坐标系
一个个描述
在阐述uvw之前先确定一个正向上的向量,因为相机坐标系算是一个局部性质的,当我们把它放在世界坐标系中,就需要用一个始终指向世界坐标系正上方的基向量vup(view up)
我们现在来确定三维正交相机坐标系
我们先来确定w,w是一个正交于相机平面的基向量
它的定义为 w = lookfrom - lookat
有了w,我们便可以定义u了,u向量代表相机平面的水平向量
u一定平行于世界坐标系的x轴
vup平行于世界坐标系的y轴
所以u⊥vup
而w⊥相机平面,所以w⊥u
所以 u = vup × w 该体系为右手系
最后定义v,v就是相机平面的垂直方向
即, v = w × u
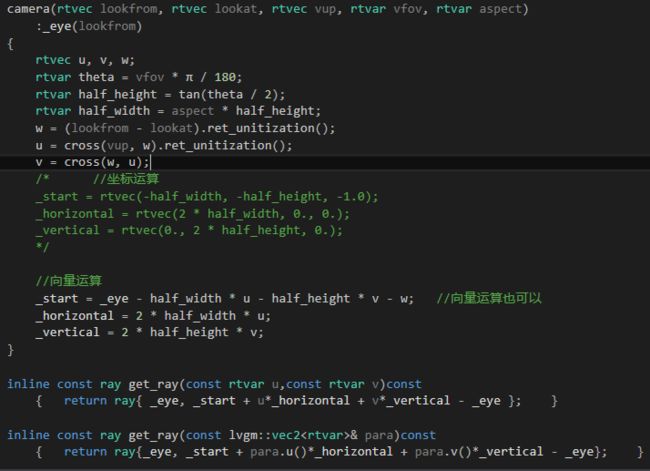
所以,我们可以定义一个完整的camera类啦
构造函数改动如下:
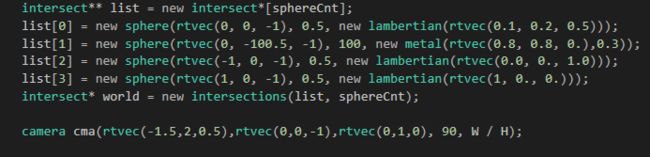
我们试着,站在(-2,2,1)位置,往屏幕中心(0,0,-1)看
它应该是一张俯瞰图
主函数:
如图:
左边的金属球只反射光蓝色分量,右边的漫反射球只反射光的红色分量
至于蓝色的金属球下部是黑色的,只能解释为下部的反射光中蓝色成分比较少
所以,过了这一节,我们的镜头就可以远近上下左右调整了,屏幕也随时跟着相机动,为相机影像做投影
是不是非常激动
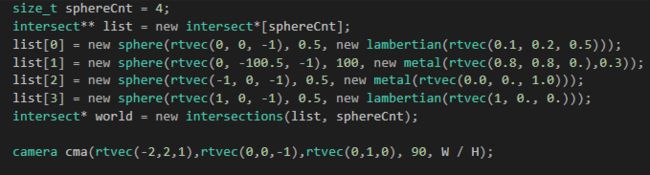
前面那张效果图是如下设置的,球的性质改了一下,且把相机拉近了些(感觉书上的距离太远了)
感谢您的阅读,生活愉快~