张三木教你理解回溯法

回溯法

回溯法（搜索与回溯法）是一种选优搜索法，又称为试探法，按选优条件向前搜索，以达到目标。但当搜索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择。这种走不通就退回再走的技术为回溯法。而满足回溯条件的某个状态的点称为“回溯点”。

回溯法问题的框架

问题的解空间

复杂问题常常有很多的可能解，这些可能的解构成了问题的解空间。解空间就是进行穷举的搜索空间，所以解空间中应该包含所有的可能解，且至少应该包含问题的一个最优解。例如：对于有n个物品的0/1背包问题，当n=3时，其解空间是：{(0, 0, 0), (0, 0, 1), (0, 1, 0), (1, 0, 0), (0, 1, 1), (1, 0, 1), (1, 1, 0), (1, 1, 1) }。

回溯法的基本思想

基本步骤

1. 针对所给的问题，定义问题的解空间
2. 确定易于搜索的解空间结构
3. 以深度优先方式搜索解空间，并且在搜索过程中用剪枝函数避免无效搜索

常用剪枝函数

1. 约束函数：减去不满足条件的子树
2. 限界函数：减去得不到最优解的子树

递归和迭代回溯

递归回溯

模板：

void Backtrack( int t ){
    if ( f > n ) {
        Output(x);
    }else{
        for( int i = f(n,t), i<=g(n,t);i++){
            x[t] = h(i);
            if(Constraint(t)&&Bound(t)){
                Backtrack(t+1);
           }
        }
    }    
}       

迭代回溯

模板：

void IterativeBacktrack(void){
    int t=1;
    while(t>0){
        if(f(n,t)<=g(n,t){
            for(int i=f(n,t);i<=g(n,t);i++){
                x[t]=h(i);
                if(Constraint(t)&&Bound(t)){
                    if(Solution(t))
                        Output(x);
                   else
                       t++;
                  }
          else
            t--;
          }
      }
  }         

子集树和排列树

• 子集树：当所给的问题是从n个元素的集合S中找出满足某种性质的子集时，相应的解空间为子集树。如0-1背包问题。
• 排列树：当所给问题是确定n个元素的满足某种性质的排列时，相应的解空间为排列树。如旅行售货员问题。

经典例题

子集和问题

题目：

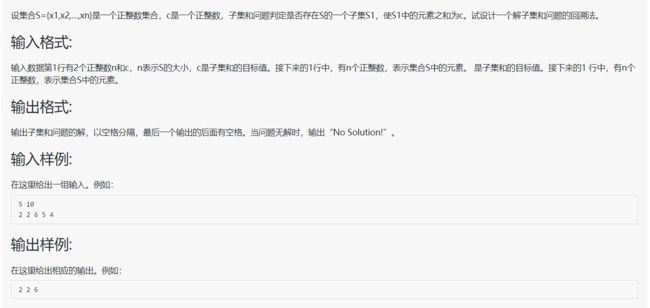
解析：
该题的解空间是一个子集树，其中解集为S={s1,s2,··,sn}，s1到sn的和为给定的C。同样，为了避免无效搜索，加快算法效率，需要剪枝函数。该题的剪枝函数限制条件为当前已加的值sum加上当前结点的值value大于给定的C，则不往下遍历。（这里没有做剪枝，丢人）
代码如下：

#include
using namespace std;
#define MAXLENGTH 10005
int arr[MAXLENGTH]; // 存储数组
bool haveUsed[MAXLENGTH]; // 存储数组各个元素当前状态
int value; // 存储当前值
bool isPrint = false;

void count(int i,int num,int sum) {
    if (i > num||isPrint) {
        return;
    };
    haveUsed[i] = true;
    value += arr[i];

    if (value == sum&&!isPrint) {
        for (int j = 0; j < num; j++) {
            if (haveUsed[j]==true) {
                cout << arr[j]<<" ";
            }
        };
        isPrint = true;
        return;
    }
    else if(value> num >> sum;
    for (int i = 0; i < num; i++) {
        cin >> arr[i];
        tmp += arr[i];
    }
    if (tmp < sum) {
        cout << "No Solution!" << endl;
        return 0;
    }
    count(0, num, sum);
    if (!isPrint) {
        cout << "No Solution!" << endl;
    }
    system("pause");
    return 0;
}

总结

1. 当问题是满足某种性质（约束条件）取得最优解时，往往采用回溯法。
2. 回溯法的实现方法有两种：递归和迭代。一个问题两种方法都可以实现，只是算法效率会有不一样。
3. 因为有剪枝函数，回溯法的效率远远大于穷举法。

结对编程状况

结对编程的时候我一般负责代码实现和提供思路，队友每次都能纠正我的思维盲点，以及提出高效的剪枝函数的条件。合作愉快。（反正就是被带飞了）