对二叉树进行先序、中序、后序遍历都是从根结点开始,且在遍历的过程中,经过的节点路线都是一样的,只不过访问的顺序不同。
先序遍历是深入时遇到结点就访问,中序遍历是深入时从左子树返回时遇到结点就访问,而后序遍历是从右子树反回时遇到根结点就访问,在这一过程中,反回结点的顺序与深入结点的顺序相反,即先深入再反回,这不禁让人联想到栈,而想要实现二叉树的非递归遍历,就需要用栈的思想来实现
先序遍历(DLR)
先序遍历的递归过程为
(1)访问根结点
(2)先序遍历根结点的左子树
(3)先序遍历根结点的右子树
而先序遍历的非递归过程为
先将根结点进栈,当栈不为空时,出栈并访问,然后依次将右左结点进栈(栈先进后出,所以先进栈右结点)
void NRPreOrder(Btnode *b)
{
Btnode *p;
SqStack st;
InitStack(st);
if (b != NULL)
{
Push(st, b); //根结点入栈
while (!StackEmpty(st))
{
Pop(st, p); //根结点出栈
printf("%c",p->data); //在此处用输出根接地那的值表示出栈
if (p->right != NULL) //当右子树非空
Push(st, p->right); //右孩子入栈
if (p->left != NULL) //当左子树非空
Push(st, p->left); //左孩子入栈
}
printf("\n");
}
DestroyStack(st);
}还有一种前序遍历的非递归方式:
沿左子树深入时,入栈之前访问该结点
继续深入,为NULL时,则返回并弹出前面压入的节点
从该结点的右子树继续深入
void NRPreOrder(BiTree t) //非递归先序遍历二叉树
{
BiTree stack[maxsize],p;
int top; //栈顶
if(t==NULL) return; //树为空则返回
top=0;
p=t; 这是一个用于存储移动的指针的变量
while(!(p==NULL&&top==0)) //当根结点不为空且栈不为空时
{
while(p!=NULL) //先深入左子树
{
printf("%2c",p->data); //在此处用打印表示访问该结点
if(top<=maxsize-1)
{
stack[top]=p; //入栈
top++; //栈顶位置++
}
else //栈满时
{
printf("栈溢出");
return;
}
p=p->lchild; //深入当前根结点的左子树
}
if(top<=0)return;
else
{
top--; //栈顶--,
p=stack[top]; //弹出栈顶元素
p=p->rchild; //指向右子树
}
}中序遍历(DLR)
而中序遍历的方法和1先序遍历极为相似,只是访问的时机不停,在这里就不重复说明啦,当然,如果哪位有问题的话,欢迎私聊

void NRPreOrder(BiTree t) //非递归先序遍历二叉树
{
BiTree stack[maxsize],p;
int top; //栈顶
if(bt==NULL) return; //树为空则返回
top=0;
p=bt; 这是一个用于存储移动的指针的变量
while(!(p==NULL&&top==0)) //当根结点不为空且栈不为空时
{
while(p!=NULL) //先深入左子树
{
if(top<=maxsize-1)
{
stack[top]=p; //入栈
top++; //栈顶位置++
}
else //栈满时
{
printf("栈溢出");
return;
}
p=p->lchild; //深入当前根结点的左子树
}
if(top<=0)return;
else
{
top--; //栈顶--,
p=stack[top]; //弹出栈顶元素
printf("%2c",&p->data); //在此处用打印表示访问该结点
p=p->rchild; //指向右子树
}
}当然,除此之外,个人在bilibili上看到一个很好的演示过程,在这里推荐给米娜桑 https://www.bilibili.com/video/av40285886?from=search&seid=17491349128453302359
后序遍历(DLR)
后序遍历的特殊性在于,结点第一次出栈之后,还需要再次入栈,即一个结点出两次入两次栈,那么,是否该打印该结点的值成为了一个问题。这不禁让我想到大一在做一个学生成绩管理系统时遇到还未学习链表等结构时对于学生成绩的删除方式。当时在创建学生类时,为其添加了一个变量叫做“alive”,每一个类的对象的“alive”初始属性都是1,当根据学号删除该学生时,该学生类的“alive”属性变为的0,这样,在输出、排序等操作所以学生的信息的时候,就不必再对“alive”属性为0的学生进行操作
所以,这个方法也可以运用在次数
在创建栈时,我们可以为栈中元素添加一个“flag”属性:

即:
typedef struct
{
BiTree link;
int flag;
}stacktype;函数代码:
void Nrpostorder(BiTree T)
{
stacktype stack[max];
BiTree p;
int top,sign;
if(T==NULL) return;
top=-1;
p=T;
while(!(p==NULL&&top==-1))
{
if(p!=NULL)
{
top++;
stack[top].link=p;
stack[top].flag=1;
p=p->lchild;
}
else
{
p=stack[top].link;
sign=stack[top].flag;
top--;
if(sign==1)
{
top++;
stack[top].link=p;
stack[top].flag=2;
p=p->rchild;
}
else
{
printf("%2c",p->data);
p=NULL;
}
}
}
} 最终代码:
#include
#include
#define MAX 20
typedef char TElemType;
typedef int Status;
typedef struct BiTNode
{
TElemType data;
struct BiTNode *lchild,*rchild; //左右孩子的指针
} BiTNode,*BiTree;
typedef struct
{
BiTree link;
int flag;
}stacktype;
//先序创建二叉树
void CreateBiTree(BiTree *T)
{
char ch;
ch=getchar();
if(ch=='#')(*T)=NULL; //#代表空指针
else
{
(*T)=(BiTree)malloc(sizeof(BiTNode)); //申请节点
(*T)->data=ch; //生成跟节点
CreateBiTree(&(*T)->lchild);
CreateBiTree(&(*T)->rchild);
}
}
//先序输出二叉树
void PreOrder(BiTree T)
{
if(T)
{
printf("%2c",T->data); //访问根节点,此处为输出根节点的数据值
PreOrder(T->lchild); //先序遍历左子树
PreOrder(T->rchild); //先序遍历右子树
}
}
//中序输出二叉树
void InOrder(BiTree T)
{
if(T)
{
InOrder(T->lchild);
printf("%2c",T->data);
InOrder(T->rchild);
}
}
//后序输出二叉树
void PostOrder(BiTree T)
{
if(T)
{
PostOrder(T->lchild);
PostOrder(T->rchild);
printf("%2c",T->data);
}
}
//先序非递归先序
int NRPreOrder(BiTree T) //非递归先序遍历二叉树
{
BiTree stack[MAX],p;
int top; //栈顶
if(T==NULL) return 0; //树为空则返回
top=0;
p=T; //这是一个用于存储移动的指针的变量
while(!(p==NULL&&top==0)) //当根结点不为空且栈不为空时
{
while(p!=NULL) //先深入左子树
{
printf("%2c",p->data); //在此处用打印表示访问该结点
if(top<=MAX-1)
{
stack[top]=p; //入栈
top++; //栈顶位置++
}
else //栈满时
{
printf("栈溢出");
return 0;
}
p=p->lchild; //深入当前根结点的左子树
}
if(top<=0) return 0;
else
{
top--; //栈顶--,
p=stack[top]; //弹出栈顶元素
p=p->rchild; //指向右子树
}
}
}
//中序非递归先序
int NRInOrder(BiTree T) //非递归先序遍历二叉树
{
BiTree stack[MAX],p;
int top; //栈顶
if(T==NULL) return 0; //树为空则返回
top=0;
p=T; //这是一个用于存储移动的指针的变量
while(!(p==NULL&&top==0)) //当根结点不为空且栈不为空时
{
while(p!=NULL) //先深入左子树
{
if(top<=MAX-1)
{
stack[top]=p; //入栈
top++; //栈顶位置++
}
else //栈满时
{
printf("栈溢出");
return 0;
}
p=p->lchild; //深入当前根结点的左子树
}
if(top<=0) return 0;
else
{
top--; //栈顶--,
p=stack[top]; //弹出栈顶元素
printf("%2c",p->data); //在此处用打印表示访问该结点
p=p->rchild; //指向右子树
}
}
}
//层次遍历二叉树
void LevelOrder(BiTree T)
{
BiTree Queue[MAX],b; //用一维数组表示队列,front和rear表示队首和队尾的指针
int front,rear;
front=rear=0;
if(T)
//若树为空
{
Queue[rear++]=T; //根节点入队列
while(front!=rear) //当队列非空
{
b=Queue[front++]; //队首元素出队列,并访问这个节点
printf("%2c",b->data);
if(b->lchild!=NULL) Queue[rear++]=b->lchild ; //若左子树非空,则入队列
if(b->rchild!=NULL) Queue[rear++]=b->rchild ; //若右子树非空,则入队列
}
}
}
//求树的深度
int depth(BiTree T)
{
int dep1,dep2;
if(T==NULL) return 0;
else
{
dep1=depth(T->lchild);
dep2=depth(T->rchild);
return dep1>dep2?dep1+1:dep2+1;
}
}
//后序非递归
void Nrpostorder(BiTree T)
{
stacktype stack[MAX];
BiTree p;
int top,sign;
if(T==NULL) return;
top=-1;
p=T;
while(!(p==NULL&&top==-1))
{
if(p!=NULL)
{
top++;
stack[top].link=p;
stack[top].flag=1;
p=p->lchild;
}
else
{
p=stack[top].link;
sign=stack[top].flag;
top--;
if(sign==1)
{
top++;
stack[top].link=p;
stack[top].flag=2;
p=p->rchild;
}
else
{
printf("%2c",p->data);
p=NULL;
}
}
}
}
int main()
{
BiTree T=NULL;
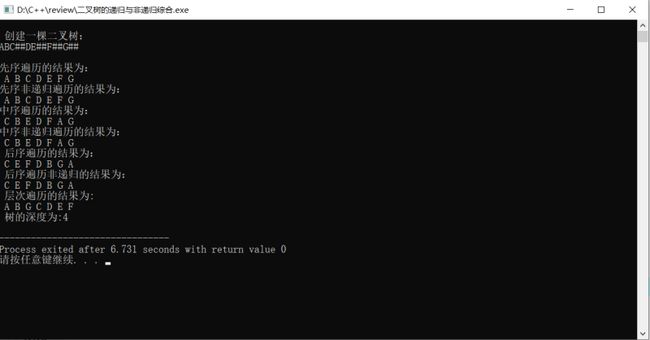
printf("\n 创建一棵二叉树: \n");
CreateBiTree(&T); //创建二叉树
printf("\n先序遍历的结果为:\n");
PreOrder(T); //先序遍历
printf("\n先序非递归遍历的结果为:\n");
NRPreOrder(T);
printf("\n中序遍历的结果为:\n");
InOrder(T); //中序遍历
printf("\n中序非递归遍历的结果为:\n");
NRInOrder(T); //中序遍历
printf("\n 后序遍历的结果为: \n");
PostOrder(T);
printf("\n 后序遍历非递归的结果为: \n");
Nrpostorder(T);
printf("\n 层次遍历的结果为: \n");
LevelOrder(T); //层次遍历
printf("\n 树的深度为:%d\n",depth(T));
}