昨天状态不是很好,没做出几个题,回到宿舍很早就睡了,今早4点半突然醒了,再也睡不着了,穿上衣服,简单洗刷之后就来到了图书馆...
打开Chrome,进入训练场,看到了这个:
我去,原来大家都这么努力,他俩一般是12点多刚打完球,然后平时1点还在补题...
不说了,肝!
今早,冷静下来,思考了当时没做出来的题,原来其实都那么“水”
这里提几个相对难一些的题目的题解,其它题可以私聊我QQ
只是相对难,其实还是蛮水的(逃...
问题 B:第N个智慧数
据说这个题,咱们队不约而同的打表,怪我...
不知道中石油张老师,看到我们工大的代码会怎么想...可怕...
#include
#include
#include
#include
#include
#include
using namespace std;
int n;
int num[200] = {3, 5, 7, 8, 9, 11, 12, 13, 15, 16, 17, 19, 20, 21, 23, 24, 25, 27, 28, 29, 31, 32, 33, 35, 36, 37, 39, 40, 41, 43, 44, 45, 47, 48, 49, 51, 52, 53, 55, 56, 57, 59, 60, 61, 63, 64, 65, 67, 68, 69, 71, 72, 73, 75, 76, 77, 79, 80, 81, 83, 84, 85, 87, 88, 89, 91, 92, 93, 95, 96, 97, 99, 100, 101, 103, 104, 105, 107, 108, 109, 111, 112, 113, 115, 116, 117, 119, 120, 121, 123, 124, 125, 127, 128, 129, 131, 132, 133, 135, 136, 137};
int main()
{
cin >> n;
cout << num[n - 1];
return 0;
}
问题 G:分割绳子
- 二分例题,套用我讲的二分模板就行
- 注意,这里变换区间的时候不是Left = mid + 1;而是Left = mid + 0.001;精度问题
- 其他地方也没得说,注意借用此题再巩固一下自己脑海中的二分思想
#include
#include
using namespace std;
double rope[1005];
int n, m;
double ans;
double mxn;
double l, r;
bool ansok(double k)
{
int s = 0;
for (int i = 0; i < n; i++)
{
s += rope[i] / k;
}
if (s >= m)
return true;
else
return false;
}
int main()
{
cin >> n >> m;
for (int i = 0; i < n; i++)
{
cin >> rope[i];
mxn = max(mxn, rope[i]);
}
l = 0;
r = mxn;
while (l <= r)
{
double mid = (l + r) / 2;
if (ansok(mid))
{
l = mid + 0.001;
ans = mid;
}
else
r = mid - 0.001;
}
printf("%.2f", ans);
return 0;
}
问题 K: 单纯质因数
- 这个题很多同学想打表,其实不用,看着数据,直接算应该没问题,我试了试,果然没问题
- 把一个数 num 分解质因数,同时质因数去重累乘得到 S 看 S 是否与sum相同,如果相同就表示这是一个单纯质因数
#include
#include
using namespace std;
bool isp(int num)
{
if (num == 1)
return 0;
if (num < 4)
return 1;
for (int i = 2; i <= sqrt(num); i++)
if (num % i == 0)
return 0;
return 1;
}
bool isok(int num)
{
int ok = 0;
int s = 1;
if (num < 6)
return false;
for (int i = 2; i <= sqrt(num); i++)//将此数分解质因数
{
if (num % i == 0)
{
ok = 1;
if (isp(i))
s *= i;
if ((num / i != i) && isp(num / i))
s *= (num / i);
}
}
if (s == num)//s是累乘结果
return 1;
else
return 0;
}
int main()
{
int n;
cin >> n;
for (int i = 6; i <= n; i++)
if (isok(i))
printf("%d ", i);
return 0;
}
问题 L: 安装饮水机
- 这个题刚开始我想用二分...后来仔细一想大概不是,直接贪心就好,
- 贪心思想,每次安装饮水机都安装在当前观察员能到达的远的位置(向后),如果当前观察员能到达上一个饮水机,则这个观察员就不必安装饮水机,继续往后枚举
- 但这里有个问题,当一个观察员的覆盖范围在另一个观察员覆盖范围之内就会出问题
这时我想到要去重,把范围大的观察员全部踢掉,因为如果我们能满足一个小范围的观察员的饮水需求,那么能到达这个小范围观察员的其它所有大范围观察员都能被满足。想一想
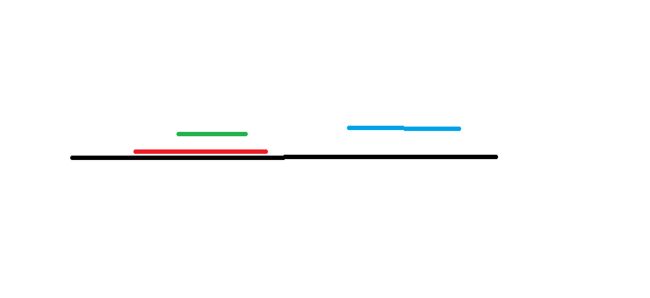
- 这里每个颜色各表示一个观察员的覆盖范围,如果我们能满足绿色观察员的饮水需求,也就是我们在绿色范围内建一个饮水机的话,红色和黑色我们还需要考虑嘛?
当然不用,因为他们两个一定能到达绿色那里,当然蓝色就不一定了。- 这个时候我们把饮水机尽量建在绿色最右边,继续枚举下一个观察员,如果下一个观察员的范围能与绿色相交,我们自然也不用考虑啊,如果不相交,那就在他的最右边安装饮水机就好了
- 关键步骤:排序,去重
#include
#include
#include
#include
#include
using namespace std;
int n;
int v[2000];
struct ss
{
int k;
int l;
int r;
} s[1005];
bool cmp(ss a, ss b)
{
if (a.r == b.r)
return a.l < b.l;
else
return a.r < b.r;
}
int main()
{
cin >> n;
for (int i = 0; i < n; i++)
{
int p;
cin >> s[i].k >> p; //k表示观察员的坐标,l是左边界,r是右边界
s[i].l = s[i].k - p;
s[i].r = s[i].k + p;
}
sort(s, s + n, cmp); //安装我的规则排序,先安装右边界,再安装左边界
for (int i = 0; i < n; i++)
{
for (int j = i + 1; j < n; j++)
{
if (s[j].l > s[i].l)
break;
if (s[j].r < s[i].r)
continue;
if (s[j].r >= s[i].r && s[j].l <= s[i].l)
v[j] = 1; //去重我们就标记一下就好了,到时候直接跳过就行
}
}
int now = s[0].r;
int ans = 1;
for (int i = 1; i < n; i++)
{
if (v[i])
continue;
if (s[i].l <= now) //如果当前观察员能到达上一个饮水机,那就不用安装新的饮水机
continue;
if (s[i].l > now) //如果当前观察员不能到达,那就安装饮水机
{
ans++;
now = s[i].r;
}
}
cout << ans;
return 0;
}
- 这个题数据真的水,不跳过大区间都能过...