前言
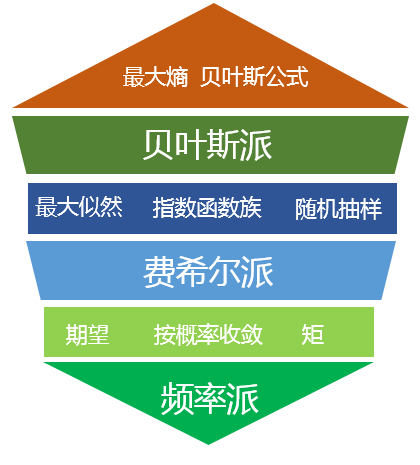
在“免费: 大赏新书CASI”里面斯坦福的优化大师Efron对统计的描述有一个三角形, 这个三角形的三个顶点分别是频率派(Frequentist), 费希尔派(Fisherian)和贝叶斯派(Bayesian)。 这个FFB就是我们要说的三层奥义! 要充分理解概率分布也要从这三层奥义出发。
什么是FFB三奥义?
什么是频率派?
频率派就是本着客观事实的思想, 从数学极限的角度出发, 建立概率思想。 这个过程很重要的支柱就是大数定理! 而早期最重要的一个大数定理就是伯努利大数定理,这是Jacob Bernoulli建立起来的(详细参考变分の美), 这也是按概率收敛的最早形式。
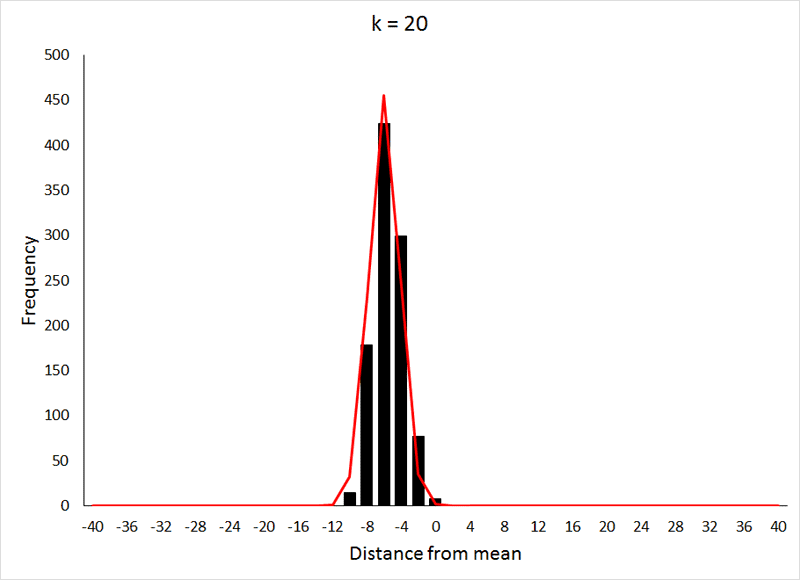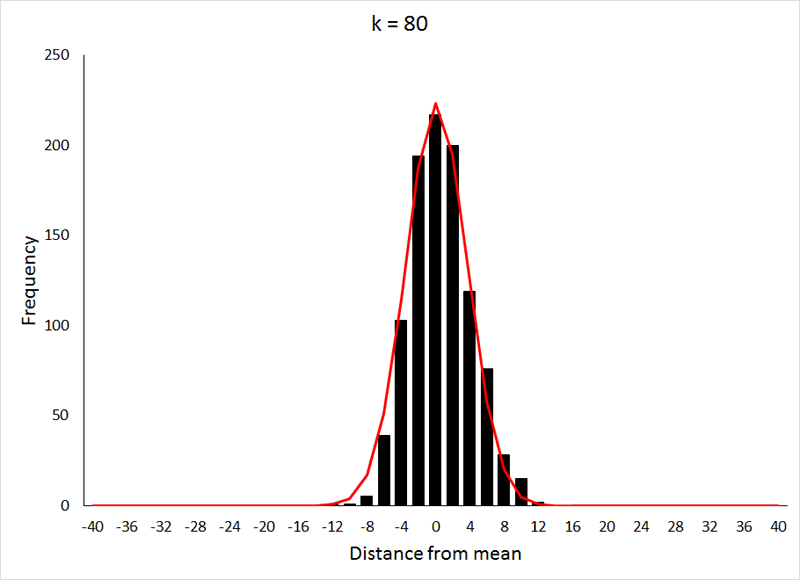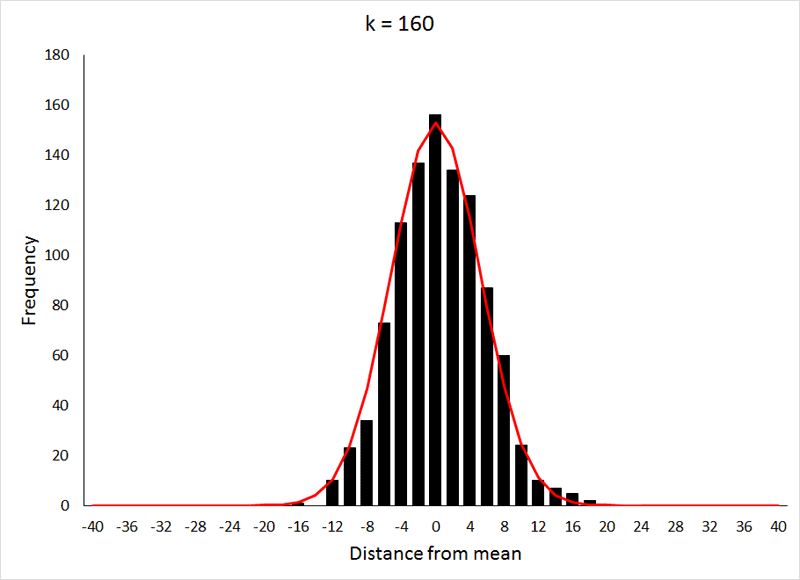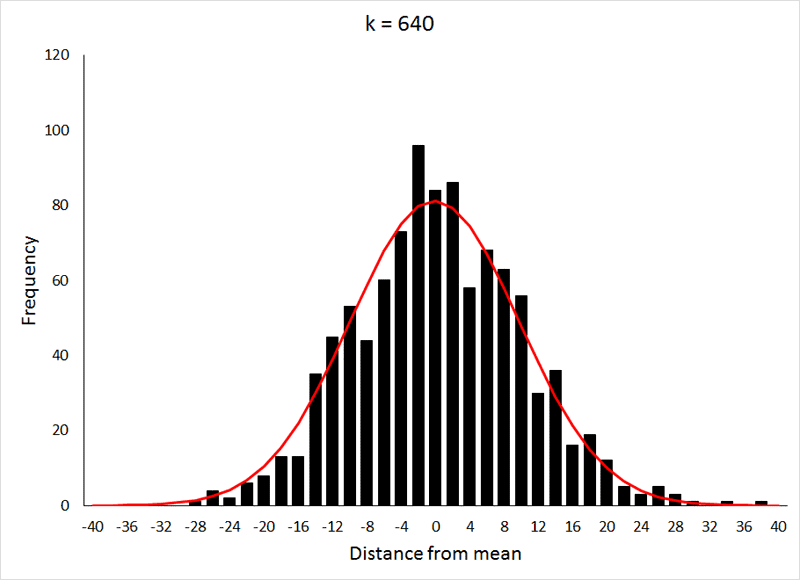
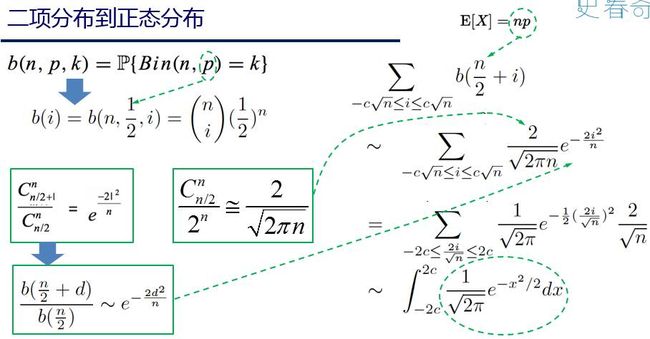
根据大数定理, 我们知道二项分布的极限情况就是正态分布。 关于正态分布可以参考RickJin的“正态分布的前世今生”。
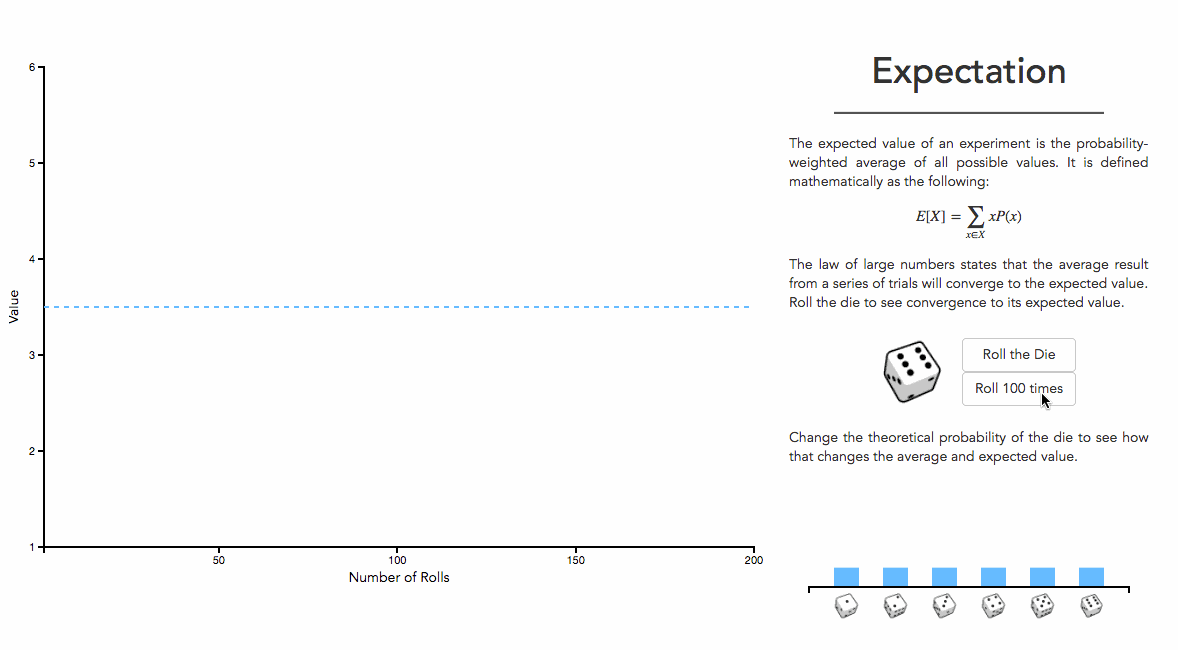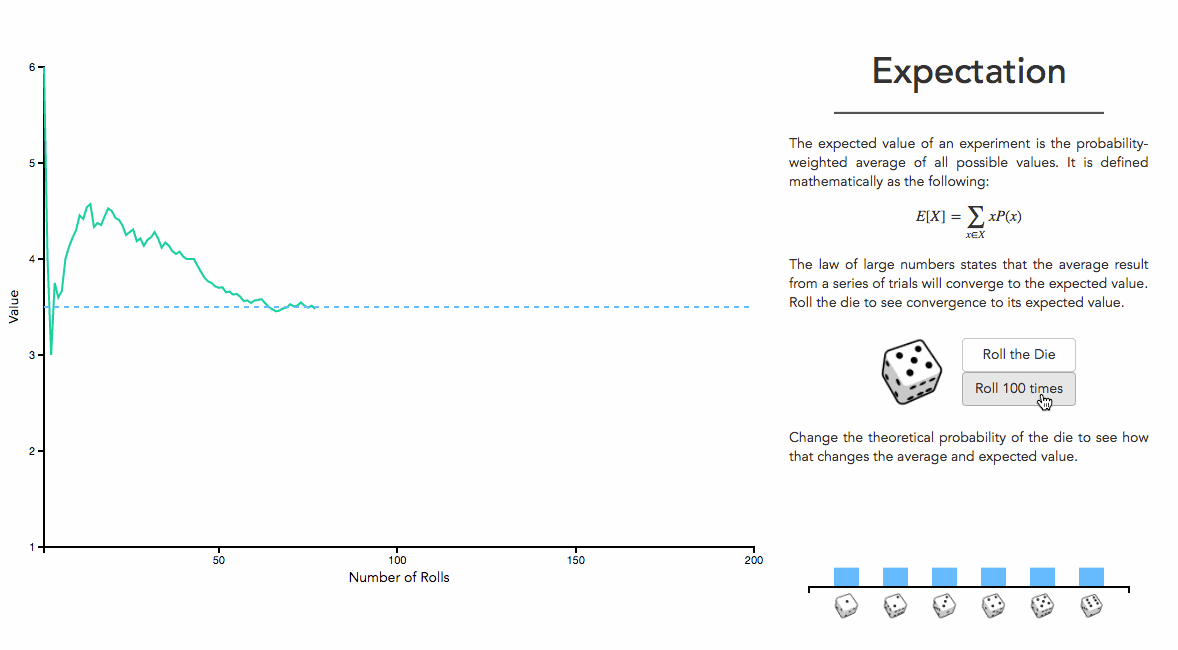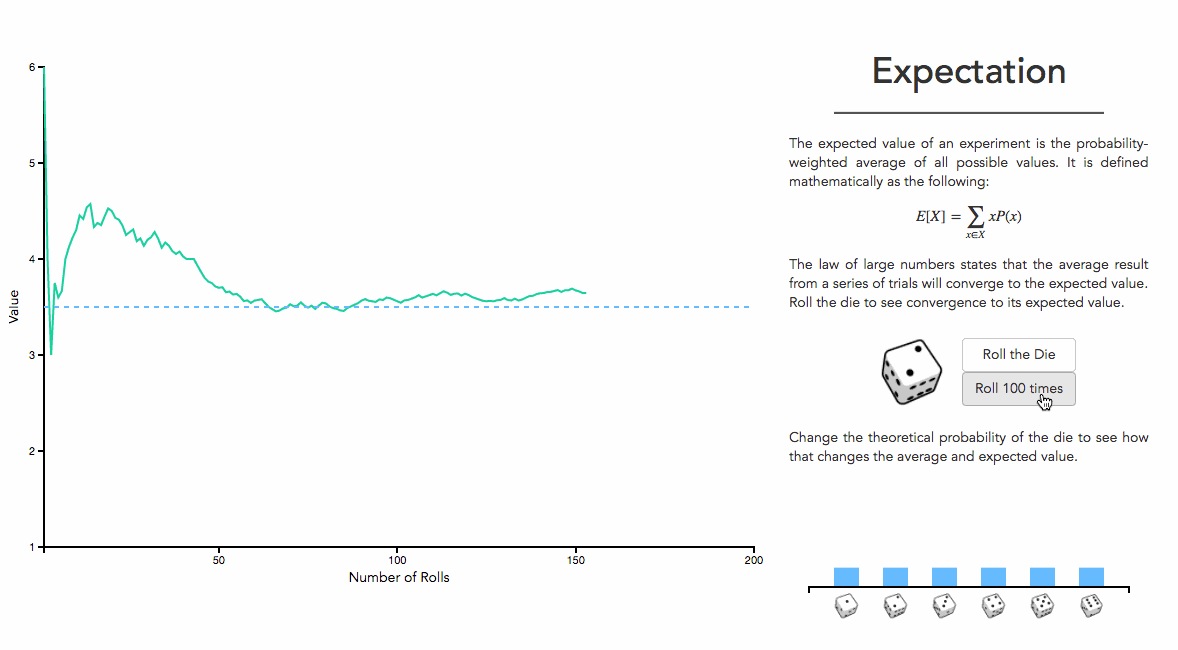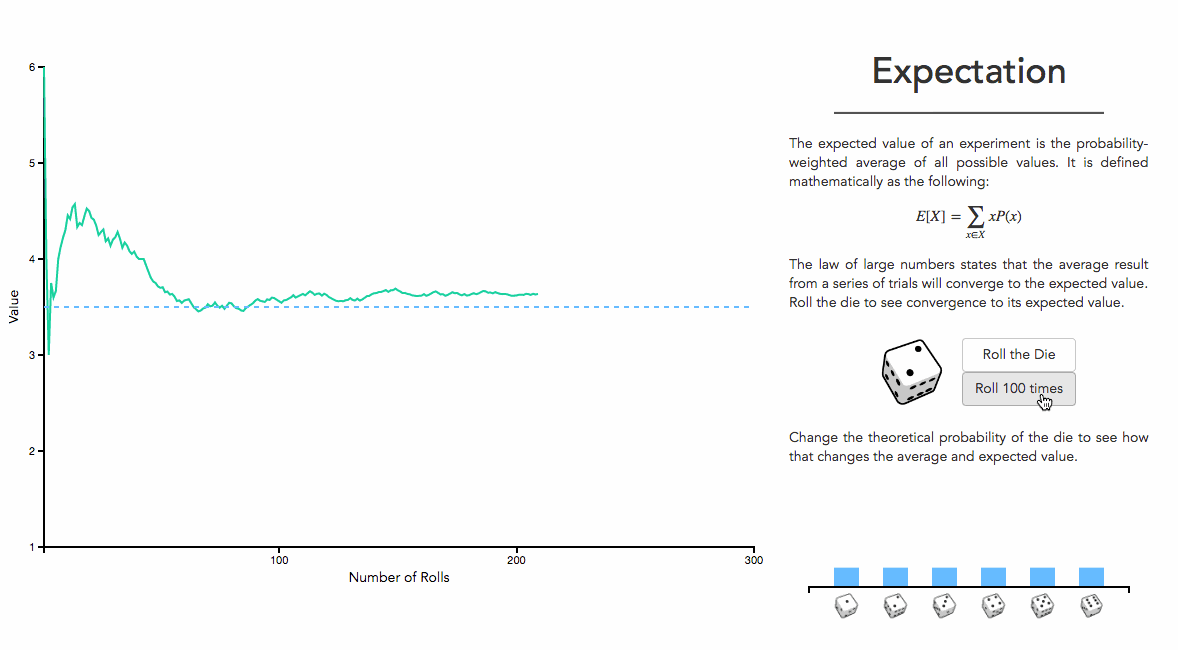
很直观的来说, 基于频率的情况下, 需要超级大数据量的实验。 好处也非常明显, 可以建立起来坚实的理论基础。 譬如, 数学期望的表示,就有一个数学收敛的过程!
简单说来, 频率派就是从海量数据事实出发,利用数据极限的思想建立起概率分布来。
什么是费希尔派?
费希尔派是指主要统计的思路。 什么是统计的思路,就是根据经验出发建立起来的合理解释。 所谓合理,就是最大似然的基本思想。 这个思想的集大成者就是Fisher 费希尔。
譬如, 高斯是基于经验推理的高高手(详细参考一步一步走向锥规划 - LS), 他根据天文数据处理一个最常用的经验是: 均值最优。 那么根据均值最优的经验假设下, 寻找误差满足的分布, 从而定义了正态分布。
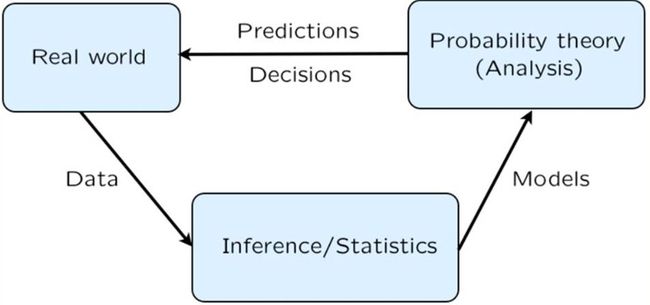
费希尔派和频率派的不同点有点类似统计和概率的不同。 我们知道, 统计的角度和概率的角度有很大的不同。概率的角度, 是根据大数定理,基于频率出发先计算出概率的分布, 然后再去研究。 而统计的角度,是直接根据经验假设, 然后去拟合数据分布, 再去研究。
那么费希尔学派最大的理论基础就是, 费希尔Fisher建立的最大似然拟合 和 充分统计量 的思想。 根据最大似然的思想, 首先我们需要根据经验来寻找一个最符合有限的数据的曲线。
那么,什么又是充分统计量的思想呢? 其实这也是奥卡姆剃刀原理在统计里面的一种具体化。 根据奥卡姆剃刀原理,那么找到的曲线要求尽可能的形式简单。
而费希尔定义了, 这种拟合曲线的表达式的简单形式应该是可以划分成两个部分, 一个部分只是和已知数据h(X)有关系。而另外一部分只和参数ϴ和数据上计算表达式T(X)为自变量的函数g(,)有关。 如果这个拟合曲线能进行这样的划分, 那么数据上的数据表达式T(X)就是已知数据的充分统计量了:
所以,最大似然估计告诉我们如何将曲线和数据进行拟合了。 而充分统计量告诉我们如何定义曲线表达式的形式了。 那么, 根据费希尔定义好的经验, 我们就可以从数据出发找到概率分布了。
简单来说, 费希尔派就是基于有限数据, 利用经验表示的思想, 建立概率分布的思想。 这个过程,明显的容忍了对事实数据的观测的大量减少!!!
什么是贝叶斯派?
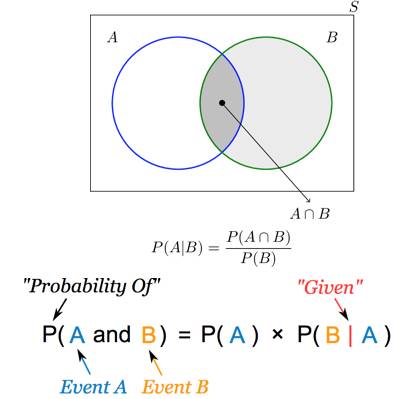
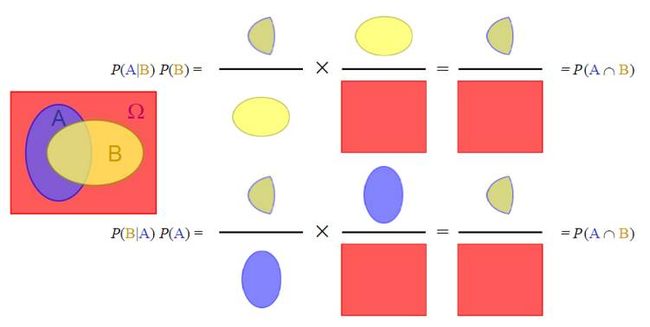
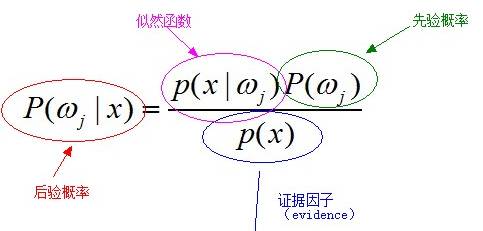
贝叶斯派主要是推理的思想。 而这个推理是建立在bayes定理的基础上的。
贝叶斯定理从集合论的角度告诉我们, 统一事实, 你可以从两个不同的角度去分阶段理解。
你可以站在A的角度去看B,也可以站在B的角度去看A。 他们看到的事实应该是一致的的。
那么, 根据费希尔里面提出的有限数据X加参数ϴ的思想, 就可以进行参数和数据的基础上进行推理了。
虽然贝叶斯派吸收了费希尔派关于有限观测和参数的思想, 但是缺摒弃了经验最优的思想。 而是选择了最大熵原理。
最大熵原理告诉我们, 在给定限制的情况下, 要均匀的充满整个限制空间的基本原理。
所以, 把已知数据看成是一种限制, 那么均匀的充满限制的最大熵情况就是贝叶斯派告诉我们的概率分布。 并且基于这个原理, 给出了费希尔派的关于最大似然估计的证明(参考 “最大似然估计的2种论证”)。
简而言之,贝叶斯派吸收了费希尔的有限观测的思想, 但是摒弃的经验, 选择了一个最大熵原理和贝叶斯推理来建立概率思想。
三奥义下的概率分布?
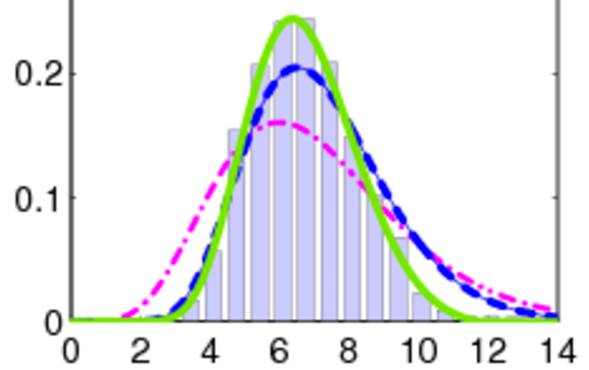
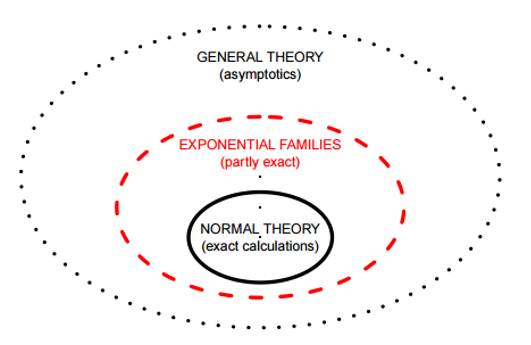
概率分布中, 最重要的是指数族分布。 而这个核心又是正态分布。
频率派下的概率分布
在这个派别下, 棣莫弗de Moivre利用自己的好朋友Stirling确定的Stirling公式, 加上从二项分布,对期望为中心求极限分布的思想, 得到了正态分布。更多细节参考“正态分布的前世今生” 。
有了这个伟大的基础, 再有各种分布进行观测量的变换, 极限的变换, 离散到连续的变换等等, 建立起来强大的概率分布体系。 细节就不展开了。
譬如, 伯努利分布 就是抛一个硬币,重复多次就是二项分布等价于抛多次硬币, 二项分布如果观测值修改为硬币正面出现的次数,就是泊松分布, 等等 。。。
费希尔派下的概率分布
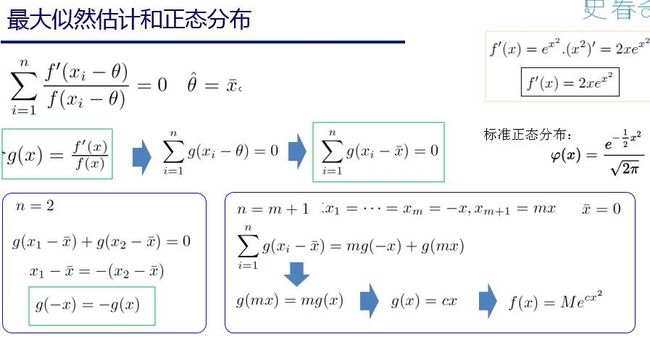
在这个派别下,由高斯基于均值最优的经验, 基于最大似然的思想找到误差分布, 也就是正态分布。 更多细节参考“正态分布的前世今生” 。
有了这个理论基础, 再基于费希尔的充分统计量, 给出各种统计量, 建立了指数族分布。
贝叶斯派下的概率分布
在这个派别下, 在Edwin Thompson Jaynes利用最大熵原理改写了费希尔派的经验思想。 就变得异常强大。 在最大熵的基础上(详细参考信息熵的由来),指数族分布不在是经验公式, 而是可以证明的一个表达式。
首先给出三个基础假设:有限数据假设, 概率分布假设, 和 统计量假设。
在这三个假设的基础上, 给定最大熵目标:
有了最大熵目标,就可以利用拉格朗日乘数法进行求解了(详细参考一挑三 FJ vs KKT):
这样, 我们就根据最大熵推出了指数族分布的形式了。 更为详细参考“66天写的逻辑回归” 引。
简而言之,频率派的极限收敛,费希尔派的经验拟合, 和贝叶斯派的最大熵推理, 都是概率分布的源泉。
小结:
概率统计的发展从频率派,费希尔派, 到贝叶斯派,要求的事实观测越来越少, 要求的经验也越来越少。 体现了概率的精华,以少测多, 见微知著的智慧!
相关话题:
最大似然估计的2种论证
信息熵的由来
“66天写的逻辑回归” 引
一步一步走向锥规划 - LS
一挑三 FJ vs KKT
变分の美
矩阵分解 (乘法篇)
矩阵分解 (加法篇)
收敛率概述 (Overview of Rates of Convergence)
迭代优化算法之直观概述 (SVRG)
参考:
正态分布的前世今生-rickjin-v1.2.pdf