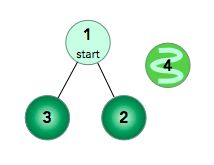
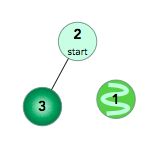
- [Swift]LeetCode943. 最短超级串 | Find the Shortest Superstring
黄小二哥
swift
★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★➤微信公众号:山青咏芝(shanqingyongzhi)➤博客园地址:山青咏芝(https://www.cnblogs.com/strengthen/)➤GitHub地址:https://github.com/strengthen/LeetCode➤原文地址:https://www.cnblogs.com/streng
- 生成式地图制图
Bwywb_3
深度学习机器学习深度学习生成对抗网络
生成式地图制图(GenerativeCartography)是一种利用生成式算法和人工智能技术自动创建地图的技术。它结合了传统的地理信息系统(GIS)技术与现代生成模型(如深度学习、GANs等),能够根据输入的数据自动生成符合需求的地图。这种方法在城市规划、虚拟环境设计、游戏开发等多个领域具有应用前景。主要特点:自动化生成:通过算法和模型,系统能够根据输入的地理或空间数据自动生成地图,而无需人工逐
- svg图片兼容性和用法优缺点
独行侠_ef93
svg图片的使用方法第一次来认认真真的研究了下svg图片,之前只是在网上见过,但都是一晃而过也没当回事,最近网站改版看到同事有用到svg格式的图片,想想自己干了几年的重构也没用过,这些细节的知识是应该好好研究研究了。暂时还没研究得完全透切,先记下目前为止所看到的吧不然又给忘了。svg可缩放矢量图形(ScalableVectorGraphics),顾名思义就是任意改变其大小也不会变形,是基于可扩展标
- tf.get_collection()
yalesaleng
此函数有两个参数,key和scope。Args:1.key:Thekeyforthecollection.Forexample,theGraphKeysclasscontainsmanystandardnamesforcollections.2.scope:(Optional.)Ifsupplied,theresultinglistisfilteredtoincludeonlyitemswhose
- Spark 组件 GraphX、Streaming
叶域
大数据sparkspark大数据分布式
Spark组件GraphX、Streaming一、SparkGraphX1.1GraphX的主要概念1.2GraphX的核心操作1.3示例代码1.4GraphX的应用场景二、SparkStreaming2.1SparkStreaming的主要概念2.2示例代码2.3SparkStreaming的集成2.4SparkStreaming的应用场景SparkGraphX用于处理图和图并行计算。Graph
- 1-1.Jetpack 之 Navigation 简单编码模板
我命由我12345
Android-Jetpack简化编程javajava-eeandroid-studioandroidstudio安卓androidjetpack
一、Navigation1、Navigation概述Navigation是Jetpack中的一个重要成员,它主要是结合导航图(NavigationGraph)来控制和简化Fragment之间的导航,即往哪里走,该怎么走2、Navigate引入在模块级build.gradle中引入相关依赖implementation'androidx.navigation:navigation-fragment:2
- Swift4.0: 利用图形上下文画基础图?
Dayu大鱼
步骤:开启图片上下文获取上下文配置上下文3.1填充颜色cgColor3.2填充尺寸从图形上下文中获取图片关闭上下文返回图片importFoundationimportUIKitextensionUIImage{///画一个白色背景的图片classfuncimageWithWhiteBackGroundColor()->UIImage{//开始图形上下文UIGraphicsBeginImageCon
- 主流行架构
rainbowcheng
架构架构
nexus,gitlab,svn,jenkins,sonar,docker,apollo,catteambition,axure,蓝湖,禅道,WCP;redis,kafka,es,zookeeper,dubbo,shardingjdbc,mysql,InfluxDB,Telegraf,Grafana,Nginx,xxl-job,Neo4j,NebulaGraph是一个高性能的,NOSQL图形数据库
- 深入学习-Gradle-自动化构建技术(五)Gradle-插件架构实现原理剖析-
2401_84002294
2024年程序员学习学习自动化架构
6、AndroidGradlePluginV3.0.0(2017年10月)7、AndroidGradlePluginV2.3.0(2017年2月)三、Gradle构建核心流程解析1、LoadSettings2、Configure3、TaskGraph4、RunTasks5、Finished四、关于Gradle中依赖实现的原理1、通过MethodMissing机制,间接地调用DefaultDepen
- Webpack 概念速通:从入门到掌握构建工具的精髓
tabzzz
前端webpack前端
Webpack基本概念这里我们先简单熟悉下Webpack的基本概念,我们在搭建项目的时候都会要用到的!这里我们分享的着重点是基本概念而不是具体配置项和使用方法依赖图(dependencygraph)模式(mode)入口(entry)输出(output)加载器(loader)插件(plugin)源映射(SourceMaps)开发服务器(devServer)依赖图(dependencygraph)依赖
- 【Leetcode】581. Shortest Unsorted Continuous Subarray
云端漫步_b5aa
Givenanintegerarray,youneedtofindonecontinuoussubarraythatifyouonlysortthissubarrayinascendingorder,thenthewholearraywillbesortedinascendingorder,too.Youneedtofindtheshortestsuchsubarrayandoutputitsle
- 概率图模型(PGM)综述
医学影像处理
概率图模型概率图模型综述
RefLink:http://www.sigvc.org/bbs/thread-728-1-1.htmlGraphicalModel的基本类型基本的GraphicalModel可以大致分为两个类别:贝叶斯网络(BayesianNetwork)和马尔可夫随机场(MarkovRandomField)。它们的主要区别在于采用不同类型的图来表达变量之间的关系:贝叶斯网络采用有向无环图(DirectedAc
- Webpack和Vite的区别
南辞w
前端面试篇webpack前端node.js
什么是webpack?webpack是一个用于现代JavaScript应用程序的静态模块打包工具。当webpack处理应用程序时,它会在内部从一个或多个入口点构建一个依赖图(dependencygraph),然后将你项目中所需的每一个模块组合成一个或多个bundles,它们均为静态资源,用于展示你的内容。Webpack的打包构建流程Webpack会遍历你应用程序中的所有文件,并启动一个开发服务器,
- 算法练习——迷宫问题(Java)bfs广搜
流萤点火
算法bfsjava
问题描述:小明置身于一个迷宫,请你帮小明找出从起点到终点的最短路程。小明只能向上下左右四个方向移动。输入输入包含多组测试数据。输入的第一行是一个整数T,表示有T组测试数据。每组输入的第一行是两个整数N和M(1que,intgx,intgy,intn,intm,char[][]arr){Qq=newQ();q.x=sx;q.y=sy;q.dept=0;que.add(q);//添加intfinish
- 数据结构OJ作业——队列
nnbs
数据结构数据结构poj队列
POJ3984:http://poj.org/problem?id=3984迷宫,输出最短路径,bfs#include#include#include#includeusingnamespacestd;intmaze[5][5];pairpath[5][5];queue>q;intdx[]={1,-1,0,0};intdy[]={0,0,1,-1};voidbfs(intx,inty){q.pus
- 【RKNN系列】常用函数:使用RGA加速画框
jcfszxc
RKNN系列Rockchiprknn-toolkit2c++RKNN
以下是针对convert_and_draw_rectangle函数的详细使用说明:convert_and_draw_rectangle函数功能在给定的图像数据上使用RGA(RockchipGraphicsAcceleration)绘制矩形框。语法IM_STATUSconvert_and_draw_rectangle(uint8_t*dst_data,intwidth,intheight,const
- 数据结构与算法——7-6 列出连通集 (25分)
吃完有点累
数据结构与算法队列算法数据结构DFSBFS
7-6列出连通集(25分)给定一个有N个顶点和E条边的无向图,请用DFS和BFS分别列出其所有的连通集。假设顶点从0到N−1编号。进行搜索时,假设我们总是从编号最小的顶点出发,按编号递增的顺序访问邻接点。输入格式:输入第1行给出2个整数N(0#includetypedefintVertexType;typedefintEdgeType;#defineMAXVEX100#defineINFINITY
- 7-6 列出连通集 (25 分)
胡小涛
DFSBFS
7-6列出连通集(25分)给定一个有N个顶点和E条边的无向图,请用DFS和BFS分别列出其所有的连通集。假设顶点从0到N−1编号。进行搜索时,假设我们总是从编号最小的顶点出发,按编号递增的顺序访问邻接点。输入格式:输入第1行给出2个整数N(0#includeusingnamespacestd;typedefstructGNode{intn;inte;intAdjMatrix[11][11];};s
- 7-7 六度空间
polebugzhuzhu
算法数据结构
输入样例:1091223344556677889910输出样例:1:70.00%2:80.00%3:90.00%4:100.00%5:100.00%6:100.00%7:100.00%8:90.00%9:80.00%10:70.00%分析:对每个点bfs前六层,为了使得d数组除了能表示距离,还能表示是否visted,所以d从1开始。用vectore[N];邻接表,对一个点的bfs=O(m),总时间
- arXiv综述论文“Graph Neural Networks: A Review of Methods and Applications”
硅谷秋水
自动驾驶
arXiv于2019年7月10日上载的GNN综述论文“GraphNeuralNetworks:AReviewofMethodsandApplications“。摘要:许多学习任务需要处理图数据,该图数据包含元素之间的丰富关系信息。建模物理系统、学习分子指纹、预测蛋白质界面以及对疾病进行分类都需要一个模型从图输入学习。在其他如文本和图像之类非结构数据学习的领域中,对提取的结构推理,例如句子的依存关系
- C# 图形图像技术(通过Graphics绘制图像)
萨达大
c#开发语言
文章目录创建Graphics对象画笔与画刷画笔画刷SolidBrush类HatchBrush类LinerGradientBrush类基本图形绘制矩形椭圆圆弧扇形创建Graphics对象privatevoidForm1_Load(objectsender,Eventargse){Graphicsghs=this.CreateGraphics();}画笔与画刷画笔构造函数publicPen(Color
- Python 对文件的加密和解密
Jinx Boy
python哈希算法开发语言
cryptography库中的Fernet模块提供了一种简单的方法来加密和解密数据。它使用对称加密算法,其中相同的密钥用于加密和解密数据。以下是用Fernet模块对文件进行的加密和解密。加密:importhashlibimportbase64fromcryptography.fernetimportFernetimportosdefstring_to_fernet_key(input_string
- 推荐:ASP.NET Core Web API 模板 —— 强大的启动项目!
戴洵珠Gerald
推荐:ASP.NETCoreWebAPI模板——强大的启动项目!aspnetcore-webapi-templateThisprojectisanWebAPIOpen-SourceBoilerplateTemplatethatincludesASP.NETCore5,WebAPIstandards,cleann-tierarchitecture,GraphQLservice,Redis,Mssql
- C# DrawString 水平及垂直居中
小黄人软件
C#c#
publicstaticBitmapgetPictureIMEI(stringtemplatePathName,stringimei){try{Bitmapbmp=newBitmap(templatePathName);Graphicsg=Graphics.FromImage(bmp);Fontf=newFont("Arial",12,FontStyle.Bold);RectangleFrect=
- 获取指定城市的路网数据(Python+Openstreetmap)
FORGIVEN_H
PYTHON入门python开发语言arcgis
在物流或者交通领域,经常需要获取某个地区或城市的路网数据,但是没有接触过这方面的人一开始都会有点摸不着头脑,刚好今天帮室友处理了一下这个问题,借助AI的力量解决了,浅做记录也方便大家使用。importosmnxasox#设置城市名称和国家代码city="Caofeidian,China"#下载路网数据graph=ox.graph_from_place(city,network_type='driv
- Android Graphics 显示系统 - VirtualDisplay的初印象 - 简单示例
向晚流年
android
“开始准备这篇文章时巴黎奥运会赛场上激战正酣,写完时奥运已落下帷幕,期间也看了许多精彩的赛事直播,拼搏与汗水书写的传奇无不激励着平凡岗位上的我们。每一枚奖牌的背后,都凝聚着运动员数不尽的汗水付出与坚持不懈,学习AndroidGraphics显示系统的知识,也需要我们长久的坚持、不断地探索实践。一点一滴地积累,一万小时天才定律,相信你终将赢得属于自己的金牌。”前言在许多场景中都会用到Android虚
- 图计算:基于SparkGrpahX计算聚类系数
妙龄少女郭德纲
Spark图算法Scala聚类数据挖掘机器学习
图计算:基于SparkGrpahX计算聚类系数文章目录图计算:基于SparkGrpahX计算聚类系数一、什么是聚类系数二、基于SparkGraphX的聚类系数代码实现总结一、什么是聚类系数聚类系数(ClusteringCoefficient)是图计算和网络分析中的一个重要概念,用于衡量网络中节点的局部聚集程度。它有助于理解网络中节点之间的紧密程度和网络的结构特性。这是一种用来衡量图中节点聚类程度的
- 牛客周赛 Round 13 解题报告 | 珂学家 | 乘法原理场 + BFS上组合 + 众数贪心
Buoluochuixue
java
题解|#简单计算器##includeintmain(){doublea,b;charoperate;scanf(&迈瑞医疗一面等了面试官十几分钟,更气人在后面上来自我介绍完了就让开始做题。。。题不算很难,做完了之后,讲了下思路,后面根据简历提问。一分钟简单介绍下实习做的东西,我说到一半经纬恒润Java开发一面时长:35min1.聊项目2.gc3.线程共享私有4.类加载过程5.I/O相关6.Spri
- 如何让echarts中title可以旋转以及在四周加上title
今晚吃什么呢?
echarts前端javascript
需要达到的效果图如下:需要实现这种的效果我们需要用到,graphic这个Api,具体实现:1.在graphic使用elements这个属性;2.设置title需要几个title你就设置几个;3.属性解释:type设置他的类型,可以是文字也可以是其他的。left、bottom、top等是设置他的位置使用center就是居中对齐style是设置他的样式益对象的形式出显;style.tex是设置名称,s
- 现代密码学2.2、2.3--由“一次一密”引出具有完美安全的密码方案共同缺点
WeidanJi
现代密码学概率论密码学数学
现代密码学2.2、2.3--由“一次一密/One-TimePad”引出具有完美安全的密码方案共同缺点One-TimePad密码方案定义正确性/correctness完美隐藏性/perfectlysecret具有完美隐藏性的密码方案的共同缺点特例缺点共同缺点博主正在学习INTRODUCTIONTOMODERNCRYPTOGRAPHY(SecondEdition)--JonathanKatz,Yehu
- SQL的各种连接查询
xieke90
UNION ALLUNION外连接内连接JOIN
一、内连接
概念:内连接就是使用比较运算符根据每个表共有的列的值匹配两个表中的行。
内连接(join 或者inner join )
SQL语法:
select * fron
- java编程思想--复用类
百合不是茶
java继承代理组合final类
复用类看着标题都不知道是什么,再加上java编程思想翻译的比价难懂,所以知道现在才看这本软件界的奇书
一:组合语法:就是将对象的引用放到新类中即可
代码:
package com.wj.reuse;
/**
*
* @author Administrator 组
- [开源与生态系统]国产CPU的生态系统
comsci
cpu
计算机要从娃娃抓起...而孩子最喜欢玩游戏....
要让国产CPU在国内市场形成自己的生态系统和产业链,国家和企业就不能够忘记游戏这个非常关键的环节....
投入一些资金和资源,人力和政策,让游
- JVM内存区域划分Eden Space、Survivor Space、Tenured Gen,Perm Gen解释
商人shang
jvm内存
jvm区域总体分两类,heap区和非heap区。heap区又分:Eden Space(伊甸园)、Survivor Space(幸存者区)、Tenured Gen(老年代-养老区)。 非heap区又分:Code Cache(代码缓存区)、Perm Gen(永久代)、Jvm Stack(java虚拟机栈)、Local Method Statck(本地方法栈)。
HotSpot虚拟机GC算法采用分代收
- 页面上调用 QQ
oloz
qq
<A href="tencent://message/?uin=707321921&Site=有事Q我&Menu=yes">
<img style="border:0px;" src=http://wpa.qq.com/pa?p=1:707321921:1></a>
- 一些问题
文强chu
问题
1.eclipse 导出 doc 出现“The Javadoc command does not exist.” javadoc command 选择 jdk/bin/javadoc.exe 2.tomcate 配置 web 项目 .....
SQL:3.mysql * 必须得放前面 否则 select&nbs
- 生活没有安全感
小桔子
生活孤独安全感
圈子好小,身边朋友没几个,交心的更是少之又少。在深圳,除了男朋友,没几个亲密的人。不知不觉男朋友成了唯一的依靠,毫不夸张的说,业余生活的全部。现在感情好,也很幸福的。但是说不准难免人心会变嘛,不发生什么大家都乐融融,发生什么很难处理。我想说如果不幸被分手(无论原因如何),生活难免变化很大,在深圳,我没交心的朋友。明
- php 基础语法
aichenglong
php 基本语法
1 .1 php变量必须以$开头
<?php
$a=” b”;
echo
?>
1 .2 php基本数据库类型 Integer float/double Boolean string
1 .3 复合数据类型 数组array和对象 object
1 .4 特殊数据类型 null 资源类型(resource) $co
- mybatis tools 配置详解
AILIKES
mybatis
MyBatis Generator中文文档
MyBatis Generator中文文档地址:
http://generator.sturgeon.mopaas.com/
该中文文档由于尽可能和原文内容一致,所以有些地方如果不熟悉,看中文版的文档的也会有一定的障碍,所以本章根据该中文文档以及实际应用,使用通俗的语言来讲解详细的配置。
本文使用Markdown进行编辑,但是博客显示效
- 继承与多态的探讨
百合不是茶
JAVA面向对象 继承 对象
继承 extends 多态
继承是面向对象最经常使用的特征之一:继承语法是通过继承发、基类的域和方法 //继承就是从现有的类中生成一个新的类,这个新类拥有现有类的所有extends是使用继承的关键字:
在A类中定义属性和方法;
class A{
//定义属性
int age;
//定义方法
public void go
- JS的undefined与null的实例
bijian1013
JavaScriptJavaScript
<form name="theform" id="theform">
</form>
<script language="javascript">
var a
alert(typeof(b)); //这里提示undefined
if(theform.datas
- TDD实践(一)
bijian1013
java敏捷TDD
一.TDD概述
TDD:测试驱动开发,它的基本思想就是在开发功能代码之前,先编写测试代码。也就是说在明确要开发某个功能后,首先思考如何对这个功能进行测试,并完成测试代码的编写,然后编写相关的代码满足这些测试用例。然后循环进行添加其他功能,直到完全部功能的开发。
- [Maven学习笔记十]Maven Profile与资源文件过滤器
bit1129
maven
什么是Maven Profile
Maven Profile的含义是针对编译打包环境和编译打包目的配置定制,可以在不同的环境上选择相应的配置,例如DB信息,可以根据是为开发环境编译打包,还是为生产环境编译打包,动态的选择正确的DB配置信息
Profile的激活机制
1.Profile可以手工激活,比如在Intellij Idea的Maven Project视图中可以选择一个P
- 【Hive八】Hive用户自定义生成表函数(UDTF)
bit1129
hive
1. 什么是UDTF
UDTF,是User Defined Table-Generating Functions,一眼看上去,貌似是用户自定义生成表函数,这个生成表不应该理解为生成了一个HQL Table, 貌似更应该理解为生成了类似关系表的二维行数据集
2. 如何实现UDTF
继承org.apache.hadoop.hive.ql.udf.generic
- tfs restful api 加auth 2.0认计
ronin47
目前思考如何给tfs的ngx-tfs api增加安全性。有如下两点:
一是基于客户端的ip设置。这个比较容易实现。
二是基于OAuth2.0认证,这个需要lua,实现起来相对于一来说,有些难度。
现在重点介绍第二种方法实现思路。
前言:我们使用Nginx的Lua中间件建立了OAuth2认证和授权层。如果你也有此打算,阅读下面的文档,实现自动化并获得收益。SeatGe
- jdk环境变量配置
byalias
javajdk
进行java开发,首先要安装jdk,安装了jdk后还要进行环境变量配置:
1、下载jdk(http://java.sun.com/javase/downloads/index.jsp),我下载的版本是:jdk-7u79-windows-x64.exe
2、安装jdk-7u79-windows-x64.exe
3、配置环境变量:右击"计算机"-->&quo
- 《代码大全》表驱动法-Table Driven Approach-2
bylijinnan
java
package com.ljn.base;
import java.io.BufferedReader;
import java.io.FileInputStream;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Collections;
import java.uti
- SQL 数值四舍五入 小数点后保留2位
chicony
四舍五入
1.round() 函数是四舍五入用,第一个参数是我们要被操作的数据,第二个参数是设置我们四舍五入之后小数点后显示几位。
2.numeric 函数的2个参数,第一个表示数据长度,第二个参数表示小数点后位数。
例如:
select cast(round(12.5,2) as numeric(5,2))
- c++运算符重载
CrazyMizzz
C++
一、加+,减-,乘*,除/ 的运算符重载
Rational operator*(const Rational &x) const{
return Rational(x.a * this->a);
}
在这里只写乘法的,加减除的写法类似
二、<<输出,>>输入的运算符重载
&nb
- hive DDL语法汇总
daizj
hive修改列DDL修改表
hive DDL语法汇总
1、对表重命名
hive> ALTER TABLE table_name RENAME TO new_table_name;
2、修改表备注
hive> ALTER TABLE table_name SET TBLPROPERTIES ('comment' = new_comm
- jbox使用说明
dcj3sjt126com
Web
参考网址:http://www.kudystudio.com/jbox/jbox-demo.html jBox v2.3 beta [
点击下载]
技术交流QQGroup:172543951 100521167
[2011-11-11] jBox v2.3 正式版
- [调整&修复] IE6下有iframe或页面有active、applet控件
- UISegmentedControl 开发笔记
dcj3sjt126com
// typedef NS_ENUM(NSInteger, UISegmentedControlStyle) {
// UISegmentedControlStylePlain, // large plain
&
- Slick生成表映射文件
ekian
scala
Scala添加SLICK进行数据库操作,需在sbt文件上添加slick-codegen包
"com.typesafe.slick" %% "slick-codegen" % slickVersion
因为我是连接SQL Server数据库,还需添加slick-extensions,jtds包
"com.typesa
- ES-TEST
gengzg
test
package com.MarkNum;
import java.io.IOException;
import java.util.Date;
import java.util.HashMap;
import java.util.Map;
import javax.servlet.ServletException;
import javax.servlet.annotation
- 为何外键不再推荐使用
hugh.wang
mysqlDB
表的关联,是一种逻辑关系,并不需要进行物理上的“硬关联”,而且你所期望的关联,其实只是其数据上存在一定的联系而已,而这种联系实际上是在设计之初就定义好的固有逻辑。
在业务代码中实现的时候,只要按照设计之初的这种固有关联逻辑来处理数据即可,并不需要在数据库层面进行“硬关联”,因为在数据库层面通过使用外键的方式进行“硬关联”,会带来很多额外的资源消耗来进行一致性和完整性校验,即使很多时候我们并不
- 领域驱动设计
julyflame
VODAO设计模式DTOpo
概念:
VO(View Object):视图对象,用于展示层,它的作用是把某个指定页面(或组件)的所有数据封装起来。
DTO(Data Transfer Object):数据传输对象,这个概念来源于J2EE的设计模式,原来的目的是为了EJB的分布式应用提供粗粒度的数据实体,以减少分布式调用的次数,从而提高分布式调用的性能和降低网络负载,但在这里,我泛指用于展示层与服务层之间的数据传输对
- 单例设计模式
hm4123660
javaSingleton单例设计模式懒汉式饿汉式
单例模式是一种常用的软件设计模式。在它的核心结构中只包含一个被称为单例类的特殊类。通过单例模式可以保证系统中一个类只有一个实例而且该实例易于外界访问,从而方便对实例个数的控制并节约系统源。如果希望在系统中某个类的对象只能存在一个,单例模式是最好的解决方案。
&nb
- logback
zhb8015
loglogback
一、logback的介绍
Logback是由log4j创始人设计的又一个开源日志组件。logback当前分成三个模块:logback-core,logback- classic和logback-access。logback-core是其它两个模块的基础模块。logback-classic是log4j的一个 改良版本。此外logback-class
- 整合Kafka到Spark Streaming——代码示例和挑战
Stark_Summer
sparkstormzookeeperPARALLELISMprocessing
作者Michael G. Noll是瑞士的一位工程师和研究员,效力于Verisign,是Verisign实验室的大规模数据分析基础设施(基础Hadoop)的技术主管。本文,Michael详细的演示了如何将Kafka整合到Spark Streaming中。 期间, Michael还提到了将Kafka整合到 Spark Streaming中的一些现状,非常值得阅读,虽然有一些信息在Spark 1.2版
- spring-master-slave-commondao
王新春
DAOspringdataSourceslavemaster
互联网的web项目,都有个特点:请求的并发量高,其中请求最耗时的db操作,又是系统优化的重中之重。
为此,往往搭建 db的 一主多从库的 数据库架构。作为web的DAO层,要保证针对主库进行写操作,对多个从库进行读操作。当然在一些请求中,为了避免主从复制的延迟导致的数据不一致性,部分的读操作也要到主库上。(这种需求一般通过业务垂直分开,比如下单业务的代码所部署的机器,读去应该也要从主库读取数