LeetCode 1091. Shortest Path in Binary Matrix

原题链接在这里：https://leetcode.com/problems/shortest-path-in-binary-matrix/

题目：

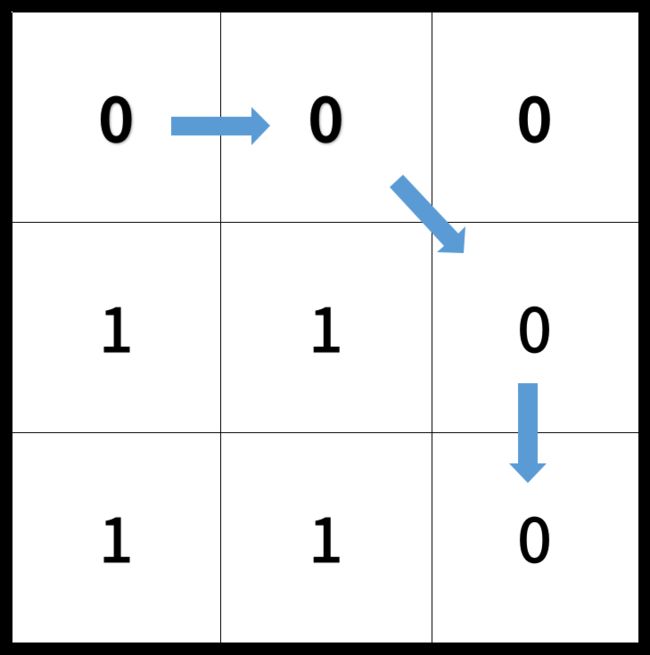
In an N by N square grid, each cell is either empty (0) or blocked (1).

A clear path from top-left to bottom-right has length k if and only if it is composed of cells C_1, C_2, ..., C_k such that:

• Adjacent cells C_i and C_{i+1} are connected 8-directionally (ie., they are different and share an edge or corner)
• C_1 is at location (0, 0) (ie. has value grid[0][0])
• C_k is at location (N-1, N-1) (ie. has value grid[N-1][N-1])
• If C_i is located at (r, c), then grid[r][c] is empty (ie. grid[r][c] == 0).

Return the length of the shortest such clear path from top-left to bottom-right.  If such a path does not exist, return -1.

Example 1:

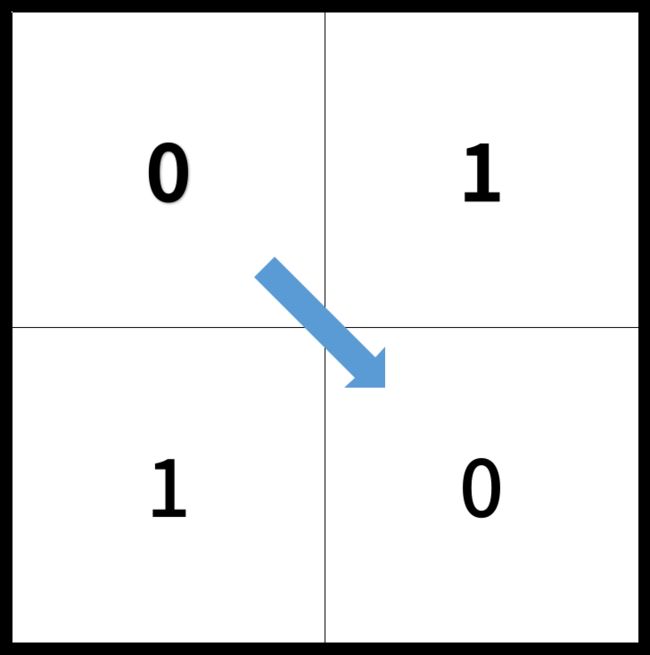
Input: [[0,1],[1,0]]


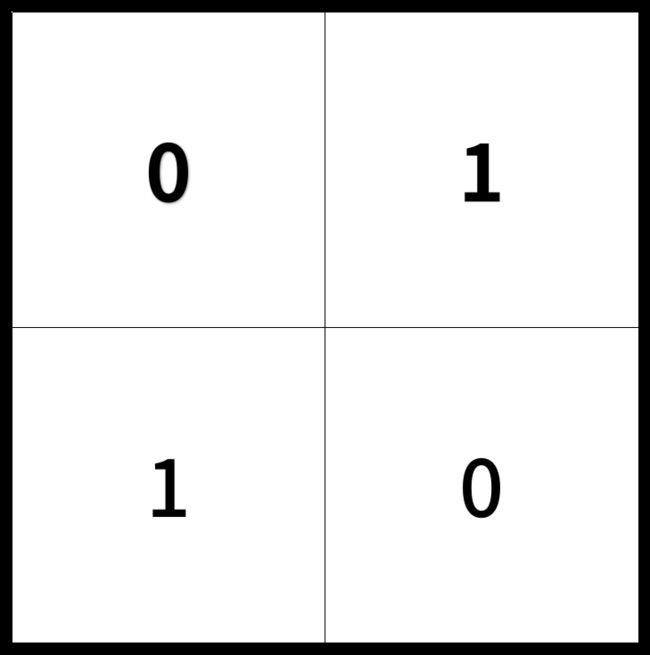Output: 2

Example 2:

Input: [[0,0,0],[1,1,0],[1,1,0]]


Output: 4

Note:

1. 1 <= grid.length == grid[0].length <= 100
2. grid[r][c] is 0 or 1

题解：

When doing BFS, for each level, mark the current size. 

When polling current size node, pop up to next level.

If current polled node is bottom right node, return level.

Otherwise, for its 8 surrounding node, check if it is not visited nor block, add it to the queue.

Time Complexity: O(m*n). m = grid.length. n = grid[0].length.

Space: O(m*n).

AC Java: 

 1 class Solution {
 2     public int shortestPathBinaryMatrix(int[][] grid) {
 3         if(grid == null || grid.length == 0 || grid[0].length == 0){
 4             return -1;
 5         }
 6         
 7         int m = grid.length;
 8         int n = grid[0].length;
 9         if(grid[0][0] == 1 || grid[m-1][n-1] == 1){
10             return -1;
11         }
12         
13         LinkedList<int []> que = new LinkedList<>();
14         boolean [][] visited = new boolean[m][n];
15         visited[0][0] = true;
16         que.add(new int[]{0, 0});
17         
18         int level = 1;
19         while(!que.isEmpty()){
20             int size = que.size();
21             while(size-->0){
22                 int [] cur = que.poll();
23                 if(cur[0] == m-1 && cur[1] == n-1){
24                     return level;
25                 }
26                 
27                 for(int i = -1; i<=1; i++){
28                     for(int j = -1; j<=1; j++){
29                         int x = cur[0]+i;
30                         int y = cur[1]+j;
31                         if(x<0 || x>=m || y<0 || y>=n || visited[x][y] || grid[x][y]==1){
32                             continue;
33                         }
34 
35                         visited[x][y] = true;
36                         que.add(new int[]{x, y});
37                     }
38                 }
39             }
40             
41             level++;
42         }
43         
44         return -1;
45     }
46 }