cvr 预估中的转化延迟反馈问题概述
先安利两篇比较有代表性的文章：
Modeling Delayed Feedback in Display Advertising 这篇主要思路是将延迟反馈问题的延迟建模成一个指数分布，然后和cvr一起进行学习。感觉应该算是首次在cvr领域对延迟反馈建模（或者建模比较好的）的论文了，非常推荐一看。A Nonparametric Delayed Feedback Model for Conversion Rate Prediction这篇更进一步，认为延迟的反馈分布可能和广告/用户/上下文都有关系，因此对延迟反馈的时间建模成一个可以学习的模型，和第一篇一样的方式与cvr进行联合建模。
转化率对计算广告的重要性是众所周知的，而o系广告计费方式更是对转化率预估的准确性提出了新的要求。相对于cpc计费方式，ocpc，ocpm，ocpa等方式因为更加注重“转化”，因此更受广告主的欢迎，未来也将是计算广告行业的主流实现形式。
而o系的计费方式中一个重要的公式就是ecpm的计算：ecpm = bid * pctr * pcvr。将pctr和pcvr分开计算有两点好处：不需要join长期的转化从而减轻pipeline的负载（因为最多只需要join点击的数据）；对转化少或者没有转化的数据预估会更准确，因为这时候pctr也能提供一部分信息。
评估广告投放效果的重要指标：转化率(conversion rate) —– 在广告网站上采取行动的人占总浏览人数的比例。使用机器学习预估 conversion rate，从而预估收益。
然而与点击行为可能在用户浏览后的很短时间内就发生并被广告系统收集不同，广告后续所产生的转化conversion很可能延时发生（更可能是通过不同的方式延迟上传的，如需要广告主回传的深度转化行为），比如看过一个商品广告，当时有些心动但并没有马上去买，过了几天按捺不住又去购买（Delayed Feedback），给建模带来困难。转化延迟的时间视具体平台和环境而异，有的可能有上月的延迟。
广告不是一个静态过程，当心的计划加入系统后，以历史数据建立的旧的模型在这些新的计划上的表现可能不好，因此保持模型的更新对于广告保持性能至关重要。因此解决转化延迟的问题也成为提高广告系统性能的一个有效方式。
转化行为反馈时间上的延迟会对模型的训练产生负向的影响，一个简单的做法可能是通过一个预先设定好的时间窗口来进行转化归因，使用经过了时间窗口并进行了归因后的数据来进行转化率模型的更新。但是这对时间窗口的选择带来了挑战，并且可能因为单一时间窗口带来调试上的不灵活：
- 如果时间窗口太短，一些样本将被错误的标记成负样本，但是未来将完成转化，从而学习到了错误的标签；
- 如果时间窗口过长的话，训练集的样本就可能向匹配时间窗口一样陈旧，因此可能有产生一个过时的模型的风险；过时的模型显然不适合快速变化的广告候选以及用户行为模式的变动
一些其他的方法来区分正样本和未标记样本的方法已经被研究过了，但是这些方法依赖于假设：标记为正的样本是从正样本类别中随机产生的，也就是说丢失标签为正的样本概率为常数。这对于刚刚发生点击行为的样本来说，假设可能不成立，而且对于点击发生后的不同时段，转化完成的概率也应当是不同的。
第一篇论文 Modeling Delayed Feedback in Display Advertising，提出的解决方式不包含固定的匹配窗口：当产生训练集的时候，对一个点击后的样本，当跟着一个转化的时候将被标记成正样本，否则将被标记成 unlabeled（这不能直接标记为负样本，因为接下来也可能产生转化）。
这篇论文提出了一个模型用来预估是否转化，另一个模型来捕获点击到转化的期望延迟时间的解决方案。这一模型和存活时间分析中使用的模型有很大相关性。类似的，对转化问题来说，一些延迟是censored（经过审查的），当在训练时候转化还没发生，而后续如果有转化的话，转化的延迟至少是从点击开始的时间。
这一建模以及问题的性质与survival time analysis的问题很相似，在未观测到最终结果的时候，从观测点开始到最终结果之间的期望时间至少是观测所经过的时间。但是和survival time analysis 中一个病人最后一定会死不一样，用户最后可能并不能发生转化。这就是需要两个模型的原因：一个用来预测用户是否会发生转化，另一个用来预测用户发生转化的情况下的延迟时间。两个模型同时训练（jointly）。事实上也不能将两个模型分开：当一个转化没发生时候，是将来会转化还是将不会转化是模糊不清的。这两个模型同时准确预估两个输出的概率，通过两个模型来建模转化与转化需要的期望时间。
根据以上的描述，论文中的建模主要包含以下几个变量：
下面附上第二篇论文中的变量说明，其基本变量和第一篇中的变量定义基本一致，增加的是部分模型参数，这个和其升级点有关，后续会说明。
由前面的分析知道：
- 当Y=1（已经发生了转化）的时候，C=1（用户最终发生了转化）；
- 当Y=0（转化还没发生）的时候，或者C=0（用户最终不会发生转化），或者E
该论文中的推导的仅有的独立假设是：（C, D）组合在给定X的情况下是独立于E的。 Pr(C,D∣X,E)=Pr(C,D∣X)。这一独立假设成立的原因是E点击后经过的时间只会影响Y。
观测到的变量，或者说下面用到的训练数据的形式是：
- 当y=0时候，(x, y, e)；
- 当y=1时候，(x, y, e, d)
插一个对survival analysis的说明（摘自第二篇）：
给定一随机变量T>0表示一个事件发生的时间，定义f(t)为T的概率密度，F(t)是累积分布函数（对f在0到t上的积分），事件直到事件t还没发生的概率由survival function给出：s(t) = 1 - F(t)，那么事件还没发生的比率由一个叫hazard function的h(t)给出，其关系：h(t) = f(t) / s(t)。由这个定义，survival function可以由h(t)推导出：s(t) = exp(- \int_0^t {h(x)} dx) 。
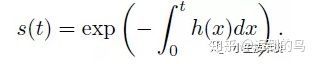
回到第一篇论文，论文提出的解决方法是两个模型同时训练的方式：
- 转化率模型采用一个标准的逻辑回归（目测也可以用别的方式）
- 预估转化延迟采用的是指数分布形式，文中提到其他的分布也可以，但是指数分布是一个常用且有效的拟合经验延迟分布的分布
逻辑回归和指数分布的形式：
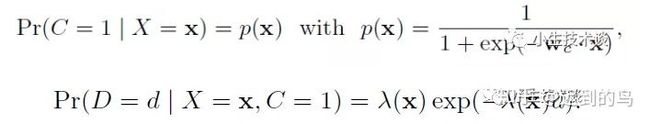
其中需要 λ(x)>0，因此文中设置 λ(x)=exp(w x) 是特征的一个指数形式，然后用参数w去拟合。
总结起来就是：
当然，延迟的分布拟合在实际应用中不一定被抛弃，还有别的用处，这里先不细说，只描述基本的join训练的思路。
模型建立好后，就需要讨论优化方式了，文中提供了先EM和直接梯度下降两种方式，具体其实也用了梯度下降的方式。现在深度学习工具包都是自动求梯度了，因此考虑到工程实现等方便性，实际应用肯定首选gd类优化方法。具体推导摘录如下（实际可能实现时候是使用tensorflow等，并不需要手推，这里也没再细看了）：
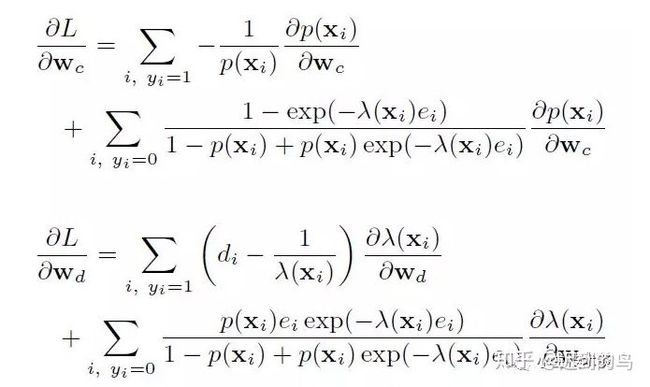
感觉第二篇论文的思路也是沿着第一篇论文，将是否转化和期望的转化时间进行分开为两个模型，并同时进行优化训练来建模的了。
第二篇论文的主要改进点是针对如下的考虑的：实际中，并不能保证延迟时间是服从指数分布的，表示延迟的最佳分布取决于数据。而且每个广告，不同上下文，不同的用户的延迟时间的期望分布的形态也应该是不一样的，因此第二篇将期望延迟时间的表示形式进行了模型化，感觉向着“神经网络化”更近了一步，建模的期望大概是可以通过参数的形式拟合不同数据以及业务，不同广告等的不同的期望分布形态。因此感觉和神经网络的“万能近似”定理的期望差不多了。
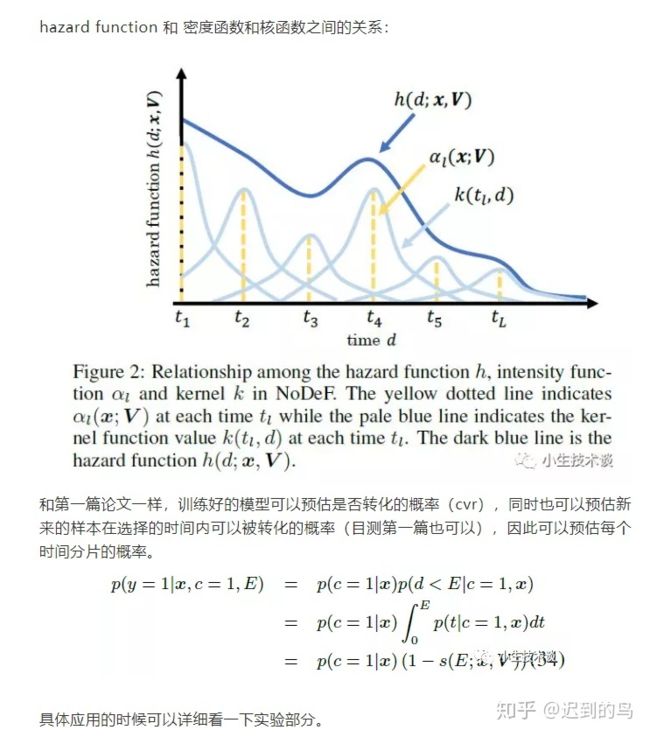
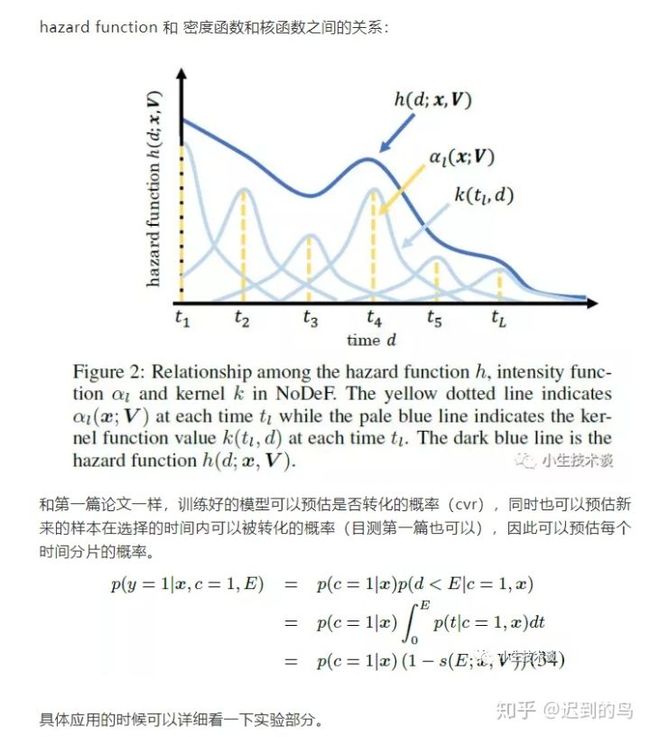
第二篇中将时间轴分成L份，建立L个虚拟的时间片，然后用到了上文提到的hazard function并且应用了一部分的KDE的思想，并且引入了核函数对期望的延迟时间进行建模：
|
|
具体后续的推导思路和第一篇感觉很相似，这里不再赘述了，其中显示的根据Y的值将集合分成两部分的方式值得注意一下，另外前面选的核函数是可积分成显式的表达式的，因此对推导也有一定的简化。后续优化方式用的是EM，感觉也可以用梯度下降直接优化。
总结：
两篇论文都是使用两个模型（cvr和转化期望时间）来进行的，因此思路上都可以借鉴。实际预估转化的时候，可以将转化的期望时间同时建模来试一下效果。
另外感觉multitask或者类似的模型在特定场合还是挺有用的，其他如pctr和pcvr同时训练的如ESMM等，算是解决问题的一个好思路吧。
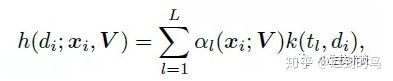
广告点击延时反馈建模
论文Modeling Delayed Feedback in Display Advertising阅读笔记
Abstract
评估广告投放效果的重要指标：转化率(conversion rate) —– 在广告网站上采取行动的人占总浏览人数的比例。使用机器学习预估 conversion rate，从而预估收益。
然而conversion很可能延时发生，比如看过一个商品广告，当时有些心动但并没有马上去买，过了几天按捺不住又去购买（Delayed Feedback），给建模带来困难。
这篇文章提出概率模型，对未采取行动的客户进行判别：可能会买or不可能会买
Introduction
广告计费模式：参考学习: 网络广告中，CPC、CPA、CPM 的定义各是怎样的？
这篇文章集中在CPA(cost per action)模式，更确切的说，是post-click conversion（点击后转化，转化被归因到之前的点击）。只有产生了预先商定的行动才付费。支持CPA模式的平台，就需要将广告标价，转化为eCPM(期望CPM），取决于conversion rate。
转化的延迟反馈特性导致构件训练集，设置匹配窗口长度的困难：过短则漏掉部分conversion；过长则导致模型停滞。
本文生成训练集时，将样本标记为positive和unlabeled，需要从正例和未标记数据中进行学习，但都假定标记正例从正类中随机选择，标签缺失的概率恒定。但与本文所讨论的情形不同：点击刚发生时，标签最易缺失。
本文引入模型II捕捉点击和转化之间的期望延迟，这有点类似于survival time analysis(生存时间分析，指治疗开始和患者死亡之间的时间)。有一些时间是截断（conversion一直没有发生）的， 这表明延迟（或者生存）时间至少是那个截断时间。
然而病人终有一死，而客户却未必转化。这就需要两个模型：一个预测是否转化；另一个预测相应的延迟时间。这两个模型共同训练，共同分配结果。
数据来源：Criteo流量日志；营利模式：收益（CPC/CPA，广告商）- 成本（CPM，出版商）
Conversions
Post-Click Attribution
post-view attribution: 将转化归因于之前的一次或几次浏览
post-click attribution: 将转化归因于被点击的广告
本文转化时间窗口长度固定为：30天
匹配除了时间窗要求，还要有相同的用户id和广告商。在多次点击导致一次转化时，按照行业标准归因于最后一次点击。若有多次转化匹配一次点击，则只保留第一个。也就是说，本文不考虑，单次点击导致多次转化的情形。
Conversion Rate Prediction
eCPM=CPA×Pr(conversion,click)eCPM=CPA×Pr(conversion,click)
=CPA×Pr(click)×Pr(conversion|click) =CPA×Pr(click)×Pr(conversion|click)
条件概率分解能降低数据负载，并且在没有conversion时仍能提供一定的click信息。建模Pr(click)需要可扩展的模型：单一平台每日广告投放量可达数十亿，而点击反馈是即时的；建模Pr(conversion | click)规模较小，但有反馈延迟。
Analysis of the Conversion Delay
New Campaigns
广告展示的各个因素都在持续变化，当新的活动被加入系统时，原来训练好的模型效能将会降低：Keep the model fresh！
在图2中，新活动的比例持续增长，这预示着30天的长时间窗模型将受到影响。
Model
XX：特征集
Y∈{0,1}Y∈{0,1}：转化是否已经发生
C∈{0,1}C∈{0,1}：用户是否终会转化
DD：点击和转化之间的延迟
EE：点击后已经流逝的时间
Y=0⟺C=0 or E
独立性假设：Pr(C,D|X,E)=Pr(C,D|X)Pr(C,D|X,E)=Pr(C,D|X)
也就是说，在这个模型中，不根据已经过了多久来判断转化最终是否发生和最终延迟时间。
给定数据集：(xi,yi,ei)(xi,yi,ei)，如果yi=1yi=1，还有相应的didi值。
用两个参数模型拟合数据：Pr(C|X),Pr(D|X,C=1)Pr(C|X),Pr(D|X,C=1)
训练好以后，前者被用来预测转换概率，后者被抛弃
这两个模型都是广义线性模型：前者是标准的逻辑回归：
Pr(C=1|X=x)=p(x),p(x)=11+exp(−wc⋅x)Pr(C=1|X=x)=p(x),p(x)=11+exp(−wc⋅x)
后者是延迟的指数分布：
Pr(D=d|X=x,C=1)=λ(x)exp(−λ(x)d)Pr(D=d|X=x,C=1)=λ(x)exp(−λ(x)d)
其中，为了保证λ(x)>0λ(x)>0，令λ(x)=exp(wd⋅x)λ(x)=exp(wd⋅x)
则该模型的参数就是wc,wdwc,wd
Pr(Y=1,D=di|X=xi,E=ei)Pr(Y=1,D=di|X=xi,E=ei)
=Pr(C=1,D=di|X=xi,E=ei)=Pr(C=1,D=di|X=xi,E=ei)
=Pr(C=1,D=di|X=xi)=Pr(C=1,D=di|X=xi)
=Pr(D=di|X=xi,C=1)Pr(C=1|X=xi)=Pr(D=di|X=xi,C=1)Pr(C=1|X=xi)
=λ(xi)exp(−λ(xi)di)p(xi)=λ(xi)exp(−λ(xi)di)p(xi)
Pr(Y=0|X=xi,E=ei)Pr(Y=0|X=xi,E=ei)
=Pr(Y=0|C=0,X=xi,E=ei)Pr(C=0|X=xi)=Pr(Y=0|C=0,X=xi,E=ei)Pr(C=0|X=xi)
+Pr(Y=0|C=1,X=xi,E=ei)Pr(C=1|X=xi)+Pr(Y=0|C=1,X=xi,E=ei)Pr(C=1|X=xi)
=1−p(xi)+p(xi)exp(−λ(xi)ei)=1−p(xi)+p(xi)exp(−λ(xi)ei)
⇑⇑
Pr(Y=0|C=1,X=xi,E=ei)=Pr(D>E|C=1,X=xi,E=ei)Pr(Y=0|C=1,X=xi,E=ei)=Pr(D>E|C=1,X=xi,E=ei)
=∫∞eiλ(x)exp(−λ(x)t)dt=exp(−λ(x)ei)=∫ei∞λ(x)exp(−λ(x)t)dt=exp(−λ(x)ei)
Optimization
Expectation-Maximization
EM算法学习参考:简单易学的机器学习算法——EM算法
把CC看作隐藏变量
Joint Optimization
Loss Function:
argminwc,wdL(wc,wd)+μ2(||wc||22+||wd||22)argminwc,wdL(wc,wd)+μ2(||wc||22+||wd||22)
其中，μμ是正则化参数，LL是负对数似然：
L(wc,wd)=−∑i,yi=1logp(xi)+logλ(xi)−λ(xi)diL(wc,wd)=−∑i,yi=1logp(xi)+logλ(xi)−λ(xi)di
−∑i,yi=0log[1−p(xi)+p(xi)exp(−λ(xi)ei)] −∑i,yi=0log[1−p(xi)+p(xi)exp(−λ(xi)ei)]
该优化问题是无约束且二次可微的，本文使用L-BFGS进行优化，可参考：优化算法——拟牛顿法之L-BFGS算法
Tips
这篇文章的主要贡献：首次对延时反馈进行建模！
数据集：http://labs.criteo.com/tag/dataset
评价指标：平均负对数似然NLL
参数设置：μ:=1n||xi||22
————————————————
版权声明：本文为CSDN博主「南阁风起」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/qq_27465499/article/details/80085503